1. Introduction

This paper is an extension of a work originally presented at the International conference on electrical machines, drives and power systems “ELMA’17” [1].

Dielectric-barrier discharges (DBD) have been known for more than a century – the first experimental investigations focused on ozone generation were reported by Werner von Siemens in 1857. In 1951, Werner Eisby founded his company Vetaphone on the patent of a new plasma surface technology, which he initially named E-treatment and later it was known worldwide as the Corona technology. In fact, Corona was a Dielectric-barrier discharge in air at atmospheric pressure. This high-frequency electric discharge was controlled by a dielectric barrier and organized in the micro-discharge mode – it created a pattern of streamers distributed over the whole surface. This atmospheric pressure air-plasma (APP) pre-treatment was necessary to obtain sufficient wetting and adhesion on plastic films or metallic foils before high-speed roll-to-roll converting processes to ensure perfect surface finishing – printing, laminating or coating. Adding a Corona treater on a blown film or cast film extrusion line was essential in order to obtain a perfect surface free energy (SFE) prior to the following converting process. This plasma-aided finishing has proved to be both highly effective, cost-effective and can take place in-line [2, 3].

At the beginning of this century, the APP-activation (APPA) was used to enhance the wood finishing. In wood manufacturing finishing refers to the process of refining or protecting wooden surfaces. Wood finishing is the final step of the manufacturing process that gives wood surfaces desirable characteristics, including enhanced appearance and increased resistance to moisture, to fire and to attack from destructive organisms such as fungi and insects. It is well known that the inactivated by hydrophobic contamination wood surface has low SFE. This wood inactivation, [5], leads to poor wetting, adhesion, and impregnation especially for water-based varnishes and printing inks, adhesives and coating substances, as well as flame retardant water solution. The plasma-aided finishing has proved to be both highly effective, cost-effective, [6, 7], and can take place not only in-line, but mostly out-of-the-line. The three-dimensional wooden buildings and structures require removal of the plasma-aided finishing “in situ” out of the production line [8].In the 80s of the last century, the APP pre-activation came to facilitate the textile finishing. In textile manufacturing finishing refers to the processes, that convert the woven, non-woven or knitted cloth into a usable material or fabric to improve the aesthetic appearance and the functional characteristics of the finish textile. This plasma-aided finishing has proved to be both highly effective, cost-effective and can take place not only in-line, but also out-of-the-line. The finish textiles such as carpets, rugs, mats, curtains or clothing require the implementation of plasma-aided finishing out of the production line [3, 4].

The APPA is essential in surface finishing processes. Without plasma-chemical surface pre-treatment, the porous and non-porous substrates will not allow further finishing processes due to the low SFE. The plasma surface activation and functionalization are able to ensure that perfect finishing result we all want to see when looking at finish products. The objective of this kind of activation is to increase the SFE and subsequently the wettability, adhesion and wicking for laminating, printing, dyeing, gluing, impregnating and other finishing processes [9, 10].

Established APPA processes, such as plasma or flame activation, increase the SFE and decrease the contact angle, and therefore improve the processing characteristics. The Sessile Drop Test – a contact angle measurement technique, and the Dine Test – an ink test technique, were two widely used methods for SFE assessment and therefore for checking the need for APPA or the efficiency of such a pre-treatment processes [11, 12, 13].

The SFE of a solid cannot be measured directly because solids typically show no reaction to the exertion of SFE. Plasma, corona or flame treated and untreated surfaces are indistinguishable to the naked eye. Consequently, practical measurements of SFE involve the interaction of the solid with a test liquid to determine wetting surface tension as a measure of SFE. Standards such as DIN EN 828: 2013-04 (E) for adhesive finishing specify contact angle measurement as a method for determining the SFE of surfaces for checking the efficiency of cleaning or activating plasma pre-treatment processes.

The purpose of this paper is not only to collect new evidence and extend knowledge about the plasma-aided porous media finishing, especially capillary impregnation, with phosphorous flame retardant (FR) containing water solution for flame retardancy as finishing for wood, wooden and cellulosic materials, but also to provide a process efficiency assessment for the overall plasma enhanced process, not only for the APPA pre-treatment.

2. Assessment of plasma-activated finishing efficiency

2.1.  Model of wetting-wicking theory and efficiency assessment

Plasma-aided technique was used to facilitate the surface finishing, more precisely the surface impregnation of porous media such as wood, wooden and cellulosic materials [1, 14-17].

Porous materials with low SFE (σ_S) were subjected to plasma-chemical surface pre-activation for increasing their SFE and enhance the finishing. The wetting phenomenon occurs in a different way on porous media. The surface curvature of a sessile liquid drop on a porous solid depends not only on wetting but also on wicking in depth. This is a phenomenon of wetting-wicking. Wicking and wetting are essential in porous media finishing, such as capillary impregnation for flame retardancy of wood, wooden materials,woven and non-woven textile Figure 1, [1].

Both wetting and wicking together determine the variation of the sessile drop curvature and the contact angle over time. This is the wetting-wicking and contact angle phenomenon. That is why it is imperative in thе case of porous media to talk about apparent contact angle and apparent surface free energy. This process of contact angle change ends with the complete absorption of the flame retardant solution at almost constant value of the contact angle – end contact angle, much lower than the initial contact angle, Figure 2.

The “wetting-wicking theory”, expressed in terms of the thermodynamic parameters, such as the contact angle, the surface tension, and the surface free energy, can be the most widely used approach to porous media in wetting science at future, also referred here as “wetting-wicking phenomena”. Wetting-wicking is defined here as the ratio between the surface energies of the solid and the surface tension of the liquid [14].

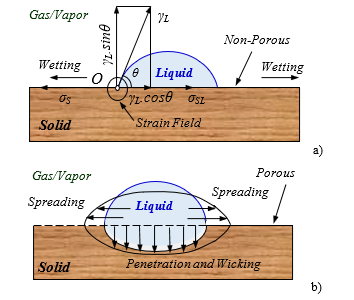Fig.1: Schematic illustration of two types of wetting phenomena: a) the wetting phenomenon on a non-porous surface when a liquid drop is placed on a smooth, non-porous and rigid solid, both exposed to gas/vapor, the system will not be in equilibrium and the liquid “wets out” or spreads over the solid, then the liquid exhibits a contact angle of zero against the solid (Good, 1993); b) the wetting-wicking or shortly wicking phenomenon on a porous surface can involve: i – spreading over the solid; ii – penetration or wicking into the porous solid (Berg, 1993).

According to Young’s equation, which is proven since over 200 years (1805), there is a fundamental relationship between the contact angle θ, deg, the surface free energy (SFE) of the solid σ_S, mJ/m², the surface tension (SFT) of the liquid γ_L, mN/m, and the interfacial tension (IFT) σ_SL between liquid and non-porous or porous solid, mJ/m², Figure 1a, [1, 15]:

                                    s_S – s_SL – γ_L cos θ = 0;                               (1)

                                    Σ = γ_L cos θ = σ_S – σ_SL,                               (2)

where Σ is the adhesion tension, mJ/m²; the adhesion tension reaches its maximum value at full wetting surface when the IFT reaches its minimum value: cos θ = 1 (θ = 0°); σ_SL = σ_S – γ_L; and Σ = γ_L.

The liquid in porous materials is often pulled into surface pores and capillaries by capillary action. The capillary action or capillarity is defined as the movement of liquid within the spaces of a porous media due to the forces of adhesion, cohesion and surface tension. Capillarity manifests itself when the adhesion to the capillary walls is stronger than the cohesive forces between the liquid molecules. Its ability to fill-in defects, such as surface-breaking cracks, voids, pores and capillaries can be imputed to a great extent to penetration, sorption or wicking characteristics. In porous media, capillary pressure p_C is the force necessary to squeeze a droplet through a pore throat and to work against the IFT between solid and liquid phases. Capillary pressure p_C is proportional to the adhesion tension Σ and depends only on it at a certain characteristic pore size r [16]:

                                  p_C = 2 (σ_S – σ_SL)/r = 2 Σ/r,                               (3)

where the capillary pressure p_C reaches its maximum value when the adhesion tension Σ reaches its maximum value at complete wetting: cos θ = 1 (θ = 0°); Σ = γ_L; and p_C = 2 γ_L/r.

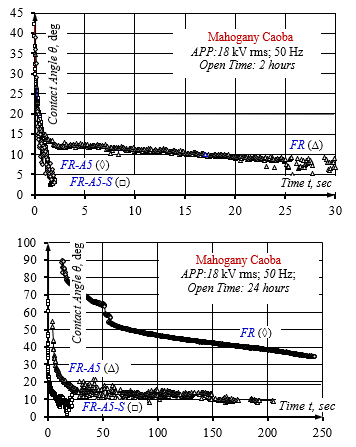Fig.2: Dynamics of change in apparent contact angle θ over time t depending on the used impregnating water solutions of phosphorous flame retardant with different surface tension: FR – 46.4 mN/m; FR-A5 – 22.4 mN/m and FR-A5-S – 18.5 mN/m, and short and long aging time, 2 or 24 hours.

Sessile and pendant drop analyses allow SFE and SFT to be quantified and to propose two distinct relationships that illustrate in general this process in the wetting area, θ Î [0÷90]° , – the IFE and adhesion tension Σ – proportional to capillary tension p_C, as a functions of the contact angle θ, Figure 3.

2.2.  The best solution rule for finishing and plasma-aided finishing efficiency parameter

Both SFE and SFT are essential in porous media finishing phenomena, (1). APPA surface technique can be used to enhance surface finishing: materials with low SFE were subjected to oxidative APPA to increase it, Figure 3.

The difference between SFE of porous surface and SFT of impregnating solution was chosen as a finishing efficiency or penetration-spreading parameter (PSP) for a real porous solid such as wood: PSP = (σ_S – γ_L). Finishing does not include evaporation of solution, dissolution or swelling of the solid by the water solution or any kind of chemical reaction between the solution and the solid substrate that changes the system composition. The higher the SFE of the solid, the better the finishing; the lower the SFT, the better the result of finishing. To sum up, large and positive difference between SFE and SFT: σ_S – γ_L > 0, (or σ_S > γ_L), will provide more effective porous surface finishing [1].

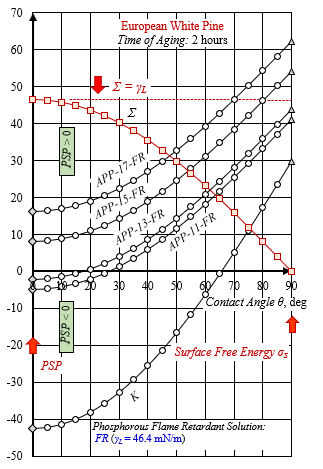Fig.3: Relationship between the “solid-liquid” interfacial energy σ_SL and the contact angle θ, measured by Sessile drop technique. Penetration-spreading parameter (PSP) is equal to the minimum IFE value at cos θ = 1 (θ = 0 °): PSP = min σ_SL. An effective finishing has a positive value of PSP: PSP > 0; a non-effective finishing has a value of less than or equal to zero: PSP ≤ 0. Surface free energy σ_S is equal to maximum IFE value at cos θ = 0 (θ = 90 °): σ_S = max σ_SL.

Relationship between the adhesion tension Σ and the contact angle θ. The maximum adhesion tension Σ value is equal to the surface tension γ_L of the flame retardant water solution FR: γ_L = 46.4 mJ/m².

Atmospheric pressure plasma pre-activation at 50/60 Hz and different voltage: 11, 13, 15 and 17 kV rms: method – in situ; time of activation – 60 sec; glass barrier – 3 mm; air gap – 6 mm.

In general, the following processing efficiency parameter was found and the rule is true: “The plasma aided or enhanced finishing of a porous media will be more successful and this media will be more susceptible to it as the difference between its SFE σ_S and the SFT γ_L or the so-called penetration-spreading parameter is positive: PSP = (σ_S – γ_L) > 0. If not, wetting, wicking and finishing problems will occur” [1].

This new rule of processing efficiency is fully consistent with the well-known rule formulation: “If the liquid has a dyne level (SFT) lower than the substrate dyne level (SFE), γ_L < σ_S, then the liquid will spread out over its entire surface in uniform wet layer. If the liquid dyne level is equal to or higher than a substrate dyne level, γ_L ≥ σ_S, the liquid will become cohesive and tend to remain in droplets” [18]:

                              σ_S > γ_L: σ_S – γ_L > 0 or PSP > 0.            (4)

According to Young’s equation, there is a fundamental relationship between IFE and PSP = (σ_S – γ_L):

         σ_SL = (σ_S – γ_L) + γ_L (1 – cos θ) = PSP + γ_L – γ_L cos θ;    (5)

                 min σ_SL = (σ_S – γ_L) = PSP; θ = 0°: cos θ = 1,            (6)

or the minimum value of the “solid-liquid” IFE at θ = 0° is equal to the value of PSP: σ_SL = PSP, Figure 3, [1, 14].

Table 1. Contact angle, wetting and hydrophilicity change.

Contact angle θ, °	0	10	20	30	70	90
cos θ	1	1 > cos θ > 0				0
Interface free energy (IFE)	σSL= PSP					σSL = σS
Hydrophilicity / Hydrophobicity	Hydrophilicity				Hydro phobicity
	Super- Hydrophilicity		Hydro philicity		Hydro phobicity
Degree of wetting	Spreading	Complete wetting	Wetting	Partial wetting		Incomplete wetting
Wettability	High wettability

The maximum value of the IFE, at θ = 90°, is equal to the value of porous wood SFE: σ_SL = σ_S, Figures 3 and 4.

Therefore, the requirement for process efficiency finishing PSP = (σ_S – γ_L) > 0 can be transformed into a new requirement for effectiveness, Figure 3:

                                        σ_S > σ_SL > PSP > 0,                                     (7)

which already refers directly to IFE: “it is necessary for the entire range of variation of the static contact angle (0° ≤ θ ≤ 90°) in the area of the high wetting, the value of the IFE to be greater than zero: σ_SL > 0”.

Plasma-aided capillary impregnation finishing will be more successful and the porous media will be more susceptible when the PSP > 0. This is the essence of the rule for obtaining effective plasma-enhanced capillary impregnation finishing.

Surface activation refers to the temporal increase of the SFE determined by the rise of the polar part of the SFE, Figure 4. This APPA process is based on the implantation of oxygen, leading to the formation of functional groups like ether (C-O), hydroxyl (C‑OH), carbonyl (C=O), and carboxyl (O=C–OH). Such a plasma treatment enhances the affinity of the substrate for other substances and is especially needed for solids which typically have a low intrinsic SFE. This process is generally achieved using a standard DBD in open air and “in situ” or remote application Figure 5.

The PS-parameter depends only on two thermodynamic parameters of the finishing process – the SFE σ_S of the solid and the SFT γ_L of the liquid, which can be quantified individually using two well-known methods of contact angle measurement – the sessile drop and the pendant drop techniques [15, 16 and 17].

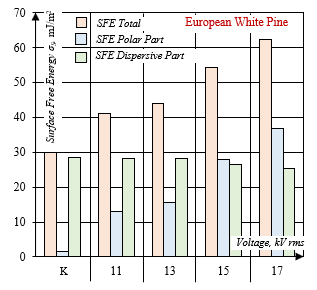Fig.4: Surface free energy σ_S and its dispersive and polar parts for European white pine after APPA and 2 hours of aging time and varied voltage: 11,13,15 and 17 kV rms, defined by Sessile drop technique and theory of Wu.

Working with the graphs and studying the relationship between the “solid-liquid” IFE σ_SL and contact angle θ in the area of high wettability, 0° ≤ θ ≤ 90°, it becomes clear that the graphs of the efficiency realizations of plasma-aided surface impregnation – APP-15-FR and APP-17-FR are located in the first quadrant above the abscissa, Figure 3.

One more graphic illustration has been brought about, Figure 5, depicting the efficiency parameter assessment of plasma-aided capillary impregnation with modified phosphorous FR solution by increasing the SFE and decreasing the SFT of the impregnating solution.

2.3.  Aging, plasma activation durability and open time

It is very important to realize that the changes induced on the surface by an APPA are not permanent. There is aging, which is the effect of the APPA or SFE decreasing in time. Often, the activation effect will remain partially and a steady state will be reached after some hours, days or weeks. For APPA, the aging can be really an issue. Hence the typical APPA was performed “in-line”, immediately before the finishing for which it is intended. Aging was usually regarded as an unwanted side-effect in plasma-aided finishing [17, 19].

The time of aging or open time is the period of time after an APPA has been applied, allowing for the finishing processes to take place – printing, bonding, painting, laminating and impregnating, during which an effective plasma-aided finishing can be achieved. Plasma pre-activation most often takes place “in-line” immediately prior to the onset of the finishing. The time of aging in this case is zero. The time of aging is different from zero when the plasma-aided capillary impregnation is applied “out-of- the-line”, for example in the finishing of a wooden building construction, wood paneling, flooring or staircase. Most often, the entire surface is activated “step by step” for a certain time and then it is proceeded to capillary impregnation, Figure 6.

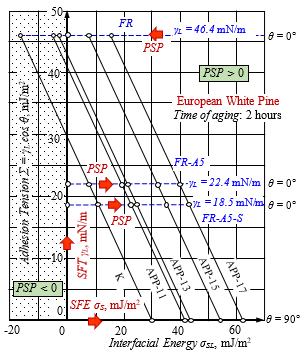Fig.5: Relationship between the adhesion tension Σ and the “solid-liquid” interfacial energy σ_SL that reveals at once the impact of: i – the variation of SFE as result of APPA and 2 hours of aging at varied voltage: 11, 13, 15 and 17 kV rms; ii – the variation of SFT as a result of FR-solution modification with surfactants: FR-A5 – with micelle-forming anionic surfactant at 5 vol. % and FR-A5-S – with trisiloxane surfactant at 0.1 vol. %.

The industrialization of the plasma-aided finishing “out-of-the- line” during 2007÷09 allowed the empirical definition of two very important values for the time of aging – 2 hours or a short time of aging, allowing for successful finishing of large-scale wood wares such as paneling, flooring, wooden construction, and a day or 24 hours, a long time of aging, which is close to the critical open time when the effect of the plasma activation will be obliterated.

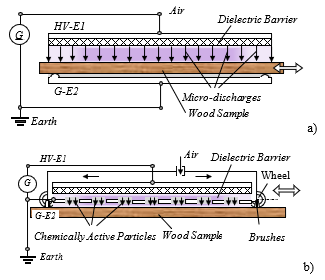Fig.6: Atmospheric pressure plasma pre-activation by dielectric barrier discharge in air: a) APPA, “in situ” activation where the sample is immersed in the cold plasma of the DBD (Eisby, 1951); b) RAPPA, remote activation where the sample interacts only with the chemically active particles produced by the DBD (P. Dineff, 2005).

HV-E1 – high-voltage electrode; G-E2 – grounded electrode; G – AC electric generator (50/60 Hz).

Remember that the SFE level decay is extremely fast right after APP-activation “in line” – in fact an immediate loss of 10 mJ/m² is possible. This is due to the contact with process rolls, surface migration of additives and interfacial transfers between treated and untreated surfaces within the finished wound roll. Generally, the SFE of a film should be between 3 and 10 mJ/m² greater than the SFT of the ink or impregnating liquid in order to ensure acceptable performance, Figure 6, [11, 18].

The highest plasma-activation effect to the finishing, expressed by maximum SFE value increase, was observed with “in situ” APPA, “in line” application, Figure 6, [1, 18].

The objective of this paper is to study the efficiency assessment of plasma-aided capillary impregnation as finishing for flame retardancy of wood at industrial frequency (50 Hz) and voltage of 15/18 kV rms, after short and long aging time, 2 and 24 hours, and the change of the wood impregnability monitored by the penetration-spreading parameter (PSP) and the processing efficiency rule: PSP > 0.

3.          Experimental investigation

The development of a plasma-enhanced capillary impregnation finishing for wood flame retardancy goes through three stages:

• The first stage includes the selection of an effective APPA mode that provides the necessary high level of SFE after a short aging of 2 hours, Figures 3 and 9;
• The second stage includes the selection of an anionic micelle-forming water surfactant in a concentration to ensure the required low level of the SFT: 30 mN/m > γ_L > 20 mN/m, Figure10;
• The third stage includes the selection of an effective APPA mode that will provide the necessary high level of SFE after a long time of aging, a day or 24 hours, and low level of SFT, by some adequate surfactants and concentrations, Figure 11.

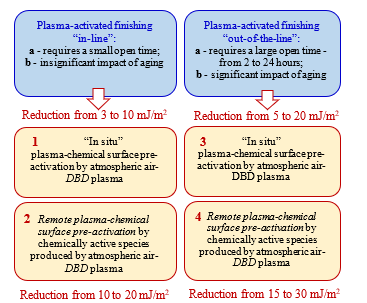Fig.7: Surface free energy reduction before finishing due to: i – contact with other non-activated surfaces, ii – aging after plasma activation, and iii – different modes of plasma surface activation provide different activation options: APPA, “in situ” activation immerced in cold plasma or RAPPA, remote activation with chemically active particles.

This experimental study was carried out on four kinds of wood samples: European white pine (Pinus Sylvestris L.) from Bulgaria and three woods from Mexican rain forest: Tzalam (Lysiloma Bahamensis L.), Mexican white cedar (Cupressus lusitaca L.), Mahogany caoba (Swietenia mahogany L.), according to the well-known method [1, 15-17]. The selected wood species form the following range of decreasing density, in kg/m³: Tzalam – 780; Mahogany caoba – 650; Mexican white cedar – 470; European white pine – 371. There are two hard wood species with high density, d > 540 kg/m³: Tzalam and Mahogany caoba, and two soft wood species with low density, d < 540 kg/m³: Mexican white cedar and European white pine.

On the basis of our own former experience in plasma-aided capillary impregnation of wood and wooden materials, [9-12], an oxidative APPA has been applied on the test samples for 60 sec. This study employs a well-known experimental methodology, already used by us [1, 14-17].

All experimental studies pertain to APPA of the wood specimens in a specific burning mode of the air DBD at atmospheric pressure (~ 101 kPa) at the first peak of surface density of real power p_a = 26 W/m² and the second peak p_a = 8 W/m² in asymmetric rectangular coplanar electrode system with 6 mm air gap – mode A and B respectively, Figure 7.

The APPA was carried out with “in situ” application of DBD for 60 sec, Figure 5a. The effective operating modes of DBD at voltages above 13 kV rms (18.3 kV peak value) determine a surface density of real power above 4 W/m², Figure 7.

The aim of this study was to verify the possibility to evaluate the PS– efficiency parameter values for plasma and surfactant enhanced capillary impregnation trough calculation of SFE and SFT by drop shape analysis. Drop shape analysis is an image analysis method for determining the contact angle from the shadow image of a sessile drop and the SFT from the shadow image of a pendant drop. There are number of theories and models for SFE calculation with the help of contact angle data. The method according to Wu for calculating SFE and its two parts – polar and disperse, is suitable for high polar or plasma activated surfaces, Figure 4.

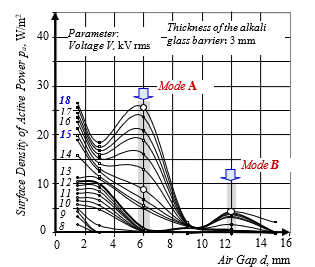Fig.8: Technological discharge characteristic “surface density of active power p_a – air gap size d” of non-equilibrium DBD burning at industrial frequency (50 Hz) in asymmetric rectangular coplanar electrode system with one glass barrier.

All methods described are included in the KRÜSS Drop shape analysis programs. Drop Shape Analyzer (DSA100 and DSA30, KRÜSS GmbH, Germany) was used for the precise measurement of contact angle SFE and also for measurement of the SFT of liquids using the pendant drop method. Measuring range (referred to image analysis) for Sessile drop technique: contact angle – 1°¸180°; surface free energy – 0.01¸1 000 mJ/m²; and for Pendant drop technique: surface tension – 0.01÷2000 mN/m. Measurement accuracy: contact angle – 0.3°; surface tension – 0.3 mN/m [7].

Modes of APPA for wood samples: mode A – cathode-directed streamer mode at air gap of 6 mm; mode B – anode-directed streamer mode at air gap of 12 mm, Figure 8.

A halogen-free, phosphorous and nitrogen containing flame retardant (FR) based on ortho-phosphorous acid, urea and ammonia has been produced and studied as water solution. The impregnating FR water solution was based on it: dry substance of 30 wt. %; phosphorus content of about 13 wt. %, pH = 7÷8 and density of 1.15÷1.14 g/cm³.

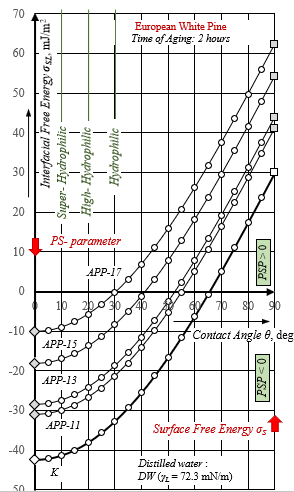Fig.9: The use of distilled water as a test-liquid with SFT – γ_L = 72.3 mN/m, does not carry adequate information on the efficiency of the finishing of FR capillary impregnation – no effective mode of APPA has been found at voltages up to 17 kV rms for European white pine: PSP= σ_S – γ_L < 0. All SFE values were determined according to the method of Wu for short aging time of two hours.

The non-equilibrium air (oxidative) APPA was combined with anionic micelle-forming (AS, “Anticrystalin A”, Chimatech, Ltd., Bulgaria) and trisiloxane-ethoxylate surfactant (Y-17113, Momentive Performance Materials GmbH & Co. KG, Germany) enhanced capillary impregnation with well-known experimental methodology [10, 11, 12].

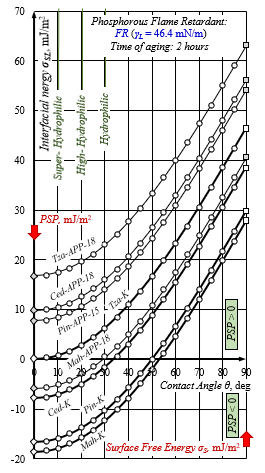Fig.10: Effective mode selection of APPA at an air gap of 6 mm and short aging time of two hours for plasma-aided capillary impregnation finishing was found only for European white pine (Pin-LF-15), Mexican white cedar (Ced-LF-18), and Tzalam (Tza-LF-18): PSP> 0. No steady APPA mode for Mahogany caoba (Mah-LF-18) was found: PSP = 0.1 mJ/m² ≈ 0. Plasma pre-activation modes provided trought the declared voltage – 15/18 kV rms, get the maximum SFE value for each species of studied woods.

4.          Experimental rezults and discusion

This study meets another issue which can be formulated as follows: “is it possible a simple drop test with distilled water (DW) to adequately replace the entire PSP study conducted with a real impregnating FR-water solution”.

The answer can be found in the information provided in Figure 3 and 8. The use of distilled water as a test-liquid does not carry adequate efficiency assessment of the finishing – the plasma-aided capillary impregnation. The effective mode selection (APP-XX: APPA at 11, 13, 15, and 17 kV rms; 50/60 Hz) can be determined only by the use of FR solution – a basic FR water solution containing phosphor- and nitrogen flame retardant with SFT, γ_L = 46.4 < 72.3 mN/m, and the relationship between the “solid-liquid” IFE (σ_SL) and static contact angle θ measured by Sessile drop technique – IFE acquires a value equal to the PS-Parameter at complete wetting, i.е. contact angle equal to zero: σ_SL = PSP

 (θ = 0).

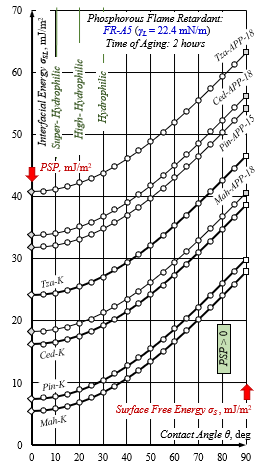Fig.11: Effective mode selection of APPA at an air gap of 6 mm and short aging time of two hours for plasma-aided capillary impregnation finishing was found for all wood species by decreasing the SFT of the basic phosphoric FR solution with anionic micelle-forming water surfactant at 5 vol. % (FR-A5): γ_L = 22.4 mN/m. The rule of processing efficiency was met for all applications of capillary impregnation – non-activated (-K) and APP-activated (-APP-XX) at different voltages: 11, 13, 15 and 17 kV rms: PSP > 0.

Distilled water has a too high SFT: γ_L = 72.3 > 46.4 >> 22.4 mJ/m². APPA cannot compensate it by increasing SFE, so a rule process efficiency should be enforced: σ_S < γ_L; PSP < 0, Figure 8. Normally, it fails to predict the efficiency of the plasma-aided finishing with modified γ_L = 22.4 mJ/m², or non-modified γ_L = 46.4 mJ/m², FR-solution, Figures 3 and 8.

All modes of APPA with a voltage higher than 13 kV rms (18.3 kV peak value) provide processing efficiency finishing of capillary impregnation: PSP > 0, Figure 3.

At the first stage, the PSP- testing indicates that the voltage of the APPA for European white pine samples should be 15 kV rms (σ_S = 54.2 kJ/m²) for a maximum processing efficiency of the FR (γ_L = 46.4 mJ/m²) impregnation finishing: max PSP = 7.8 mJ/m²

> 0, Figure 9.

The most effective voltage for the other studied species of wood was determined using the same procedure and it is 18 kV rms. They are arranged in order of decreasing PS-parameter according to their density, mJ/m²: Tzalam – 16.78, Mexican white cedar – 9.8 and European white pine – 7.8. However, no steady APPA mode for Mahogany caoba was found: PSP = 0.1 mJ/m²

≈ 0. This result indicates that there are wood species for which a processing efficiency finishing – a capillary impregnation, cannot be applied, Figure 9.

At the second stage, the PSP– testing of the all studied wood species indicates that the modified FR– solution with less SFT  γ_L = 22.4 mJ/m², performs the rule of processing efficiency after a short time of aging, PSP > 0, Figure 10.

At the third stage, the PSP– testing of all studied wood samples indicates that the APPA and the finishing of capillary impregnation with the modified impregnating FR solution (FR-A5), γ_L = 22.4 mJ/m², satisfy the rule of finishing processing efficiency: PSP > 0, Figure 11.

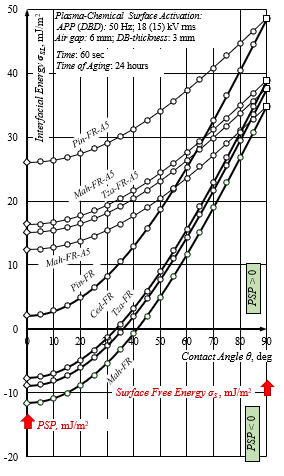Fig.12: Effective mode of APPA at air gap of 6 mm and short and long aging time – 2 and 24 hours, for plasma-aided capillary impregnation finishing was found for all studed wood samples by decreasing the SFT of the FR impregnating solution with anionic micelle-forming surfactant at 5 vol. % (-FR-A5): γ_L = 22.4 mN/m. The rule of processing efficiency was met for all applications of plasma-aided finishing with this modified solution: PSP> 0.

This study proves our claim that the plasma-aided capillary impregnation can be applied “out-of-the-process-line” after a long time of aging 24 hours, between APPA and the capillary impregnation finishing.

The plasma-aided capillary impregnation of porous woods has resulted in the formation of a FR-functional coating with a certain thickness, continuity and defect-free surface. In porous media, the capillary pressure p_C is proportional to the adhesion tension Σ and depends only on it at certain characteristic pore size, (3).

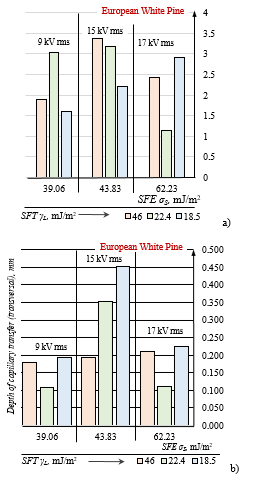Fig.13: Effect of APPA mode (voltage) – 9, 15 and 17 kV rms (50/60 Hz; air gap: 6 mm), the short time of aging – 2 hours, the used impregnating phosphorous FR solutions and consumption rate – constant rate: 0.139 l/m² (dm³/m²) on the depth of “capillary” transfer to the wood capillary direction: longitudinal – capillary displacement (a) and transversal – wicking through the capillary walls (b). The best quality of the plasma-aided capillary impregnation for flame retardancy of European white pine is at 15 kV rms.

It was expected that the largest DBD voltage of 17 kV rms should ensure greater depth of wicking transfer as the SFE and its greatest polar part, which determines greater value of PS– efficiency parameter. Although the SFE and its polar part are greater, Figure 4, just like the PS-parameter, Figure 3, the depth of capillary transfer – longitudinal to the capillary structure and transversal to it, or through the capillary walls, is less than 15 kV rms, Figure 12. What is typical for this mode (15 kV rms) of plasma and surfactant enhanced capillary impregnation, is that the polar part of the SFE becomes greater than the dispersive part of SFE, Figure 4. The transition to more intensive mode of APPA (17 kV rms) does not give a positive result in spite of increasing SFE and its polar part, and PS-efficiency parameter.

Both the capillary displacement and the wicking through the capillary walls are two visible forms of maximum solution transfer, Figure 12. The maximum capillary displacement was determined by a maximum value of capillary pressure p_C or adhesion tension Σ respectively. This is determined by the maximum basic FR solution, Figure 5 and 13. On the contrary, the maximum wicking through the capillary walls was obtained at the minimum value of adhesion tension Σ; this is provided by the modified FR-A5-S solution. Wicking, however, is essential for the impregnation process. More extensive studies on different species of wood are needed to confirm this experimental fact, which has been observed only for European white pines so far.

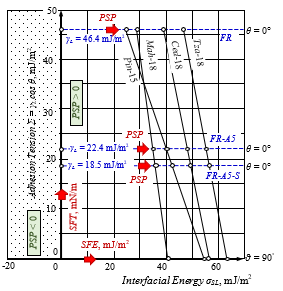Fig.14: Relationship between the adhesion tension Σ and the “solid-liquid” interfacial energy σ_SL that reveals at once the impact of: i – the variation of SFE as result of APPA at short time of aging (2 hours), air gap of 6 mm and voltage 15 kV rms; ii – the variation of SFT as a result of FR-solution modification with surfactants: FR-A5 – anionic micelle-forming surfactant at 5 vol. %; FR-A5-S – trisiloxane neutral surfactant at 0.1 vol. %.

In conclusion, an attention has to be paid to the fact that the transfer of the FR-solution in depth is mainly carried out in the more complicated way through the capillary walls. The modification of the basic FR-solution through the combination of anionic micelle-forming and trisiloxane surfactant thus acquires a new meaning.

The graphical representation of the relationship between adhesion tension Σ and “solid-liquid” IFE σ_SL fully illustrates the two pathways for achieving the finishing efficiency PSP of plasma-aided capillary impregnation by increasing the SFE of porous media and reducing the SFT of the impregnating FR solution, Figures 5 and 13.

By selecting the voltage, the quality of the APPA expressed by the process efficiency parameter PSP was controlled: the SFE of the European white pine samples was increased; the SFT of the impregnating FR solution was decreased. The process efficiency parameter PSP meets the rule of plasma-aided finishing efficiency, PSP > 0, at and above 15 kV rms, Figure 5. For all wood species, the maximum process efficiency parameter PSP is at a voltage of 18 kV rms, Figure 13.

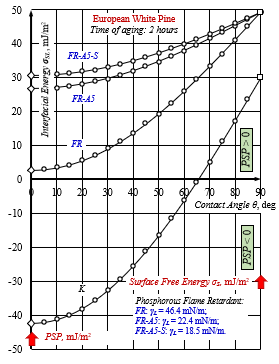Fig.15: Effective mode selection of plasma-aided capillary finishing of European white pine after two hours aging time from air RAPPA at air gap of 6 mm by a modification of the phosphoric FR-solution with an anionic micelle-forming water surfactant at 5 vol. % (FR-A5) and neutral trisiloxane surfactant at 0.1 vol. %. The rule of processing efficiency was met for all plasma-aided applications of capillary impregnation.

The new created plasma-aided finishing can find its wide application only if it can be envisaged and managed so as to observe the process efficiency rule: PSP > 0, Figure 15.

The prerequisite for this is the possibility for SFE measurement “in situ” out of the lab. We believe that this approach can be successful, as the market now has a technical device for measuring the SFE “in situ” – pocket goniometers, mobile or hand-held surface and contact angle analyzers.

There is also an innovative “mobile” analyzer with two test liquids using a dispenser with two parallel drops with “one click” for direct analysis of the static contact angles and the results obtained from the SFE.

Conclusion

Plasma, surfactant or plasma and surfactant aided finishing were used to enhance the finishing of capillary impregnation and thus the flame retardancy of wood: wood materials and constructions – timber, lumber, plywood, cardboard, paper, flooring, paneling, staircase and wooden structure with low SFE were subjected to APPA and RAPPA for increasing their SFE.

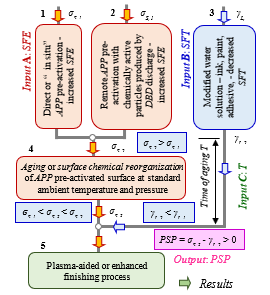Fig.16: Schematic representation of the plasma-aided impregnation finishing model – flow of information and processes involved in the processing efficiency and results to be obtained. Management of the plasma-aided finishing with two input factors – SFE of the porous solid and SFT of the liquid. The time of aging is set depending on the APPA and impregnation used technology.

In general, a processing efficiency parameter named PSP was found: “Plasma, surfactant or plasma and surfactant enhanced finishing of capillary impregnation will be more successful and the material will be more susceptible when the PSP is positive: PS > 0”.

This process efficiency parameter was defined by the difference between the SFE of the porous wood and the SFT of the impregnation FR– solution: PS = σ_S – γ_L. This efficiency parameter is equal to the value that gets the IFE when the water solution wets the surface completely: PS = σ_SL, θ = 0° (cos θ = 1).

The efficiency of a plasma-aided impregnation finishing can be predicted only by setting both basic parameters of the real porous wood surface and the actual FR-impregnating solution – the SFE and the SFT. Successful plasma aided or enhanced finishing, including the capillary impregnation, can be expected if the process efficiency parameter takes a positive value, PSP > 0, after a prescribed aging time – 2 or 24 hours.

The evolution of plasma-enhanced wicking phenomena in time after APPA – the short and long-time aging of plasma activated surface, after 2 and 24 hours, was investigated for four species of wood by the PS-efficiency parameter change. All species of wood were ranked according to the plasma aided capillary impregnation process efficiency as per its PSP.

The existing methods and instruments for measuring the SFE of solids and SFT of liquids, including portable measurement systems, [20], allow this approach to determine the process efficiency of the plasma-enhanced finishing such as impregnation, printing, painting, laminating to be recommended for application “in-line” and “out-of-the-line”.

1. Dineff, P.; Gospodinova, D.; Ivanov, I. Processing efficiency of plasma-aided porous media finishing. Prossidings of the 15-th international conference on electrical machines, drives and power systems (ELMA), IEEE 2017, IEEE Part Number CFP17L07-ART, pp 334-338.
2. Fridman, A. Plasma chemistry. Cambridge University Press, Cambridge, England, New York; 2008.
3. Plasma technologies for textiles. Edited by Shishoo, R. Published by Woodhead Publishing Limited, Abington, Cambridge, England, 2007.
4. Plasma Technology for Hyperfunctional Surfaces. Food, Biomedical and Textile Application, Edited by Rauscher, H.; Perucca, M.; Buyle, G. WILEY-VCH Verlag GmbH & Co., Weinheim Germany, 2010.
5. Sernek, M. Comparative analysis of inactivated wood surfaces. Doctoral thesis, 2002. Glasser, W.; Kamke, F. (Co-Chairs). Virginia Polytechnic Institute and State University. Blacksburg, Virginia, USA.
6. Viöl, W. Method for modifying wooden surfaces by electrical discharges at atmospheric pressure. WO039944A1 (EP1233854B1; US6818102). Priority Date: 01.12.1999; Publication Date: 16.11. 2004.
7. Cernak, M.; Rahel, J. Apparatus and method for treatment of wood, wood fibres and wood-based materials. WO Patent WO2008085139A1 (EP2095694A1), Priority date: 05.12.2006; Publication date: 17.07.2008.
8. Dineff, P.; Kostova, L. Method for plasma chemical surface modification. WO Patent WO2006133524A2 (BG 66022B1); Priority Date: 14.06.2005; Publication date: 12.04.2007.
9. Podgorski, L.; Chevet, B.; Onic, L.; Merlin, A. Modification of wood wettability by plasma and corona treatments. J. Adhes. Adhes 2000, 20(2), pp 103÷111. Doi: 10.1016/S0143-7496(99)00043-3.
10. Avramidis, G.; Wascher, R.; Militz, H.; Viöl, W. Impact of air-plasma treatment at atmospheric pressure on wood and wood extractives. Int. Wood P. 2016. 7(2) pp 76-79. 8-th European Conference on Wood Modification. Doi: 10.1080/20426445.2016.1162429.
11. Nolan, M. Dyne testing –why test in the first place? Converting Supply, Inc., Ontario, Canada, 2011.
12. Why test inks cannot tell the full truth about surface free energy. Application report No 272, Krüss GmbH, Hamburg Germany, 2014. kruss.de.
13. Wolkenhauer, A.; Avramidis, G.; Militz, H.; Viöl, W. Plasma treatment of heat treated beech wood – investigation on surface free energy. Holzforschung 2008. 62(4), pp 472-474. Doi: 10.1515/HF.2008.074.
14. Dineff, P.; Gospodinova, D.; Ivanov, I. Study on processing efficiency of plasma-aided capillary impregnation of porous media through a penetration-spreading parameter. Porceedings of the X-th international conference advanced manufacturing technologies & XI-th international conference advanced materials and operations (AMT&AMO 2016). 2016, pp 54-65.
15. Dineff, P.; Ivanov, I.; Gospodinova, D. Efficiency processing parameter for plasma-aided surface impregnation: I. Penetration-spreading parameter. 19-th international symposium on electrical apparatus (SIELA) 2016. IEEE DOI: 10.1109/SIELA.2016. 7542991.
16. Dineff, P.; Ivanov, I.; D. Gospodinova, “Efficiency Processing Parameter for Plasma-Aided Surface Impregnation: II. Interfacial Energy, Adhesion and Capillary Pressure. 19-th international symposium on electrical apparatus (SIELA) 2016; IEEE DOI: 10.1109/SIELA.2016.7542992.
17. Dineff, P.; Ivanov, I.; Gospodinova, D.; Stanimirova, R. Efficiency Processing Parameter for Plasma-Aided Surface Impregnation: III. Plasma Surface Activation. 19-th international symposium on electrical apparatus (SIELA) 2016; IEEE DOI: 10.1109/SIELA.2016.7542993.
18. Corona and plasma for extrusion. Vetaphone A/S, Denmark, 2017. vetaphone.com.
19. Wolkenhauer, A., Avramidis, G.; Hauswald, E.; Militz, H., Viöl, W. Sanding vs. plasma treatment of aged wood: a comparison with respect to surface energy. Intern. J. Adhes. Adhes. 2009. 29(1), pp 18-22. Doi: 10.1016/j.ijadhadh.2007.11.001.
20. Mobile surface anlyzer – MSA. Krüss GmbH, 2017. kruss.de.

(Click to view)

(Click to view)