1. Introduction

This paper is an extension of work originally presented in ICMSAO2017 [1] and covers the author’s study on a few isomorphic properties of circulant graphs that includes (i) Existence of selfcomplementary circulant graphs; (ii) Type-2 isomorphism, a new type of isomorphism other than already known Adam’s isomorphism of circulant graphs that helps to obtain graphs without CI-property and abelian groups and (iii) Cartesian product and factorization of circulant graphs similar to the theory of product and factorization of natural numbers.

Beauty comes out of symmetry as well as asymmetry. Investigation of symmetries/asymmetries of structures yield powerful results in Mathematics. Circulant graphs form a class of highly symmetric mathematical (graphical) structures. In 1846 Catalan (cf. [2]) introduced circulant matrices and properties of circulant graphs have been investigated by many authors [1-20]. An excellent account of circulant matrices can be found in the book by Davis [2] and circulant graphs in the article [11].

If a graph G is circulant, then its adjacency matrix A(G) is circulant. It follows that if the first row of the adjacency matrix of a circulant graph is [a₁,a₂,…,a_n], then a₁ = 0 and a_i = a_n−i+2, 2 ≤ i ≤ n [15, 17].

Through-out this paper, for a set R = {r₁,r₂,…,r_k}, C_n(R) denotes circulant graph C_n(r₁,r₂,…,r_k) where

. Only connected circu-

lant graphs of finite order are considered, V (C_n(R)) = {v₀,v₁,v₂,…,v_n−₁} with v_i adjacent to v_i+r for each r ∈ R, subscript addition taken modulo n and all cycles have length at least 3, unless otherwise specified, 0 ≤ i ≤ n − 1. However when R, edge v_iv_i+n2 is taken as a single edge for considering the degree of the vertex v_i or v_i+n2 and as a double edge while counting the number of edges or cycles in C_n(R), 0 ≤ i ≤ n − 1. Generally, write C_n for C_n(1) and j

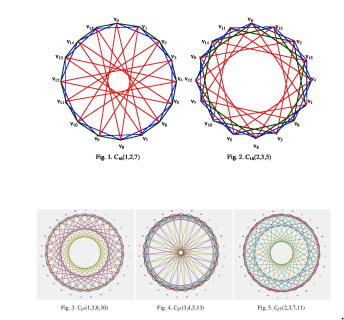
C_n(1,2,…,) for K_n. We will often assume, with-out further comment, that the vertices are the corners of a regular n − gon, labeled clockwise. Circulant graphs C₁₆(1,2,7), C₁₆(2,3,5), C₂₇(1,3,8,10),C₂₇(3,4,5,13) and C₂₇(2,3,7,11) are shown in Figures 1 – 5. Now, let us consider the following definitions and results that are useful in the subsequent sections.

Definition 1.1. [17] Let n and r be positive integers with n ≥ 4 and r < ⁿ₂. Then, clearly, C_n(r) consists of a collection of cycles (v₀v_rv_2r …v₀), (v₁v_1+rv_1+2r …v₁), …, (v_r−1v₂r−1v₃r−1…v_r−1). If d = gcd(n,r), then there are d such disjoint cycles, each of length _dⁿ. We say that each of these cycles is of period r, length _dⁿ and rotation _d^r .

If r = ⁿ₂, then obviously C_n(r) is just a 1 − f actor. Since C_n(R) is just the union of the cycles C_n(r) for r ∈ R, we have a decomposition of C_n(R).

Theorem 1.2. [17] Let r ∈ R. Then, in C_n(R), the length of a cycle of period r is _gcdⁿ_(n,r) and the number of disjoint periodic cycles of period r is gcd(n,r).

Corollary 1.3. [17] In C_n(R), the length of a cycle of period r is n if and only if gcd(n,r) = 1, r ∈ R.

Remark 1.4. [17] Let |R| = k. Then, the circulant graph C_n(R) for a set R = {r₁,r₂,…,r_k} is (2k−1)−regular if  R and 2k − regular otherwise.

The following Lemmas are useful to obtain one-toone mappings.

Lemma 1.5. [15] Let A and B be two non-empty sets. Let f : A → B be a mapping. Then, f is one-to-one if and

only if f /_A⁰ is one-to-one for every non-empty subset A⁰ of A.

Lemma 1.6. [15] Let A and B be non-empty sets and A₁,A₂,…,A_k be a partition of A (each A_i being nonempty, i = 1,2,…,k). Let f : A → B be a mapping. Then f is one-to-one if and only if f /_Ai is one-to-one for every i, i = 1,2,…,k.

2. On self-complementary circulant graphs

In 1962, Horst Sachs [14] proved that the sufficient condition for the existence of a self-complementary circulant graph of order n is that every prime factor p of n should satisfy p ≡ 1 (mod 4). He also conjectured that the sufficient condition is a necessary one. We have proved that the self-complementary circulant graph on n vertices does not exist if n has any prime factor which is not of the form 4m + 1, m ∈ _N. Thereby, we establish that the sufficient condition is also a necessary one. The proof is based on counting the number of disjoint cycles of a particular length in K_n and is given in this section [4, 17]. Graphs given in Figures 6 and 7 are self-complementary but not of circulant whereas graphs given in Figures 8 and 9 are self-complementary circulant graphs.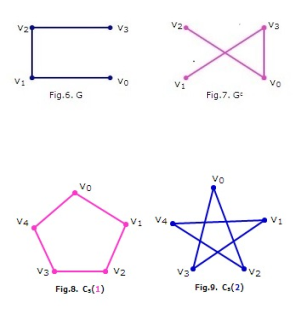

Theorem 2.1. [17] If C_n(R)  C_n(S), then there is a bijection f from R to S so that for all r ∈ R, gcd(n,r) = gcd(n,f (r)).

Proof.                     The proof is by induction on the order of

Theorem 2.2. [9] If graph G of order n is selfcomplementary, then n ≡ 0,1 (mod 4).

Theorem 2.3. [17] If C_n(R) for a set R = {r₁,r₂,…,r_k} is self-complementary, then n ≡ 1 (mod 4).

Proof. Using Theorem 2.2, we get n ≡ 0,1 (mod 4). When n is even, a circulant graph is of even degree if and only if its complement is of odd degree since any circulant graph is a regular graph. Thus, selfcomplementary circulant graph of even order doesn’t exist. Hence, we get the result.

Theorem 2.4. [17] If C_n(R) for a set R = {r₁, r₂, …, r_k} is

self-complementary, then n = 4m + 1, k = m and |S_i| is even where S_i ,

h for all i, i = 1,2,…,.

Proof. Using Theorem 2.3, we get, n = 4m + 1. This implies that the degree (of each vertex) of a selfcomplementary circulant graph of order 4m +1 is 2m which implies k = m.

Let C_4m+1(R) be a self-complementary circulant graph for R = {r₁, r₂, …, r_m}. If it contains a cycle of period r (and of length _gcdⁿ_(n,r), using Theorem 1.2), then its complement also contains a periodic cycle of period, say, s such that gcdn(n,s) = gcdn(n,r), ⁱ, using Theorem 1.2. This implies that gcd(n,s) = gcd(n,r). Here we consider that the cycles of periods r_i and n − r_i are the same in C_n(r₁,r₂,…,r_k), 1 ≤ i ≤ k. Combining the above arguments, we get the result.

Remark 2.5. The above theorem states that if a selfcomplementary circulant graph of order n exists, then n = 4m + 1 and so it is 2m-regular and the number of periodic cycles of length i in K_n is always even for each i,

Theorem 2.6. [17] Self-complementary circulant graph of order n doesn’t exist when n has any prime factor of the form 2(2m ⁻ 1)+1, m ^∈ _N.

Proof. Using Theorem 2.3, n = 4a+1, a+1 ∈ _N. Let n = p₁ⁿ¹p₂ⁿ² …p_j^nj where p₁,p₂,…,p_j are the (odd) prime factors of n. Let p_i , 4m + 1 for at least one i, 1 ≤ i ≤ j and for any m ∈ _N. This implies, p_i = 2(2q − 1) + 1 for some q ∈ _N. Consider the circulant graph C. Let r be the natural number such that r = _pⁿi .

Aim To find out all natural numbers lying between 1 and n such that g.c.d. of each one of them with n is exactly r.

Let gcd(n,pr + s) = r where p,s + 1 ∈ _N such that 0 ≤ s < r and 1 ≤ pr + s ≤ n = rp_i. This implies that s = 0 and so gcd(n,rp+s) = gcd(n,rp) = gcd(rp_i,rp) = r where 1 ≤ pr ≤ p_ir = n. Thus we get gcd(p,p_i) = 1 where p ≤ p_i which is greater than 1. Therefore the possible values of p are 1,2,…,p_i − 1.

Thus r,2r,3r,…,(p_i − 1)r are the only numbers lying between 1 and n such that g.c.d. of n with each one of them is exactly r. This implies r,2r,3r,…,(p_i − 1)r are the possible periods of cycles of length p_i each, in C_n(1,2,…,^hn₂ⁱ) since the length of a cycle of period rp

in Cn(1,2,…,hn2i) is gcd(nn,rp) = gcd(rprpii,rp) = gcdp(pii,p) = pi for p = 1,2,…,p_i − 1, using Theorem 1.2.

In C_n(1,2,…,^hn₂ⁱ),

the cycles of period r and n − r(= (p_i − 1)r) are the

same, the cycles of period 2r and (p_i − 2)r are the same,

… the cycles of period (pi−21)r and (pi+1)2 r are the same. Thus, there are pi2−1 number of possible distinct periodic cycles of (periods r,2r,…, ^pi₂⁻¹ and) length p_i, each in C_n(1,2,…,^hn₂ⁱ).

Now, ^pi₂⁻¹ = 2q − 1 is an odd number. This implies, any circulant graph of order n and its complementary circulant graph contain unequal number of periodic cycles of length p_i, each. This implies that self-complementary circulant graph of order n does n’t exist when n contains any prime factor of the form 2(2q − 1)+1, q ∈ _N, by Remark 2.5.

Thus, when n = 9,21,33,49,57,69,77,81,93, etc., self-complementary circulant graph doesn’t exist on n vertices, by Theorem 2.6, even though in each case, n ≡ 1 (mod 4).

Now, by combining Theorem 2.6 and the sufficient condition for the existence of a self-complementary circulant graph of order n, we get the following result.

Theorem 2.7. [17] The necessary and sufficient condition for the existence of a self-complementary circulant graph of order n is that each prime factor p of n should satisfy p ≡ 1(mod 4).

3. On Isomorphism of Circulant Graphs

In this section, Type-2 isomorphism, a new type of isomorphism different from already known Adam’s isomorphism of circulant graphs, main results related to it and families of new abelian groups obtained from isomorphic circulant graphs are presented. Type-2 isomorphic circulant graphs have the property that they are isomorphic graphs without Cayley Isomorphism (CI) property.

Definition 3.1. [12] A circulant graph C_n(R) is said to have the CI-property if whenever C_n(S) is isomorphic to C_n(R), there is some a ∈ _Z^∗_n for which S = aR.

Lemma 3.2. [16] Let S be a non-empty subset of Z_n and x ^∈ Zn. Define a mapping Φn,x : S ^→ Zn such that Φ_n,x(s) = xs for every s ∈ S under multiplication modulo n. Then, Φ_n,x is bijective if and only if S = Z_n and gcd(n,x) = 1.

Definition 3.3. [16]                        Circulant graphs C_n(R) and

C_n(S) for R = {r₁,r₂, …,r_k} and S = {s₁,s₂,…,s_k} are Adam’s isomorphic if there exists a positive integer x relatively prime to n with S = {xr₁, xr₂, …, xr_k}^∗_n where

, the reflexive modular reduction of a sequence < r_i > is the sequence obtained by reducing each r_i modulo n to yield r_i⁰ and then replacing all resulting termsⁿ by n − r_i0. r_i⁰ which are larger than ₂

Lemma 3.4. [16] Let m,r,t ∈ _Zn ∈ gcd(n,r) = m > 1 and . Then the mapping ^Θ_n,r,t : Z_n ^→ Zn defined by Θ_n,r,t(x) = x+jtm for every x ∈ Z_n under arithmetic modulo n is bijective where x = j+qm, 0 ≤ j ≤ m−1,  and j,q ^{∈ Z}n.

Theorem 3.5. [16] Let V (C_n(R)) = {v₀,v₁,…,v_n−₁}, V (K_n) = {u₀, u₁,…,u_n−₁} and r ∈ R ∈ gcd(n,r) = m > 1. Then the mapping Θ_n,r,t : V (C_n(R)) → V (K_n) defined by Θ_n,r,t(v_x) = u_x+jtm and Θ_n,r,t((v_x, v_x+s)) = (Θ_n,r,t(v_x),Θ_n,r,t(v_x+s)) for every x ^∈ Zn, x = j + qm,  and s ∈ R, under sub-

script arithmetic modulo n, for a set R = {r₁, r₂, …, r_k, n − r_k, n − r_k−₁, …, n − r₁} is one-to-one, preserves adjacency and Θ_n,r,t(C_n(R))  C_n(R) for t = 0,1,2,…, _mⁿ − 1.

Definition 3.6. [16] For a given C_n(R) and for a particular value of t,

for some S and S , xR for all x ∈ Φ_n under reflexive modulo n, then C_n(R) and C_n(S) are called Type-2 isomorphic circulant graphs w.r.t. r, r ∈ R. In this case, subsets R and S of Z_n are called Type-2 isomorphic subsets of Zn w.r.t. r.

Clearly, Type-2 isomorphic circulant graphs are circulant graphs without CI-property. We obtained the following results on Type-2 isomorphism.

Theorem 3.7. [16] For n ≥ 2, k ≥ 3, 1 ≤ 2s−1 ≤ 2n−1, n , 2s−1, R = {2s−1,4n−2s+1,2p₁,2p₂,…,2p_k−₂} and S = {2n − (2s − 1), 2n + 2s − 1,2p₁,2p₂,…,2p_k−₂}, circulant graphs C_8n(R) and C_8n(S) are Type-2 isomorphic (and without CI − property) where gcd(p₁,p₂,…,p_k−₂) = 1 and n,s,p₁,p₂,…,p_k−₂ ^∈ N.

Theorem        3.8.     [16]     For      R      =      {2r         − 1,2s −

1,2p₁,2p₂,…,2p_k−₂^}, n ^≥ 2, k ,

,…,p_k−₂) = 1 and

n,r,s,t,p₁,p₂,…,p_k−₂ ^∈ N, if Θ_n,2,t(C_n(R)) and C_n(R) are Type-2 isomorphic circulant graphs for some t, then n ≡ 0 (mod 8), 2r − 1+2s − 1 = ⁿ, t = ⁿ or ³ⁿ, 2r − 1 , ⁿ, ≥ 16.

Definition 3.9. [1]                               Let Ad_n = {Φn,x : x ∈ Φ_n},

Ad_n(R) = ^{Φn,x(R) : x ^∈ Φ_n^} = ^{xR : x ^∈ Φ_n^} and Ad_n(C_n(R)) = T 1_n(C_n(R)) = {Φn,x(C_n(R)) : x ∈ Φ_n} = ^{C_n(xR) : x ^∈ Φ_n^} for a set R = ^{r₁,r₂,…,r_k, n ⁻ r_k, n ⁻ r_k−1,…,n ⁻ r₁^{} ⊆} Zn. Define ^0◦0 in Ad_n(C_n(R)) such that Φn,x(C_n(R)) ◦ Φn,y(C_n(R)) = Φn,xy(C_n(R)) and C_n(xR) ◦ C_n(yR) = C_n((xy)R) for every x,y ∈ Φ_n, under arithmetic modulo n. Clearly, Ad_n(C_n(R)) is the set of all circulant graphs that are Adam’s isomorphic to C_n(R) and (Ad_n(C_n(R)),◦) = (T 1_n(C_n(R)), ◦) is an abelian group and we call it as the Adam’s group or Type-1 group on C_n(R) under ^0◦0.

Definition 3.10. [1] Let V (C_n(R)) = {v₀,v₁,…,v_n−₁}, V (K_n) = ^{u₀, u₁, …, u_n−₁^}, r ^∈ R, m,q,t,t⁰,x ^∈ Zn such that gcd(n,r) = m > 1, x = j + qm, 0 ≤ j ≤ m ⁻ 1 and 0 ^≤ q,t,t. Define Θ_n,r,t : Z_n ^→

Zn and Θ_n,r,t : V (C_n(R)) ^→ V (K_n) such that Θ_n,r,t(x) = x + jtm, Θ_n,r,t(v_x) = u_x+jtm and Θ_n,r,t((v_x,v_x+s)) = (Θ_n,r,t(v_x),Θ_n,r,t(v_x+s)) for every x ^∈ Zn and s ^∈ R, under subscript arithmetic modulo n. Let s ∈ Z_n, V_n,r = {Θ_n,r,t : t = 0,1,…, , V_n,r(s) = {Θ_n,r,t(s) : t = 0,1,…, and V_n,r(C_n(R)) = {Θ_n,r,t(C_n(R)) : t = 0,1,…, . Define 0◦0 in Vn,r such that (Θn,r,t ◦ Θn,r,t0 ) = Θn,r,t+t0 , (Θn,r,t ◦ Θn,r,t0 )(x) (= Θn,r,t(Θn,r,t0 (x)) = Θn,r,t(x + jt0m) = (x + jt⁰m) + jtm = x + j(t + t⁰)m) = Θ_n,r,t+t⁰ (x) and

Θn,r,t(Cn(R)) ◦ Θn,r,t0 (Cn(R)) = Θn,r,t+t0 (Cn(R)) for every Θ_n,r,t,Θ_n,r,t⁰ ∈ V_n,r where t + t⁰ is calculated under addition modulo . Clearly, (V_n,r(s), ◦) and (V_n,r(C_n(R)), ◦) are abelian groups for every s ∈ _Zn.

V_n,r(C_n(R)) contains all isomorphic circulant graphs of Type-2 of C_n(R) w.r.t. r, if exist. Let T 2_n,r(C_n(R)) = {C_n(R)} ∪ {C_n(S) : C_n(S) is Type-2 isomorphic to C_n(R) w.r.t. r}. Thus, T 2_n,r(C_n(R)) = {C_n(R)} ∪ {Θ_n,r,t( C_n(R)) : Θ_n,r,t(C_n(R)) = C_n(S) and C_n(S) is Type-2 isomorphic to C_n(R) w.r.t. r, 0 ≤ t ≤ mn − 1} = {Θn,r,0(Cn(R))} ∪ {Θn,r,t(Cn(R)) : Θn,r,t(Cn(R))

= C_n(S) and C_n(S) is Type-2 isomorphic to C_n(R),  V_n,r(C_n(R)) and (T 2_n,r(C_n(R)), ◦) is a subgroup of (V_n,r(C_n(R)), ◦). Clearly, T 1_n(C_n(R)) ∩ T 2_n,r(C_n(R)) = {C_n(R)}. And C_n(R) has Type-2 isomorphic circulant graph w.r.t. r if and only if T 2_n,r(C_n(R)) , {C_n(R)} if and only if T 2_n,r(C_n(R)) ∩ {C_n(R)} ,Φ if and only if |T 2_n,r(C_n(R))| > 1 [1].

Definition 3.11. [1] For any circulant graph C_n(R), if T 2_n,r(C_n(R)) , {C_n(R)}, then (T 2_n,r(C_n(R)), ◦) is called the Type-2 group of C_n(R) w.r.t. r under ‘ ◦⁰ .

Theorem 3.12. [1] Let p be an odd prime and k ≥ 3. Then, for i = 1 to p, d_i = (i − 1)np + 1 and R_i = {d_i, np^{2 −} d_i,np² + d_i,2np^{2 −} d_i,2np² + d_i,3np^{2 −} d_i, 3np² + d_i,…,(p−1)np²−d_i,(p−1)np²+d_i,np³−d_i,pp₁,pp₂,…, pp_k−2, p(np^{3 −} p_k−2), p(np^{3 −} p_k−3), …, p(np^{3 −} p₁)^}, circulant graphs C_np3(R_i) are Type-2 isomorphic (and without CI-property) where gcd(p₁,p₂,…,p_k−₂) = 1 and n,p₁,p₂,…,p_k−₂ ^{∈ N}.

Theorem 3.13. [1] Let p be an odd prime, k ≥ 3, 1 ≤ i ≤ p, d_i = (i − 1)np + 1, R_i = {d_i, np² − d_i, np² + d_i, 2np² − d_i, 2np² + d_i, 3np² − d_i, 3np² + d_i, …, (p − 1)np² − d_i, (p − 1)np² + d_i, np³ − d_i, pp₁, pp₂, …, pp_k−2, p(np^{3 −} p_k−2), p(np^{3 −} p_k−3), …, p(np^{3 −} p₁)^},

T 2(R_i) = ^{Θ_np3,p,jn(R_i) : j = 1,2,…,p^}, T 2(C_np3(R_i)) = ^{Θ_np3,p,jn(C_np3(R_i)) : j = 1,2,…,p^}, gcd(p₁,p₂,…,p_k−2)

= 1 and n,p₁,p₂,…,p_k−₂                                            ^∈ N. Then T ²_np3,p(R_i)

=      T 2(R_j),        T 2_np3,p(C_np3(R_i))       =      T 2(C_np3(R_j))      and

(V_np3,p(R_i), ◦), (V_np3,p(C_np3 (R_i)), ◦) and (T ²_np3,p(R_i), ◦) are abelian groups, 1 ≤ i,j ≤ p. Moreover, (T 2_np3_,p(C_np3( R_i)), ◦) is the Type-2 group of order p on C_np3(R_i) w.r.t. r = p, 1 ^≤ i,j ^≤ p.

Circulant graphs C₁₆(1,2,7) and C₁₆(2,3,5) are Type-2 isomorphic and C₂₇(1,3,8,10), C₂₇(3,4,5,13) and C₂₇(2,3,7,11) are also. See Figures 1–5.

4. CartesianProductandFactorization of Circulant Graphs

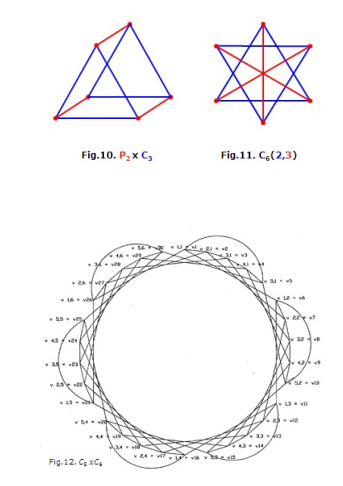
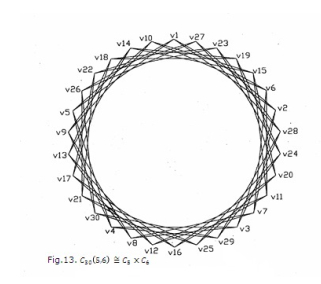
Just as integers can be factored into prime numbers, there are many results on decompositions of structures throughout mathematics [6]. The standard products – Cartesian, lexicographic, tensor, and strong – all belong to a class of products introduced by Imrich and Izbicki and called B − products [8]. In this section, a few important results that are obtained in our study of Cartesian product and factorization of circulant graphs, similar to the theory of product and factorization of natural numbers, are presented [15]. Graphs C₅C₆ and C₃₀(5,6) are isomorphic and are given in Figures 12 and 13. One can see the difficulty of this study from this example.

Definition 4.1. [9] The cross product or Cartesian product of two simple graphs G(V ,E) and H(W,F) is the simple graph G  H with vertex set V × W in which two vertices u = (u₁,u₂) and v = (v₁,v₂) are adjacent if and only if either u₁ = v₁ and u₂v₂ ∈ F or u₂ = v₂ and u1v1 ∈ E.

Theorem 4.2. [15] Let G be a connected graph of order n, n > 2. Then, P₂  G is circulant if and only if G  H or P₂  H where H is a connected circulant graph of odd order.

Theorem 4.3. [15] Let G be a connected graph of order n ≥ 2. Then C₄G is circulant if and only if G is circulant of odd order.

Theorem 4.4. [15] If G and H are connected graphs and G  H is circulant, then G and H are circulants.  Graphs P₂C₃ and P₂C₄ are given in Figures 10 and 11 and C₅C₆ and C₃₀(5,6)  C₅C₆ in 12 and 13, respectively.

Theorem 4.5. [15] Let G and H be connected graphs, each of order > 2. Then G  H is circulant if and only if G and H are circulants and satisfy one of the following conditions:

• G C_m(R); H  C_n(S) and gcd(m,n) = 1.
• G C₂m+1(R); H  C₂n+1(S), P₂  C₂n+1(S), C₄  C₂n₊₁(S) or C₂k₍₂n₊₁₎(S) and gcd(2m+1,2^k(2n+1))

= 1, k ^{∈ N}.

• G P); H  C_2n+1(S) or P₂  C_2n+1(S) and gcd(2m+1,2n+1) = 1.
• G ^C₂k(2m+1)(R) , P₂  ^C₂k−1(2m+1)(T ) for any

C₂k−₁(2m+1)(T ); H  C₂n+1(S) and gcd(2^k(2m + 1),2n+1) = 1, k ∈ _N.

 C_2m+1(R); H  C_2n+1(S) and gcd(2m + 1,2n+1) = 1.

(vi) G  ^C₂^k(2m+1)(R) , C₄  ^C₂^k−2(2m+1(T ), P₂

 ^C₂k−1(2m+1)(U) for any ^C₂k−2(2m+1(T ) and C₂k−₁(2m+1)(U); H  C₂n+1(S) and gcd(2^k(2m + 1),2n+1) = 1, k ∈ _N, k ≥ 2.

Definition 4.6. [15] A non-trivial graph G is said to be prime if G  implies G₁ or G₂ is trivial; G is composite if it is not prime.

Definition 4.7. [15] If C_m(R), C_n(S) and C_mn(T ) are circulant graphs such that C_m(R)  C_n(S)  C_mn(T ), then we say that C_m(R) and C_n(S) are divisors or factors of C_mn(T ).

Thus for any connected circulant graph, the graph and C₁( ) = K₁ are always divisors and so we call them as improper divisors of the circulant graph. Divisors which are integer multiple of improper divisors also be called as improper divisors of the circulant graph. This doesn’t arise since we consider divisors of connected graphs only. Divisor(s) other than improper divisors is called proper divisor(s) of the circulant graph.

Definition 4.8. [15] A circulant graph whose only divisors are improper is called a prime circulant graph. Other circulant graphs are called composite circulant graphs.

Theorem 4.9 (Factorization Theorem On Circulant

Graphs). [15]

Let m and n be relatively prime integers. If R, S  and T  with T = dnR ∪ dmS for some d such that gcd(mn,d) = 1, then C_mn(T )  C_m(R)  C_n(S).

Theorem 4.10. [15] If n , 4 and 1 ∈ R, then C_n(R) is a prime circulant.

Corollary 4.11. [15] If n , 4 and R contains an integer relatively prime to n, then C_n(R) is prime circulant.

Corollary 4.12. [15] If n is a prime power other than 4 and C_n(R) is connected, then C_n(R) is prime circulant for all R , φ.

Theorem 4.13 (Fundamental Theorem of Circulant Graphs). [15]

Every connected circulant graph is the unique product of prime circulant graphs (uniqueness up to isomorphism).

Remark 4.14. [15]           If G is a connected graph such that

G  G₁  G₂  …  G_k, then the diameter of G, dia(G) = ^Pk_i=1dia(G_i) [10].

Thus, we can find the diameter of any given circulant graph, provided diameters of its prime circulant graphs are known. Also the above relation helps to generate (circulant) graphs of bigger diameters.

Remark 4.15. [15]

1. In prime factorization of connected circulants C₁( ) = K₁ and C₂ = P₂ act similar to 1 and 2 among the set of all natural numbers, respectively. Thus, C₁( ) is a unit, like 1 in number theory.
2. There exist two types of prime circulant graphs of order n, one with periodic cycle(s) of length n and the other without periodic cycle of length n.
3. The theory of factorization of circulants is similar to the theory of factorization of natural numbers and one of the very few well-known mathematical structures so vividly classified (expressed) in terms of prime factors. It can be applied in cryptography.
4. exe is a VB program developed by us to show visually how the transformation Φ_m,n acts on C_m C_n for different values of m and n, m,n ∈ _N.
5. An interesting problem is, for a given integer n, finding the number of prime (composite) circulant graphs of order either equal to n or less than or equal to n.
6. One can develop theories similar to the theory of Cartesian product and factorization of circulant graphs to the other standard products of circulant graphs.

Conclusion

This study covers a few isomorphic properties of circulant graphs. One can go for a similar study on Cayley graphs.

Acknowledgment

The author expresses his sincere thanks to Prof. Lowell W Beineke, Indiana-Purdue University, U.S.A., Prof. Brian Alspach, University of Newcastle, Australia, Prof. M.I. Jinnah, University of Kerala, Trivandrum, India and Prof. V. Mohan, Thiyagarayar College of Engineering, Madurai, Tamil Nadu, India for their valuable suggestions and guidance and Dr. A. Christopher, Dr. P. Wilson and Mr. R. Satheesh of S.T. Hindu College, Nagercoil, India for their assistance to develop the VB programs to show how the transformations defined on circulant graphs to obtain their isomorphic graphs is taking place. He also expresses his gratitude to Central University of Kerala (CU Kerala), Periye – 671 316, Kasaragod, Kerala, India and St. Jude’s College, Thoothoor – 629 176, Kanyakumari District, Tamil Nadu, India for providing facilities and CU Kerala and Lerroy Wilson Foundation, India (www.WillFoundation.co.in) for providing financial assistance to do this research work.

1. Vilfred, “A few properties of circulant graphs: Selfcomplementary, isomorphism, Cartesian product and factorization” in 7th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO2017), American University of Sharjah, Sharjah, April 2017.
2. J. Davis, Circulant Matrices, Wiley, New York, 1979.
3. Adam, “Research problem 2-10”, J. Combinatorial Theory, 3, 393, 1967.
4. Alspach, J. Morris and V. Vilfred, “Self-complementary circulant graphs”, Ars Com., 53, 187–191, 1999.
5. Alspach and T. B. Parsons, “Isomorphism of circulant graphs and digraphs”, Discrete Math., 25, 97–108, 1979.
6. Arratia, A. D. Barbour and Simon Tavare, “Random Combinatorial Structures and Prime Factorizations”, A.M.S.Notices, 44, 903–910, 1997.
7. T. Boesch and R. Tindell, “Circulant and their connectivities”, J. Graph Theory, 8, 487–499, 1984.
8. Elspas and J. Turner, “Graphs with circulant adjacency matrices”, J. Combinatorial Theory, 9, 297–307, 1970.
9. Harary, Graph Theory, Addison-Wesley, Reading, M.A., 1969.
10. Imrich and H. Izbicki, “Associative products of graphs”, Monatsh. Math., 80, 277–281, 1975.
11. Kra and S. Simanca, “On Circulant Matrices”, AMS Notices, 59 (3), 368–377, 2012.
12. H. Li, “On isomorphisms of finite Cayley graphs-a survey”, Discrete Math. 256, 301–334, 2002.
13. Sabidussi, “Graph multiplication”, Math. Z., 72, 446– 457, 1960.
14. Sachs, “Uber selbstkomplementare Graphen”, Publ. Math. Debrecen, 9, 270–288, 1962.
15. Vilfred, “A Theory of Cartesian Product and Factorization of Circulant Graphs”, Hindawi Pub. Corp. – J. Discrete Math., Vol. 2013, Article ID 163740, 10 pages.
16. Vilfred, “New Abelian Groups from Isomorphism of Circulant Graphs”, Proce. of Inter. Conf. on Applied Math. And Theoretical Computer Science, St.Xaviers Catholic Engineering College, Nagercoil, Tamil Nadu, India, xiii–xvi, 2013.
17. Vilfred, “ P -labelled Graphs and Circulant Graphs”, Ph.D. Thesis, University of Kerala, Trivandrum, India, 1994.
18. Vilfred and P. Wilson, “New Families of Circulant graphs without Cayley Isomorphism Property with mi = 5”, Int. Journal of Scientific and Innovative Mathematical Research, 3 (6), 39–47, 2015.
19. Vilfred and P. Wilson, “New Family of Circulant Graphs without Cayley Isomorphism Property with mi = 7”, IOSR Journal of Mathematics, 12, 32–37, 2016.
20. Zhang, “Self-complementary symmetric graphs”, J. Graph Theory, 16, 1–5, 1992.

(Click to view)

(Click to view)