1. Introduction

This paper is an extension of work originally presented in 4th International Conference on Electrical and Electronics Engineering [1]. The purpose of this work is solving economic load dispatch problem with a lot of constraints through with new optimization technique Vortex Search Algorithm.

  Economic load dispatch of a power system is very important in terms of control and planning of that power system. Main goal of ELD is distributed total demand power among the committed thermal generation units with minimum production cost by satisfying set of equality and inequality constraints. If ELD problem is not solved for thermal power plants, demand power may be generated very costly. ELD problem can be basically modeled second order (quadratic) function [2].  However, this function may became more complex, non-smooth and non-convex with some constraints such as valve point loading effect, ramp rate limits, transmission line losses and prohibited zones.

Economic load dispatch plays very big role for operated power plants. For this reason, a lot of researcher studied this issue. A number of optimization techniques developed and applied to ELD problem. Quadratic Programming [3], Linear Programming [4], Non-Linear Programming [5], Lambda Iteration Method [6] etc. techniques were used for solving ELD problem. These traditionally techniques gives good results for basic ELD problem but these techniques may poor results when constraints and complexity are increased.

Together with the advances in the computer sciences, a lot of random search optimization techniques developed and used [7]. Different Evolution [8], Particle Swarm Optimization [9], Genetic Algorithm [10], Artificial Bee Colony [11], Harmony Search [12], Bacterial Foraging Optimization [13], Firefly Algorithm [14], Ant Colony Optimization [15] etc. are some of these techniques. User defined parameters are necessary for these optimization techniques. If the parameters are not chosen properly, the results obtained from these techniques may not be good results.

The organization of this paper as follows: Economic load dispatch, main objective of ELD, constraints of ELD and mathematical express of ELD are described in Section 2. Vortex Search Algorithm and its mathematical model are described in Section 3. Using test system, its parameters, obtained results and figures are described in Section 4. Finally evaluation of this paper is briefed in Section 5.

2. Economic Load Dispatch

There are a lot of operating cost for thermal power plants such as fuel cost, personal fees etc.. In these costs the biggest share is fuel cost of thermal generation units. For this reason solving economic load dispatch problem for thermal power plants is necessity. Main objective of economic load dispatch is keep the total fuel cost as minimum level while meet the total demand power. Basically defined cost function of ELD as a quadratic function as follows:

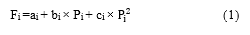2.1.  Valve Point Loading Effect

Due to opening stream valves at the power systems losses are increased. This effect is called valve point loading effect. Due to system losses are increased wit valve point loading effect, total cost value is increased. Above equation has sinusoidal terms due to valve point loading effect. This situation can be seen in Figure 1. This transformed equation is expressed as follows:

            F_i = a_i + b_i × P_i + c_i ×  + |e_i × sin(f_i × (  – P_i))       (2)

F_i represents resulting fuel cost value, P_i represent power of thermal generator, a_i, b_i, c_i are cost coefficients and e_i, f_i are valve point loading coefficients of thermal generator unit i.

Total cost value of system is obtained by summed cost values of every thermal generation units.

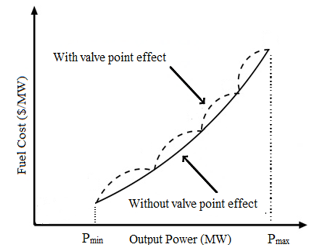Figure 1 With and without valve point effect

2.2.  Generators Limits

Thermal generators units must operate maximum and minimum power range. This power range can be different for different units:

                                         P_i,max ≥ P_i ≥ P_i,min                                    (3)

Pi,min and Pi,max are represent minimum generator limit and maximum generator limit of unit i.

2.3.  Power Balance

Total generated power at the thermal power plants meet the demand power by consumers. For this reason transmission line losses must be considered.  The total generated power obtained sum of total demand power and total transmission line losses.

Transmission line losses is calculated as follows:

                  P_loss = P_iB_ijP_j + B_0iP_i + B₀₀             (4)

Total generated power is calculated as follows:

                                       P_i = P_d + P_loss                                  (5)

N represent total thermal power plant. Pd and Ploss represent total demand power by consumer and total transmission line losses respectively. Bij, B0i and B00 are transmission loss coefficients.

2.4.  Ramp Rate Limits

While a thermal generator unit is operating at a certain point, the operating point can only be increased to a certain level determined by the up ramp rate limit or decreased to a certain level determined by the down ramp rate limit.

This situation is shown as follows:

URi represents the up-ramp rate limit, DRi represent down ramp rate limit,   is previous generated power and Pi present generated power of unit i.

2.5.  Prohibited Zone

In some cases, thermal generation units do not worked and do not want to be worked some reasons such as mechanical corruption some particular power range (prohibited zone). These conditions can be expressed as follows:

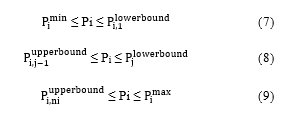j represents number of prohibited zones of unit i and j=2, 3, 4 …ni.   represents lower limit and  represents  upper limit of jth prohibited zone. Prohibited zone effect is shown in Figure 2.

3. Vortex Search Algorithm

Vortex search algorithm is a new optimization technique and inspired by stirring liquid materials.[17,18]. VSA is very influential and handy technique for solving economic load dispatch problem.  problem. As a result of using an extensible step size modification arrangement a good balancing explorative and exploitative behavior of the search are obtained [18]. Vortex patterns can be represented in two dimensional space as a lot of nested circuits. The biggest and outer circuit is starting circuit of search space. The center of this circuit is calculated as follows:

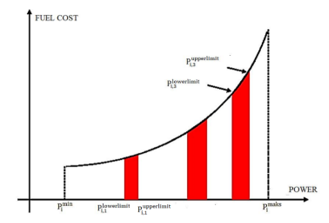Figure 2 Shown of prohibited zones [16]

Upperlimit and lowerlimit are maximum and minimum constraints of the problem. A lot of candidate solutions are constituted into the outer circuit. The initial standard deviation is accepted as radius of this outer circuit and calculated as follows:

                          µ₀ = (upperlimit + lowerlimit) / 2                   (10)

               σ₀ = (max (upperlimit) – min (lowerlimit)) / 2        (11)

Generated candidate solutions must be controlled for ensure these solutions within the maximum and minimum limits of the problem. If these candidate solutions are not into the search space, they must be shifted into the search space. Some candidate solutions, which are not into the search space, shifted into the search space using equation as follows:

             = lowerlimitⁱ + (upperlimitⁱ –lowerlimitⁱ)×rand    (12)

After this step a candidate solution, which is the best solution into the search space, is selected. This best solution is represented s’.  This solution is memorized and current center μ0 is shifted to s’. New candidate solutions are constituted around this new center. All of candidate solutions are compared with previous best solution. If there is a better solution than s’, it is selected as a new best solution [19]. This situation continues each iteration step. Radius of the circuits must be decreased every iteration. For this reason inverse gamma function (gammaincinv) is used and new radius is calculated every iteration as follows:

                       rt = σ0 × (1 / x) × gammaincinv(x, a_t)               (13)

a_t is changeable parameter and it dependent a₀, t and MaxItr. This function shown as follows:

a_t = a₀ – (t / MaxItr)                 (14)

Where t represents iteration number,  MaxItr  represents  maximum iteration number. Due to cover the all search space a₀ is chosen 1. Outline flowchart of VSA method is shown in Figure 3:

4. Test System and Results

Vortex search algorithm was proposed and used for solving economic load dispatch problem. Six generation unit power system was selected. VSA algorithm was applied to this system considering various constraints. Each cases the number of iteration is limited to 1000 for obtained good solutions.

Case1 constraints are ramp rate limits and transmission losses;

Case2 constraints are ramp rate limits, prohibited zones and transmission losses;

Case3 constraints are transmission losses, valve point loading effect and ramp rate limits;

For every case transmission line losses coefficients are same and given as follows:

B=10^-4 ×

0.17	0.12	0.07	-0.01	-0.05	-0.02
0.12	0.14	0.09	0.01	-0.06	-0.01
0.07	0.09	0.31	0.01	-0.10	-0.06
-0.01	0.01	0.00	0.24	-0.06	-0.08
-0.05	-0.06	-0.10	-0.06	1.29	-0.02
-0.02	-0.01	-0.06	-0.08	-0.02	1.5

B₀=10^-4 ×

-3.9080

-1.2970

7.0470

0.5910

2.1610

-6.6350

B₀₀=0.056

4.1.  Case 1: ELD with Ramp Rate

For this case two different constraints, which are ramp rate limits and transmission line losses, applied to system. Cost coefficients, ramp rate limits data and maximum – minimum limits of generators are shown in Table 1. Results of VSA was given Table 2 with different optimization techniques. Convergence behavior of VSA for this case was shown Figure 4. For this case selected power is 1263MW.

Table 1 Data of Case 1

Unit	a	b	c	P0	UR	DR	Pmin	Pmax
1	240	7	0.0070	440	80	120	100	500
2	200	10	0.0095	170	50	90	50	200
3	220	8.5	0.0090	200	65	100	80	300
4	200	11	0.0090	150	50	90	50	150
5	220	10.5	0.0080	190	50	90	50	200
6	190	12	0.0075	150	50	90	50	120

Table 2 Results for Case 1

P(MW)	VSA	PSO	CPSO	WIPSO
P1	457.0630	493.24	471.66	454.39
P2	172.3751	114.63	140.03	164.279
P3	264.3900	263.41	240.06	264.223
P4	141.4373	139.71	149.97	123.21
P5	164.0545	179.65	173.78	167.22
P6	76.1690	84.83	99.97	120.00
Ploss	12.4889	12.22	12.38	12.24
Cost($)	15448	15489	15481.87	15453.13

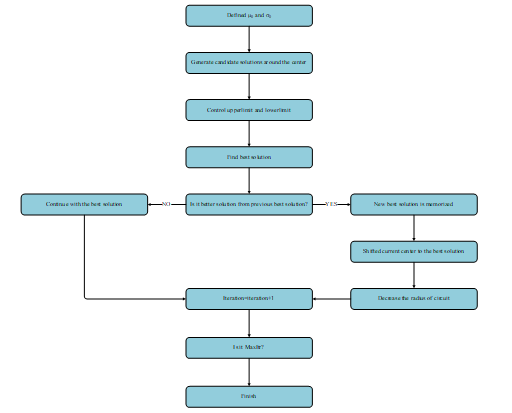Figure 3 Outline flowchart of VSA

Results of vortex search algorithm compared with PSO, CPSO and WIPSO techniques from [20]. It is clear that from the Table 2 proposed VSA method has capable of the finding best solutions and minimum cost value. Figure 4 is shown convergence behavior of VSA for this case.

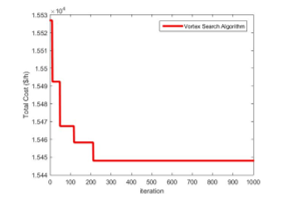Figure 4 Convergence behavior of VSA for Case1

4.2.  Case 2: ELD with Prohibited Zone

For this case three different constraints, which are ramp rate limits, prohibited zones and transmission line losses, applied to system. Cost coefficients was given in Table 3. Prohibited zone ranges and maximum – minimum limits of generators were given in Table 4. Ramp rate limits was given in Table 5. Convergence behavior of VSA for this case was shown Figure 5. 1263 MW power was selected for demand power.  Results of VSA and other techniques results are shown in Table 6.

Table 3 Cost Coefficients

Unit	a	b	c
1	240	7	0.0070
2	200	10	0.0095
3	220	8.5	0.0090
4	200	11	0.0090
5	220	10.5	0.0080
6	190	12	0.0075

Table 4 Limits and Prohibited Zones of Generators

Unit	Pmax	Pmin	Prohibited Zone
1	500	100	210-240, 350-380
2	200	50	90-110, 140-160
3	300	80	150-170, 210-240
4	150	50	80-90, 110-120
5	200	50	90-110, 140-150
6	120	50	75-85, 100-105

Table 5 Ramp Rate Limits

Unit	P0	UR	DR
1	440	80	120
2	170	50	90
3	200	65	100
4	150	50	90
5	190	50	90
6	150	50	90

Table 6 Results for Case 2

P(MW)	VSA	MFO	PSO	GA
P1	446.03	426.08	447.49	474.80
P2	181.09	199.80	173.32	178.63
P3	263.45	247.49	263.47	262.20
P4	133.96	136.94	139.05	134.28
P5	176.65	166.24	165.47	151.90
P6	74.53	98.93	87.12	74.18
Ploss	12.73	12.51	12.95	13.02
Cost($)	15447	15448.7	15450	15459

According to given results from Table 6, proposed VSA method has better cost value when compared with the MFO, PSO, GA techniques from [21].

Figure 5 is shown convergence behavior of VSA for this case.

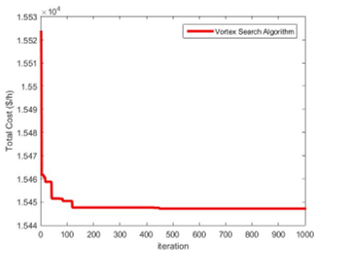Figure 5 Convergence behavior of VSA for Case 2

4.3.  Case 3: ELD with Valve Point Loading Effect

For this case three different constraints, which are transmission line losses, valve point loading effect and ramp rate limits, applied to system. Cost coefficients and valve point loading effect coefficients are given in Table 7. Obtained results were given in Table8 and compared with different methods. Convergence behavior of VSA for this case was shown Figure 6. 1263 MW power was selected for demand power.

Results of VSA and other techniques results was shown in Table 8. Maximum and minimum limits of generators are same with Table 4 and ramp rate limits are same with Table 5. Demand power is selected 1263 MW for this case.

Table 7 Valve point effect and cost coefficients

Unit	a	b	c	e	f
1	240	7	0.0070	300	0.031
2	200	10	0.0095	150	0.063
3	220	8.5	0.0090	200	0.042
4	200	11	0.0090	100	0.08
5	220	10.5	0.0080	150	0.063
6	190	12	0.0075	100	0.084

Table 8 Results for Case 3

P(MW)	VSA	PSO	CPSO	WIPSO	MRPSO
P1	495.29	443.03	467.55	437.82	442.07
P2	195.90	169.03	163.05	173.28	167.23
P3	235.79	262.02	253.41	271.97	267.09
P4	65.62	134.78	115.07	138.70	132.81
P5	197.82	147.47	169.45	146.98	155.02
P6	87.27	125.35	113.24	103.63	107.02
Ploss	12.92	18.68	18.70	18.08	18.03
Cost($)	15746	16372.9	16329.2	16327	16310.76

It is obviously seen that from the Table 8 VSA, method gave best cost value when compared with   from PSO, CPSO, WIPSO and MRPSO techniques from [22].

Figure 6 is shown convergence behavior of VSA for this case

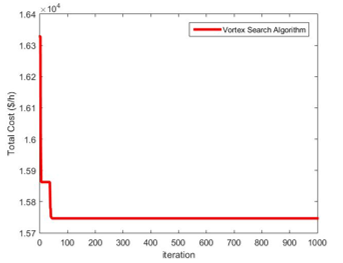Figure 6 Convergence behavior of VSA for Case 3

5. Conclusion

In this paper vortex search algorithm was applied to six generator power system for solving economic load dispatch problem. ELD problem was became more complex and more difficult problem with valve point loading effect, ramp rate limits, transmission line losses and prohibited zones constraints. Three different situation were analyzed and for first case minimum cost value was found 15448 $, for second case minimum cost value was found 15447 $, for third case minimum cost value was found 15746 $. Obtained results from VSA compared with another techniques from the literature. These results clearly show that VSA is very capable, feasible and effective method for solving non smooth and very complex economic load dispatch problem.

1. Saka, I. EKE, S. S. Tezcan, M. C. Taplamacioglu., “Economic Load Dispatch Using Vortex Search Algorithm” in 4^th International Conference on Electrical and Electronics Engineering, Ankara Turkey, 2017.
2. Sen. H. D. Mathur, “A New Approach to Solve Economic Dispatch Problem Using A Hybrid ACO–ABC–HS Optimization Algorithm”, Electrical Power and Energy Systems, 78, 735-744, 2016.
3. S. Coelho, V. C. Mariani, “Combining of Chaotic Differential Evolution and Quadratic Programming for Economic Dispatch Optimization with Valve-Point Effect”. IEEE Trans. Power Syst., 21, 989-996, 2006.
4. Farag, S. Al-Baiyat, T. C. Cheng, “Economic Load Dispatch Multi Objective Optimization Procedures Using Linear Programming Techniques” IEEE Trans. Power Syst., 10, 731-738, 1995.
5. Papageorgiou, E. Fraga, “A Mixed Integer Quadratic Programming Formulation for the Economic Dispatch of Generators with Prohibited Operating Zones” Electr. Power Syst. Res., 77, 1292-1296, 2007.
6. L. Chen, S. C. Wang, “Branch-and-Bound Scheduling for Thermal Generating Units”, IEEE Transactions on Energy Conversion, 8(2), 184–189, 1993.
7. Bhui, N. Senroy, “A Unified Method for Economic Dispatch with Valve Point Effects” in IEEE Int. Con. Power Systems, 1-5, 2016.
8. Balamurugan, S. Subramanian, “Differential Evolution-Based Dynamic Economic Dispatch of Generating Units with Valve-Point Effects,” Electric Power Components and Systems, 36, 828-843, 2008.
9. Sriyanyong, “An Enhanced Particle Swarm Optimization for Dynamic Economic Dispatch Problem Considering Valve-Point Loading,” in Proc. the Forth IASTED International Conference on Power and Energy Systems (AsiaPES 2008), 167-172, 2008.
10. L. Chiang, “Genetic-Based Algorithm for Power Economic Load Dispatch” IET Gener. Trans. Distrib., 1, 261-269, 2007.
11. Hemamalini, S. P. Simon, “Artificial Bee Colony Algorithm for Economic Load Dispatch Problem with Non-Smooth Cost Functions” Electr. Power Compo. Syst., 38, 786-803, 2010.
12. C. Liang, J. R. C. Juarez, “A Normalization Method for Solving the Combined Economic and Emission Dispatch Problem with Meta-Heuristic Algorithms”, Int. J. Electr. Power Energy Syst., 54, 163-186, 2014.
13. Vijay, “Intelligent Bacterial Foraging Optimization Technique to Economic Load Dispatch Problem”, Int. J. Soft Comput. Eng., 2, 55-59, 2012.
14. S. Yang, S. S. S. Hosseini, A. H. Gandomi, “Firefly Algorithm for Solving Non-Convex Economic Dispatch Problems with Valve Loading Effect”, Appl. Soft Comput., 12, 1180-1186, 2012.
15. Pothiya, I. Ngamroo, W. Kongprawechnon, “Ant Colony Optimisation for Economic Dispatch Problem with Non-Smooth Cost Functions”, Int. J. Electr. Power Energy Syst., 32, 478-487, 2010.
16. Saka, “Economic Load and Emission Dispatch Analysis at Power Systems”, M. Sc. Thesis, Gazi University, Ankara, 2017.
17. Dogan, T. Olmez, “A New Metaheuristic for Numerical Function Optimization: Vortex Search Algorithm”, Information Sciences, 293, 125-145, 2015.
18. Dogan B., T. Olmez, “Vortex Search Algorithm for the Analog Active Filter Component Selection Problem”, International Journal of Electronics and Comminications, 69, 1243-1253, 2015.
19. Saka, I. Eke, S. S. Tezcan, M. C. Taplamacioglu, “Application of Vortex Search Algorithm to Economic Load Dispatch Including Transmission Losses with Valve-Point Loading Effect” in 1st International Mediterranean Science and Engineering Congress, Adana Turkey, 2016.
20. Singh, Y. Kumar, “Economic Load Dispatch Using MRPSO with Generator Ramp Rate Limits Constraint” in Int. Con. Comp. Int. and Com. Networks, 632-637, 2012.
21. Trivedi, A. H. Ranpariya, A. Kumar, P. Jangir, “Economic Load Dispatch Problem with Ramp Rate Limits and Prohibited Operating Zones Solve using Levy Flight Moth-Flame Optimizer” in Int. Conf. Energy Efficient Technologies for Sustainability, 442-447, 2016.
22. Singh, Y. Kumar, “Economic Load Dispatch with Valve Point Loading Effect and Generator Ramp Rate Limits Constraint Using MRPSO”, International Journal of Advanced Research in Computer Engineering & Technology, 2, 1472-1477, 2013.

(Click to view)

(Click to view)

No. of Downloads Per Month

No. of Downloads Per Country