1. Introduction

This paper is an extension of work originally presented in conference MIPRO 2017 [1].

Combinatorial optimization (CO) is a research field with many important real-world applications. Scheduling [2], auctions [3], and vehicle routing [4] are just a few notable examples. Combinatorial optimization is a subfield of mathematical optimization. It deals with problems where optimal selection needs to be done from a discrete feasible set. Exhaustive search evaluates all possible solutions before selecting the best one which is infeasible for realistic problem sizes. There are special classes of CO problems that can be solved with polynomial-time algorithms such as shortest paths, flows, spanning trees, and matching. However, many interesting problems are NP-complete and for these problems, unless P=NP, there are no computationally efficient solving algorithms. For such problems, different search or metaheuristic algorithms are created in order to get as good as possible performance in a realistic amount of time. Design of such algorithms is an intrinsically empirical process, guided by the experiments while the ranking of different design choices, hyperparameter values and algorithms depends on the results from experimental runs, often performed on benchmark test sets.

Each experiment consists of experiment units which denote the smallest indivisible executable unit. Experiment units are in the focus of this paper as they tend to be independent during the execution, which enables a high degree of parallelization. In deterministic CO problems all the parameters are deterministic. For them, each sampled instance of CO problem comprises an experimental unit. In stochastic and robust CO problems, some of the parameters are uncertain or unknown. In that case, each combination of sampled problem instance with its sampled parameter scenarios makes one experimental unit.  For that reason, the number of experimental units in stochastic and robust problems can grow exponentially in the number of uncertain parameters. Additionally, the aforementioned set of experimental units is increased in Cartesian product with other experimental factors, as shown in Figure 1. Such factors include hyperparameter values, used algorithm, and algorithm design choices.

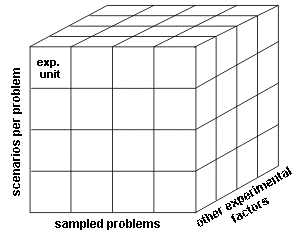Figure 1. Exponential growth of number of experimental units with added factors which constitute independent dimensions

The experiment requires execution of all experimental units and empirical data must be recorded over those runs. This can be expensive operation, depending on the number of experimental units and the complexity of the underlying problem in each unit. However, as already mentioned, experimental units tend to be computationally independent and the process of experiment execution is inherently parallelizable over the units. In the current state-of-the-art combinatorial optimization, experimentation is mostly done on single computer. This was the case in stochastic variant of vehicle routing problem in [5] and project scheduling in [6]. There were applications where the problem was of such complexity that computer cluster had to be employed in order to make the algorithm practically usable. This was the case for fleet optimization in [7].

In this paper we present an architecture of a system for distributing extensive computational experiments over the cloud that takes advantage of the independence between experimental units to achieve inexpensive scalability in the cloud. This architecture can be implemented as a standalone system or it can use some of the frameworks and systems described in section 2 if the amount of reuse and alignment of the blueprint with the implemented functionalities in those systems can be achieved. The architecture was designed in a way to reduce the amount of communication to a minimum level while still enabling efficient load balancing. We explain the distributed design of data storage for the experimental results. The distributed design reduces the communication overhead which is a problematic aspect for high-performance computing (HPC) in the cloud. Storing rich experimental data is important for further analysis and also important as a mean of scientific scrutiny by enabling efficient sampling-based reproducibility. An optimization model is presented that describes the best choice of settings for running specific experiments. The model uses data from pilot runs which execute sampled subset of experiment units. Finally, the proposed architecture was applied on a specific problem of developing and validating algorithms for a new type of complex stochastic combinatorial optimization problem in project scheduling.

The paper is organized as follows: in section 2 we present the idea of high-performance computing in the cloud as an alternative to in-house grids. Section 3 lists the related work. Section 4 presents the general architecture of our system for distributed experimental runs. In section 5, a distributed design of the storage is described. Applications of the architecture on a real research problem are described in section 6. Section 7 drafts future research ideas and section 8 offers concluding remarks.

2. High-performance computing in the cloud

Distributed computing is unavoidable in high-performance computing (HPC) where job is divided between many available processors in order to significantly reduce the runtime with currently available hardware. Traditionally, dedicated in-house grids (super-computers) are used. They are difficult to setup, maintain and operate [8]. In this paper we shall deal with cloud computing as a flexible and cheap resource alternative that can be rented on demand instead of being owned the whole time – for a lower overall cost and a relatively small performance penalty. Studies have been conducted on the matter of using the cloud for high performance computing. In [9] and [10] authors concluded that there is a limit on a number of used computational nodes where coupled applications are competitive with in-house grids. Beyond that limit, overheads become overwhelming performance detractors. In [11] virtualization, latency and system noise are singled out as the biggest issues in comparison to dedicated supercomputers. They found that research groups with limited access to supercomputer resources and with varying demand might find cloud computing to be a beneficial choice. Latency is problematic due to used commodity equipment in most of the cloud infrastructure and network virtualization. Virtualization introduces performance penalties through network virtualization and other virtualization overheads while accessing physical resources. In [11], network virtualization was found to be the primary bottleneck of the cloud that increases latency, reduces bandwidth and interferes with processes. System noise affects the performance due to multi-tenancy which introduces resource sharing with virtual machines deployed on the same physical hardware. Service providers can manipulate the degree of multi-tenancy, which enables greater profit by overallocating resources to the users. The problems with HPC in the cloud were reiterated in [12] where authors have put the focus on necessary reductions in communication overhead and virtualization. For the former, they propose the implementation of better load balancing, and using bare-metal containers for the latter. Comparative study in [13] confirmed raw performance superiority of in-house grids to Amazon’s Elastic Compute Cloud (EC2) cluster. However, waiting time in queue on HPC clusters plays a significant role when taking turnaround time into account . In such circumstances EC2 cluster could produce better turnaround times. The cost-effectiveness of running HPC application was observed as dependable on raw performance and scalability. Cloud computing enables utilizing available monetary resources to rent practically as many as possible identical processing instances. This identicality of processing instances is desirable in running experiments as it sets all runs in the identical environment. This keeps most of the variance in measurements related to designed experimental factors. The effect of system noise on experiment results can be reduced using effective randomization in the job balancing.

3. Related work

In the last decade, with advent of Big Data, usage of cloud computing became all-pervasive. Related to scientific applications, authors in [14] presented a reproducible genome sequencing task that was run in the cloud for a small cost with a near linear scalability. In [15], a new artificial intelligence algorithm for complex control tasks has been created. It features linear speedups with over a thousand workers on a public cloud service to cut down on total execution time in comparison to other algorithms. Authors in [16] have created distributed architecture for deep neural networks in the cloud for sensor fusion and inference based on the data from multitude of end devices. The communication cost was reduced by a factor of over 20x compared to the alternative. All of the aforementioned applications intentionally achieved low communication requirements between subtasks, hence avoiding or mitigating problems related to the communication overhead in cloud computing. Distributed execution engines have been created to simplify parallelization of computationally intensive tasks. Ray [17] is a python-based example of such system which enables computations.

 Existing tools that provide support in design and comparison of optimization algorithms are listed in this paragraph. Comparing Continuous Optimizers (COCO) [18] is a platform for continuous optimization, hence it does not cover combinatorial optimization. Nevertheless, it has many of the features needed in a tool for our needs. It has a library of standard benchmark problems on which optimizers can be compared. Experiments can utilize Shared Memory Parallelism (SMP), but grid computing is not utilized. For that reason, big-scale execution in the cloud is not standard feature of that platform. ParadisEO [19] is a white-box C++ framework for reusable design of parallel and distributed metaheuristics. It has features and components helpful for creating new algorithms. The intent of this framework is to simplify the design of topologies within a single running system, i.e. a single optimizer that can be distributed. However, it does not specify the efficient way of executing distributed experiments. Java Evolutionary Computation Toolkit (ECJ) [20] is an option similar to ParadisEO. Multi-Objective Evolutionary Algorithm (MOEA) [21] Java-based Framework deals with multi-objective optimization by combining the features of COCO, ParadisEO, and ECJ. We have pointed out that COCO covers only continuous optimizers, while other tools enable easier and faster algorithm design. The latter is achieved through reusability of common algorithmic components when the optimization problem and algorithm design have favorable features. These tools do not specify guidelines for distributing extensive computational experiments over the cloud.

Performance of executing the experiment in the cloud is an important issue. Predictions can be used in scheduling as well as in finding optimal settings of computational nodes. The focus of [22] is on comparing public cloud providers using measurements on specific applications. These measurements can inform the processes of provider selection and performance prediction. Performance prediction using machine learning for improving the quality of system management decisions has been investigated in [23]. Authors in [24] used machine learning to predict the execution time of computational fluid dynamics applications in the cloud. These predictions were used in scheduling algorithms. A system for efficient performance prediction for large-scale analytics on EC2 cloud has been created in [25]. It utilizes optimal experimental design in order to minimize the resources in building

the model. The system is used to find the optimal configuration in number of instances. Our architecture uses simple statistical model for performance prediction in order to calculate cost-optimal instance-type and number of necessary instances in order to satisfy desired probabilistic level of satisfying the deadline. In our case, settings also include the cloud provider, hence combining the intents of aforementioned works: performance prediction and optimization of node-selection that takes into account the cloud provider as well.

4. Architecture

The intended use-case is inherently parallelizable task. This architecture is designed in a way to use those favorable features of the task in order to achieve low communication between the computational nodes. In that way, latency is not an issue and there is only occasional communication where bandwidth plays the main role. Communication between the nodes is necessary for creating the computational nodes, sending instructions for job chunks (that is, batches) to them, and during migration of the final results. Instructions for job chunks contain small amount of information. Chunks are sized in a way to keep the nodes occupied for some time. There is a tradeoff between achieving good job balancing and reducing communication overheads in relation to the amount of computation done on the node. Computational nodes keep all generated and logged experimental data locally in their part of distributed database. The results, raw or processed, can be pooled periodically, upon finalization of the assigned experiment chunk or at the end of node’s part in the experiment. Aforementioned features make the problem suitable for cloud deployment as we can avoid communication-related detrimental effects on performance.

Our pipeline architecture includes five general stages in the experimental process:

1. Creation of experimental data, that is the data about experiment units in initial seed database.
2. Creation of node images populated with all the necessary data and optimized code for executing the experiment units, logging and storing the results.
3. Optimizing the settings of execution environment. Pilot runs are used on a small subset of experiment units for different settings of the nodes, including a service provider to inform the optimization procedure.
4. Executing the experiment on pre-calculated number of identical nodes with settings selected in the previous stage.
5. Collecting experimental data from computational nodes, conducting analysis and getting the results.

In the rest of this section, we shall describe each of the stages in more details. All steps are enumerated according to their corresponding figures.

4.1.  Creation of the experimental data

The data needed for running an experiment is created in the first phase, which is depicted in Figure 2. This means creating all the data that sufficiently describes experiment units so that they can be created and executed.

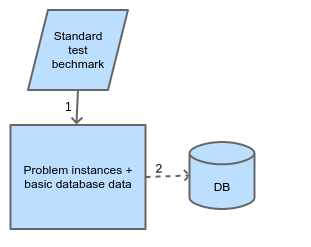Figure 2. Preparing the seed database

The first step in this stage is optional. It uses standard test set as a source for creating problem instances. For many well-researched CO problems, such sets are shared within the community of the researchers to enable consistent ranking of algorithms. In case of new CO problems, maybe a standard test benchmark related to the problem can be found and used for creation of problem instances. Also, problem-instance generators are available for some problems and custom test set can be created. In this step, sampling and transformations of problem instances can be done to create our own set of problem instances that are going into an experiment.

Actually used test set is created at this point. The “seed” database is created and populated with the metadata necessary for experiment execution. Also, it is filled with all the data about experiment units needed for execution and result logging. Part of the data can be in the form of external files if that is more appropriate, but they must be linked from a database. In order to enable distributed execution, a database (and external data) is distributed over the nodes in such a way that each node has its independent, unsynchronized version of a database. Each such database is initiated from a singular seed database. Horizontal fragmentation of writeable relations is employed as a mean of data distribution over the nodes. Details of a database are given in section 5.

4.2.  Creation of node images

One or more virtual machine (VM) images need to be created at this stage (shown in Figure 3). The exact number depends on the requirements in a phase of pilot runs. Each image contains a copy of a seed database and all the necessary code for running the experiment chunks on the node. Executable code is tuned to the intended hardware. After that, image is migrated to the cloud service from where it can be easily deployed for creation of the computational nodes.

4.3.  Optimizing the execution environment

It is hard to know exactly in advance what settings of the computational node are efficient. For that reason we need an optimization phase of an experiment with regards to the settings of the experiment run. This is a stochastic combinatorial optimization problem as well and it can be stated as a problem of minimizing the monetary cost of renting cloud instances under a constraint of

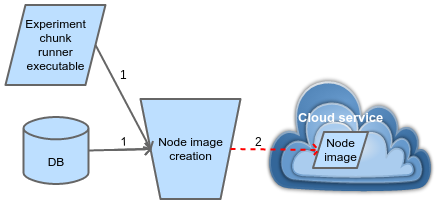Figure 3. Creating the image for virtual machines in computational nodes

achieving desired probability of finishing before the selected deadline. The problem can be formulated and expressed as:

                          min E ∑_xÎS C_x(n_x)                                (1)

with the constraints:

                                ∑_xÎS δ_x=1,                                       (2)

                          P{T_x(n_x)£D}≥δ_x×p, “xÎS,    (3)

                  δ_xÎ{0,1}, “xÎS,                          (4)

                             n_xÎN₀, “xÎS.                                    (5)

In the above formulation E is the expectation operator and P is a probability measure of the set. The above problem (1)-(5) has several parameters with values known prior to optimization: D is a desired deadline, S is a set of node-type options, and p is a desired probability of achieving the deadline. Also, C_x is a random cost of running the experiment on n_x instances of node-type x. The cost is random as it depends on the utilization durations of n_x nodes. T_x is a random experiment finish time when running it on n_x instances of node-type x. Decision variables are n_x and δ_x where n_x represents a number of instances of type x (5), and δ_x represents exclusive choice between the node-types (4). Randomness in this problem originates from the noise in execution due to hardware reasons and uncertainty in computational requirements of each experiment unit. That randomness is reflected in C_x and T_x. These functions can be created using statistical analysis or machine learning on the data from pilot runs. The objective function (1) is the expected value of total cost of the experiment. It sums the costs across all possible node-types but only one of those costs is going to be non-zero. The first constraint (2) ensures that only one node-type is selected. A set of chance-constraints (3) ensures that for selected node-type x a number n_x of nodes is selected so as to achieve a desired level of safety. All zero-valued δ_x make these constraints trivially satisfiable for all non-selected node-types x. For the selected node-type, a constraint enforces that a probability of finishing before the deadline must not be lower than the prescribed p.

We propose to make a parameter search over a set of node settings by running a simple and small experiment (using only a subset of experiment units) on each setting in S. A set of options should be small in order to reduce the cost of doing the pilot runs. That set can be composed by a careful pre-selection based on available data from previous general analyses such as [22] and based on analysis of the code for experiment execution as in [26].

The settings with the most impact are the selected cloud-service provider and cloud-instance type. The latter can be further customized across some set of subsettings, but usually the types are predefined less flexibly. The most important subsettings pertain to hardware components: CPU, disk size, RAM, etc. Pilot runs are identical to executing the experiment described in the following subsection. The difference from the latter is in the scale; in pilot runs just one experimental node per different setting is used , while many experimental nodes with identical settings are used during the experimental run. Collected data are analyzed by a procedure described in subsection 4.5. Based on the collected data and optimization model, economically most efficient node setting is chosen for the full experiment. Also, for that choice we get an estimate of the total experiment run time and cost by taking the summary statistics of T_x and C_x. Based on a desired due date, we infer the necessary number of computational instances N. N is the value of only non-zero n_x in optimal solution of the the optimization model.

4.4.  Executing the experiment

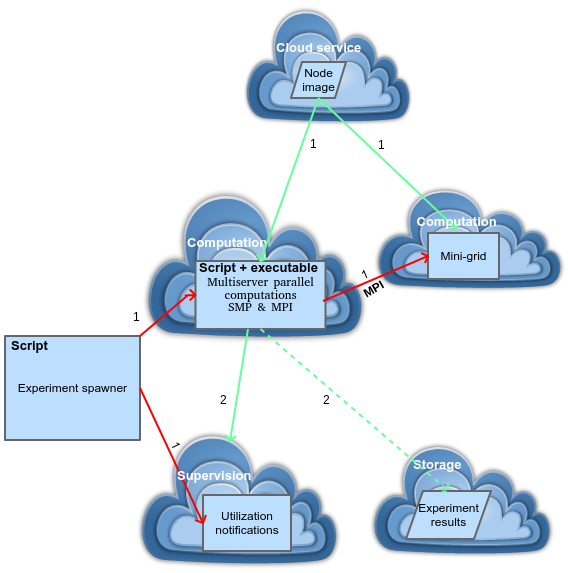Figure 4. Execution of the experiment

The experiment is executed by distributing chunks across computational nodes (Figure 4). Experiment spawner is a script that balances the load between instantiated computational nodes. The experiment is partitioned into disjoint experimental chunks. Each chunk is a set of experiment units to be executed on a single computational instance.

1. Experiment spawner creates N cloud nodes and sends over network the parameters that define their workload chunks. These parameters constitute a small amount of information. Each experimental node runs a chunk runner which processes its assigned workload. Each runner, depending on the type of a problem, can instantiate additional computational nodes to form a mini-grid using Message Passing Interface (MPI). That is done if some of the algorithms require such execution architecture by design. SMP can be switched on by the parameters sent from the experiment spawner. Each node sets triggers for utilization alarms at the performance supervisor. Triggers improve the efficiency of a system by notifying the subscribers of different events. This information can be used for better, more prompt load balancing and it can reduce the renting costs.
2. At the end of processing a chunk, a computational node triggers supervisor’s alarm when it can get another chunk to execute. When the node finishes with processing, it migrates its results to a permanent cloud storage and it gets terminated.

4.5.  Result analysis

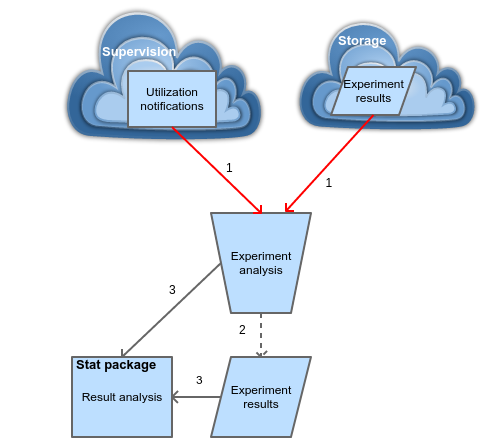Figure 5. Analysis of experimental results

Users are notified by supervisor’s alarm about the finalized jobs. A procedure is subscribed to notifications and reacts to them as shown in Figure 5. At first, the data is migrated from a computational node to some storage, locally or in the cloud. If the node has no more jobs to process, it is terminated to reduce costs. Analysis is done iteratively over the partial data as they pool to the storage. At the end of the process, with all the experimental results available, concluding results are created.

5. The database

The main objective of our system is to produce detailed experimental data as fast as possible. We have decided to store all the data into a database as it simplifies manipulations with overwhelming amounts of data.

It is assumed that running computational experiments is expensive both temporally and monetary. Storage, on the other hand, is much cheaper on both accounts. For that reason, as much data as possible should be stored for future analyses to avoid experiment re-runs.

Practicing scrutiny is important in science in order to prune mistakes and misconduct. Replication studies simply repeat experiments to check if the results match. In computer science, this can be done by sampled replications that repeat small sampled set of experiment units. In each repetition, the same settings for pseudo-random number generators (PRNG), algorithms and problem instances should be used to create near-identical conditions as with the initial experiment. The results of replication study must match the stored values for everything except the execution time which includes incontrollable system noise. This is more efficient than replications of physical experiments where the exact conditions cannot be repeated and results should only statistically match. In the latter case, a greater number, if not all, of experimental units needs to be repeated in order to make conclusions. Also, executing experiment units in computational experiments is often cheaper than for physical experiments. The probability of non-matching results gets exponentially smaller with the size of randomly generated sample for replication.

5.1.  Design

As described in section 2, communication overheads are serious performance detractors to scalability in the cloud in comparison to the in-house grids. Grids have tight interconnection and synchronization. For that reason, we have decided to minimize communication frequency between the cloud instances. All instances have their own database for storing results that springs from the initial seed database which is copied to all instances during creation of the node image as described in subsection 4.2. Seed database holds metadata and identification/replication data. The former defines all necessary structures to store the experiment data. The latter are the basic data necessary for identification of experiment units. Such data include the shared information for all instances of CO problems, used optimization algorithms, PRNG types and uncertainty scenarios in the case of stochastic or robust CO. Hence, all the data that define and describe experiment units (Figure 1) are present in a seed database.

Each node is created with a separate copy of a seed database. These copies make up a distributed database. The writeable relations, which record the experimental run data, are horizontally fragmented. Horizontal fragmentation keeps table schemas and distributes table rows across the nodes, as depicted in Figure 6.

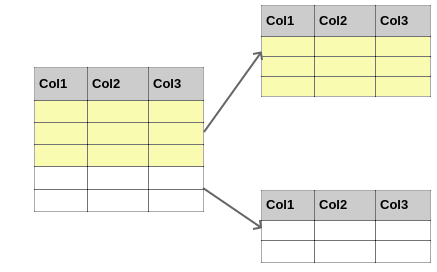Figure 6. An illustrative example of horizontal fragmentation

During the experiment execution, each node saves two types of data: identification/replication data, and performance data. The former describe the settings of an executed experiment unit. This consists of the settings of the used optimization algorithm, PRNGs and other components that hold the key to replicating the execution of the experimental unit during replication studies. Performance data track decisions made during the execution and measurements of their effects. Quantitatively they make up the majority of generated and stored data, and the final conclusions are based on them.

Distributed data uses the identification scheme that combines together node-specific identification/replication information with shared information that originated from a seed database. That scheme makes data aggregation from all chunks unambiguous.

6. Application

The primary motivation for creating previously described architecture was a practical problem. As a result of different branch of research, we have worked with the new type of stochastic project scheduling problem, Cost-based Flexible Stochastic Resource Constrained Project Scheduling Problem (CBF-SRCPSP), defined in [27]. This problem deals with proactive-reactive project scheduling which makes the synchronization between project collaborators easier. It uses an agreed upon baseline schedule that stores the time-agreements for starting times of different project activities. Deviations of real start times from these agreements are penalized for inflexible, change-sensitive activities. The additional element in this model is that the changes to the baseline schedule can be profitable if they can be undertaken sufficiently far into the future. This extension to the features of baseline schedule makes the solution space much more complex due to the aforementioned proactive rescheduling operations. Searching the solution space becomes more time-consuming, though it pays off. We were lead empirically through the design and creation of optimization algorithms for CBF-SRCPSP.

The experimental set was created based on the standard Project Scheduling Problem Library (PSPLIB) set of instances for deterministic resource constrained project scheduling problems [28]. Cluster sampling was used to select sets of template instances from J30, J60, and J120 problem sets. The latter consist of projects that have 30, 60, and 120 project activities, respectively. The templates were expanded to fit CBF-SRCPSP model by modeling the stochasticity in activity durations with discretized beta distributions with a combination of selected and randomly generated distribution parameters. Additional parameters for each activity were randomly generated, according to the selected triangular distributions. After this procedure we ended up with 300 instances of each size which sprang up from template instances extended to fit the new model. The templates were instantiated according to the two experimental factors regarding to the project deadline: tightness of the deadline and bonus for early-finishing the project. For each instance, we generated 1000 activity duration scenarios from the discretized beta distributions. Activity durations were the only source of uncertainty. All of this data: project instances and uncertainty scenarios per each project were fed into a seed database. The used database was sqlite3 as it fit the needs of our experiment. Its simplicity trades-off well with its shortcomings in comparison to the more elaborate database management systems.

The seed database was also populated with the metadata about used PRNGs and CO algorithms. We have used two PRNGs: Mersenne twister with careful parameterization [29] and Threefry [30]. Several search algorithms were developed during the algorithm design. We had at our disposal implementations of optimization algorithms from the CO literature that were already available in the used simulation library [26]. The final experiment included one benchmark CO algorithm from the literature and two selected newly-developed algorithms that were hypothesized to significantly outperform the benchmark. However, the analysis necessary for proving the hypothesis necessitated sufficient number of samples. The newly-developed algorithms were computationally expensive due to a search in more complex solution space than the benchmark.

The node images used Linux with gcc and necessary libraries. New algorithms were developed upon the C++ simulation library from [26]. This means that the most computationally intense parts, namely simulation-based experimentation and database logging were coded in C++ for better performance. The mini-grids were not used, since all the algorithms used only shared memory parallelization with two threads using OpenMP to speed up the search. This choice was based on the experiment in [26] regarding the parallel efficiency of the used simulation library. That also determined the number of computational cores per instance.

The total experiment was run on two occasions. The second experiment was done due to improvements to the developed algorithms and the results from the second study were used in the final experiment report. Here we shall cover both experiment runs as they utilized different experimental choices. In both cases, the raw results were downloaded locally using the python script. Statistical language R was used for results analysis. RSQLite R package was used to query the databases for the relevant data and to gather them together from all the sources.

6.1.  The first experimental run

During the first experiment run we have selected Amazon Web Services (AWS) [31] as a service provider. Therefore, we did not use service provider as the experimental factor in pilot runs during the selection of the ideal instance type. We have used EC2 for computations, and have opted, after pilot runs, for c3.large instances with 2 dedicated physical cores of Intel Xeon E5-2680 v2 (Ivy Bridge) processors and 3.75 GiB of RAM. Simple Storage Service (S3) was used to store experimental results. The combination of CloudWatch (CW) and Simple Notification Service (SNS) was used for supervision and utilization notifications. Experiment spawner was coded in python, using the boto API [32] for accessing AWS and paramiko module [33] for controlling SSH2 connections.

Experiment consisted of 1.6 million experiment units. Experiment chunking was done across the problem instances. The chunk runner accepts parameters that describe chunk boundaries. These parameters are just several bytes in size and it is all the information needed for initiating the experiment execution on a computational instance. The total computational workload of the experiment was estimated based on running small sample of experiment units during the pilot run. It was estimated that the total workload is three and a half months of computational labor on the available hardware. The deadline was set to 7 days which we wanted to achieve with 90% probability. We calculated the necessary number of computational instances to satisfy this requirement.  This resulted in using up to 26 cloud instances and reducing the total duration to 6 days. The database for each instance was migrated to S3 at the end of chunk execution and it awaited further analysis there. The cost of the first experiment was 445$.

6.2.   The second experimental run

The second experiment was run on improved algorithms. The number of the most computationally expensive units was significantly increased, resulting in the total of 2.1 million experimental units. The optimization stage was used to select the node-type, also taking into account the service provider. We have used prior knowledge of the characteristics of our experiment runner – low working memory consumption (under 500MB) and high CPU utilization – to narrow down a range of instances. We tested the instances with 2 processors and as close as possible to 2GiB of memory. Market research was used to select the small set of service providers: Online Virtual Hosting (OVH), AWS (due to the use in the first experiment), and Linode. The selected instance-types are listed in Table 1.

Table 1. Members of alternative set S for optimization of execution environment

	OVH	Amazon EC2	Linode
instance-type	2vCores@ 2.4GHz 8GB RAM	c3.large 2vCores@ 2.8GHz 3.75GB RAM	2vCores@ 2.5GHz 4GB RAM
price	13.49$ (monthly)	0.105 $(hourly)	20$ (monthly)

The identical pilot run was used on all instance-types. Seven different types of experiment units were sampled into the pilot’s unit set. The price of pilot runs in the optimization stage was 1.1$. The measurements were used to model execution durations for each combination of instance-type x and unit type u as Gaussian random variables d_x,u. Then, the total experiment duration for each instance-type is Gaussian random variable where w_u is the number of units of type u in our experiment. We approximated T_x by assuming that the total work modeled by d_x is simply equally divided among n_x computational instances.

It was estimated with the probability of 90% for the fastest option that the total workload is just above three years. The ranking and the necessary number of instances were calculated in order to satisfy the selected deadline of 30 days with the probability of 90%. The deadline was set to 30 days to take advantage of the monthly pricing. Figure 7 shows the optimal expected total costs for each option in Table 1. The results in Figure 7 were anonymized due to the legal concerns. Based on the available data, we have selected the C3 type instance as the most efficient with the estimated cost just below 500$. The experiment was run and it finished after 23 days of executing.

7. Future work

Possible future research ideas include improvement to the robustness of the total workload estimator. In our application, different simplifying assumptions were made and the error of their approximation effect should be investigated.

In order to reduce costs of the research community, general data about computational experiments (duration and prices) could be shared online with the public. This data can be useful for creating promising and efficient alternative sets for optimizing the execution environment.

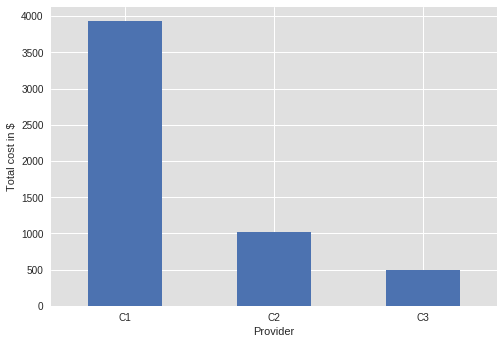Figure 7 Estimates of total expected cost for anonymized permutation of options from Table 1

An automated tool for the composition of alternative sets could be utilized based on the experiment requirements. There is a potential in using pilot run on just one carefully selected instance type and then utilizing machine learning to find the best option and the number of necessary instances N for the desired target duration and the probability of achieving it. More advanced notions of risk and chance constraints can be used to account for the uncertainty in estimations and its economic effect. That can inform budget planning and the project management that undertakes the experiment.

Many parts of the architecture presented in section 4 are abstracted from the details of the particular experiments and can be reused in different settings. Component-based framework for general experimenting can be created. In that way, reuse of existing components can be increased and a code generator for repetitive parts can speed up the development, especially if the user does most of the manual process through an intuitive graphical user interface. Cloud costs can be reduced further by better node tracking and possibly using the cheaper spot instances for non-critical computations, especially during the algorithm design, prototyping and various pilot runs. The performance penalty in case of using such instances should be investigated in order to drive recommendations for configurations that utilize them.

8. Conclusion

Cloud computing is still not a simple and clear choice for high performance computing due to the issues pointed out in [11]: communication overhead, virtualization and system noise. The efficiency of cloud depends greatly on the specifics of the problem that we are trying to solve.

We have presented a system for distributing combinatorial optimization experiments over the cloud. Doing computational experiments for validation and guiding the design of CO algorithms has a specific property that it can be parallelized across experimental units that tend to be independent. This allows for low coupling between the simultaneous tasks and circumvents the issues related to the communication overhead.

Our system records rich data about the experimental runs in order to reduce the need for re-runs of experiments which may be computationally and monetarily expensive. In order to keep communication overhead to the minimum, distributed database with horizontal fragmentation was used. Each cloud node populates only the data related to its assigned disjoint experiment chunk. The unambiguity of the data across the system is, hence, kept without additional effort. When the tested algorithms use distributed computations in mini-grids, they should keep the grid size within the limits of recent studies, such as given in [11], to get the best performance benefits. It is expected that additional tuning and advances in cloud computing technology will increase the limits found by these studies.

We described two successful applications of our proposed system on the newly developed algorithms for complex stochastic combinatorial optimization problem, CBF-SRCPSP. Initial estimated sequential duration of several months to several years was reduced to under a month (the first experiment under a week) by distributing the execution. The optimization stage of our architecture finds the best settings for the execution environment. This enables the selection of the best instance-type across different cloud-service providers. In our case, that significantly reduced the cost of running the experiment.

Conflict of Interest

The authors declare no conflict of interest.

1. Brcic and N. Hlupic, “Cloud-distributed computational experiments for combinatorial optimization,” in 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2017, pp. 197–201., http://doi.org/ 10.23919/MIPRO.2017.7973417
2. Westphal, “Scheduling the German Basketball League,” Interfaces, vol. 44, no. 5, pp. 498–508, Oct. 2014.
3. Sheffi, “Combinatorial Auctions in the Procurement of Transportation Services,” Interfaces, vol. 34, no. 4, pp. 245–252, Aug. 2004.
4. Kant, M. Jacks, and C. Aantjes, “Coca-Cola Enterprises Optimizes Vehicle Routes for Efficient Product Delivery,” Interfaces, vol. 38, no. 1, pp. 40–50, Feb. 2008.
5. C. Goodson, J. W. Ohlmann, and B. W. Thomas, “Rollout Policies for Dynamic Solutions to the Multivehicle Routing Problem with Stochastic Demand and Duration Limits,” Oper Res, vol. 61, no. 1, pp. 138–154, Jan. 2013., http://dx.doi.org/10.1287/opre.1120.1127
6. Lamas and E. Demeulemeester, “A purely proactive scheduling procedure for the resource-constrained project scheduling problem with stochastic activity durations,” J. Sched., vol. 19, no. 4, pp. 409–428, Aug. 2016., http://doi.org/ 10.1007/s10951-015-0423-3
7. P. Simão, A. George, W. B. Powell, T. Gifford, J. Nienow, and J. Day, “Approximate Dynamic Programming Captures Fleet Operations for Schneider National,” Interfaces, vol. 40, no. 5, pp. 342–352, Jul. 2010., http://doi.org/ 10.1287/inte.1100.0510
8. Vecchiola, S. Pandey, and R. Buyya, “High-Performance Cloud Computing: A View of Scientific Applications,” in 2009 10th International Symposium on Pervasive Systems, Algorithms, and Networks, 2009, pp. 4–16., http://doi.org/ 10.1109/I-SPAN.2009.150
9. Evangelinos and C. N. Hill, “Cloud Computing for parallel Scientific HPC Applications: Feasibility of Running Coupled Atmosphere-Ocean Climate Models on Amazon’s EC2,” in In The 1st Workshop on Cloud Computing and its Applications (CCA), 2008.
10. Kondo, B. Javadi, P. Malecot, F. Cappello, and D. P. Anderson, “Cost-benefit analysis of Cloud Computing versus desktop grids,” in 2009 IEEE International Symposium on Parallel Distributed Processing, 2009, pp. 1–12., http://doi.org/ 10.1109/IPDPS.2009.5160911
11. Gupta et al., “The Who, What, Why, and How of High Performance Computing in the Cloud,” in 2013 IEEE 5th International Conference on Cloud Computing Technology and Science, 2013, vol. 1, pp. 306–314., http://doi.org/ 10.1109/CloudCom.2013.47
12. Tomić, Z. Car, and D. Ogrizović, “Running HPC applications on many million cores Cloud,” in 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2017, pp. 209–214., http://doi.org/ 10.23919/MIPRO.2017.7973420
13. Marathe et al., “A Comparative Study of High-performance Computing on the Cloud,” in Proceedings of the 22Nd International Symposium on High-performance Parallel and Distributed Computing, New York, NY, USA, 2013, pp. 239–250., http://doi.acm.org/10.1145/2462902.2462919
14. S. Shringarpure, A. Carroll, F. M. D. L. Vega, and C. D. Bustamante, “Inexpensive and Highly Reproducible Cloud-Based Variant Calling of 2,535 Human Genomes,” PLOS ONE, vol. 10, no. 6, p. e0129277, Jun. 2015., http://doi.org/ 10.1371/journal.pone.0129277
15. “[1703.03864] Evolution Strategies as a Scalable Alternative to Reinforcement Learning.” [Online]. Available: https://arxiv.org/abs/1703.03864. [Accessed: 10-Sep-2017].
16. Teerapittayanon, B. McDanel, and H. T. Kung, “Distributed Deep Neural Networks Over the Cloud, the Edge and End Devices,” in 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), 2017, pp. 328–339., http://doi.org/10.1109/ICDCS.2017.226
17. “Ray — Ray 0.2.0 documentation.” [Online]. Available: http://ray.readthedocs.io/en/latest/. [Accessed: 11-Sep-2017].
18. Hansen, A. Auger, O. Mersmann, T. Tusar, and D. Brockhoff, “COCO: A Platform for Comparing Continuous Optimizers in a Black-Box Setting,” ArXiv160308785 Cs Stat, Mar. 2016.
19. Cahon, N. Melab, and E.-G. Talbi, “ParadisEO: A Framework for the Reusable Design of Parallel and Distributed Metaheuristics,” J. Heuristics, vol. 10, no. 3, pp. 357–380, May 2004., http://doi.org/ 10.1023/B:HEUR.0000026900.92269.ec
20. R. White, “Software review: the ECJ toolkit,” Genet. Program. Evolvable Mach., vol. 13, no. 1, pp. 65–67, Mar. 2012., http://doi.org/ 10.1007/s10710-011-9148-z
21. “MOEA Framework, a Java library for multiobjective evolutionary algorithms.” [Online]. Available: http://moeaframework.org/index.html. [Accessed: 05-Feb-2017].
22. Li, X. Yang, S. Kandula, and M. Zhang, “CloudCmp: Comparing Public Cloud Providers,” in Proceedings of the 10th ACM SIGCOMM Conference on Internet Measurement, New York, NY, USA, 2010, pp. 1–14., http://doi.acm.org/10.1145/1879141.1879143
23. S. Ganapathi, “Predicting and Optimizing System Utilization and Performance via Statistical Machine Learning,” University of California at Berkeley, Berkeley, CA, USA, 2009.
24. N. Hieu, T. T. Minh, T. V. Quang, B. X. Giang, and T. V. Hoai, “A Machine Learning-Based Approach for Predicting the Execution Time of CFD Applications on Cloud Computing Environment,” in Future Data and Security Engineering, 2016, pp. 40–52., http://doi.org/ 10.1007/978-3-319-48057-2_3
25. Venkataraman, Z. Yang, M. Franklin, B. Recht, and I. Stoica, “Ernest: Efficient Performance Prediction for Large-scale Advanced Analytics,” in Proceedings of the 13th Usenix Conference on Networked Systems Design and Implementation, Berkeley, CA, USA, 2016, pp. 363–378.
26. Brčić and N. Hlupić, “Simulation library for Resource Constrained Project Scheduling with uncertain activity durations,” in 2014 37th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2014, pp. 1041–1046., http://doi.org/ 10.1109/MIPRO.2014.6859722
27. Brčić D. Kalpić, and M. Katić, “Proactive Reactive Scheduling in Resource Constrained Projects with Flexibility and Quality Robustness Requirements,” Comb. Optim., pp. 112–124, Aug. 2014., http://doi.org/ 10.1007/978-3-319-09174-7_10
28. Kolisch and A. Sprecher, “PSPLIB – A project scheduling problem library: OR Software – ORSEP Operations Research Software Exchange Program,” Eur. J. Oper. Res., vol. 96, no. 1, pp. 205–216, Jan. 1997.
29. Matsumoto and T. Nishimura, “Dynamic Creation of Pseudorandom Number Generators,” presented at the Proceedings of the Third International Conference on Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing, 1998, pp. 56–69.
30. K. Salmon, M. A. Moraes, R. O. Dror, and D. E. Shaw, “Parallel random numbers: As easy as 1, 2, 3,” in High Performance Computing, Networking, Storage and Analysis (SC), 2011 International Conference for, 2011, pp. 1–12., http://doi.org/ 10.1145/2063384.2063405
31. “Amazon Web Services (AWS) – Cloud Computing Services,” Amazon Web Services, Inc. [Online]. Available: //aws.amazon.com/. [Accessed: 14-Dec-2014].
32. “boto GitHub repository,” GitHub. [Online]. Available: https://github.com/boto/boto. [Accessed: 29-Sep-2014].
33. “Welcome to Paramiko! — Paramiko documentation.” [Online]. Available: http://www.paramiko.org/. [Accessed: 25-Oct-2017].

(Click to view)

(Click to view)