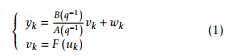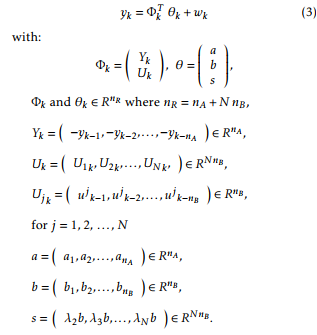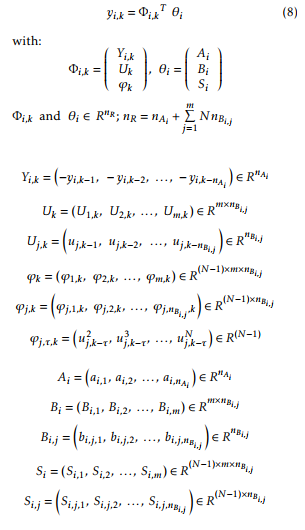1. Introduction

This paper is an extension of work originally presented in Conference on Science of Electronics, Technologies of Information and Telecommunications (SETIT 2016) [1]. The latter work presented two methods of parametric identification of decoupled multivariable Hammerstein model. It consists of one nonlinear static block and one linear dynamic block. Many process (chemical and biological process, signal processing, etc.) have this structure, for example: pH neutralization processes [2], polymerization reactor [3], distillation columns [4] and dryer process [5].

Many system identification methods have been used to identify the single-input single-output (SISO) model. They can be divided into stochastic methods [6,7], iterative methods [8], over-parameterization methods [9], separable least squares methods [10,11], blind identification methods [12] and frequency domain methods [13].

It is possible to transform the SISO Hammerstein model to MISO and MIMO model which is linear in the parameters [14]. Serval approches have been proposed to identify MIMO Hammerstein model. In [15,16,17], neuronal networks and fuzzy logic have been used to deal with more general nonlinearities. An approach based on multivariable cardinal cubic spline functions to model the static nonlinearities have been proposed in [18]. The Least Squares Support Vector Machines (LS-SVMs) have been presented in [19,20]. A generalized Hammerstein model consisting of a static polynomial function in series with time-varying linear model is developed in order to model the Hammerstein-like multivariable processes whose linear dynamics vary over the operating space in [21]. In this work, we propose a new coupled structure identification of MIMO model with separate nonlinearities. It is organized as follows: SISO Hammerstein system is presented in part 1 of section 2. A new coupled structure for MIMO Hammerstein system is developed in part 2 of section 2. Simulation results of a quadruple-tank process is given in section 3. Finally, a conclusion is made.

2. Parametric identification of Hammerstein model

2.1     Parametric identification of SISO Hammerstein model

Assume that the Hammerstein model of Figure 1 is composed of a nonlinear block F(.) associated with a

B(q⁻¹)

linear sub-system A(q₋₁₎. It is described by:

with:

Aq−1 = 1+a1q−1 +a2q−2 +…+anAq−nA

Bq−1 = b1q−1 +b2q−2 +…+bnBq−nB vk = λ1 uk +λ2 uk2 +…+λN ukN

q⁻¹ delay operator, u_k input of the system, y_k output, v_k the unmeasurable internal signal and w_k represents the modeling error, external disturbances, etc.

In order to have a unique parameterizations of the Hammerstein model structure, the first coefficient of the nonlinear function F(.) equals to 1, λ₁ = 1 [11,22].

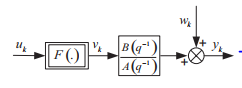Figure 1: SISO Hammerstein model

The output y_k is given by:

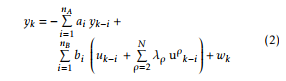Equation (2) can be written in the following form:

The parameter vector θ can be estimated using the RLS algorithm. It is described by the following equations: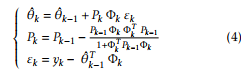

2.2     Parametric identification of MIMO Hammerstein model

where P_k is the adaptation gain matrix, Φ_k is the observation vector and θ_k is the parameters vector.

Two structures are used to identify MIMO Hammerstein models in the literature: with separate nonlinearities [21] or with combined nonlinearities [23]. The second case is the most general, but it can cause a very challenging parameter estimation problem because of the large number of parameters to be estimated.

In this paper, we developed a new coupled structure for MIMO Hammerstein model with separate nonlinearities. They are presented in Figure 2 and 4 where u_j, v_i,j, y_i for i = 1, 2,…,p and j = 1, 2,…,m are the system input, internal signal and system output. F_i,j (.) are nonlinear function.

2.2.1     A decoupled structure identification of MIMO Hammerstein model

The decoupled structure of MIMO Hammerstein model is given in Figure 2. Each output y_i,k, i = 1, 2, …p, of the multivariable system corresponds to a linear model, which at its input are introduced a nonlinear functions, Figure 3.

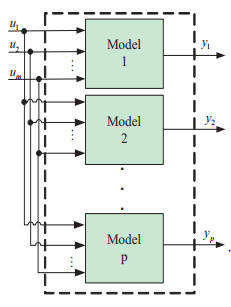Figure 2: Decoupled structure of MIMO Hammerstein model

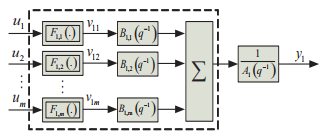Figure 3: Structure of first model

Each output y_i,k, i = 1, 2, …p, of the MIMO Hammerstein model is proposed as: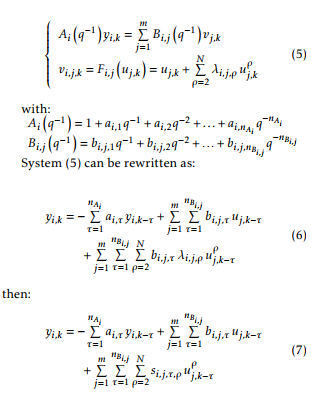

Equation (7) can be written in the following form:

The steps of the identification scheme are summarized as follows:

1. choosing an initial values for the adaptation matrix,
2. acquiring the input and output of the systemand form the vector data as shown in (11) using the present and past values of the input u, output y, and u power,
3. solving the estimate parameter A_i, B_i and S_i using the algorithm RLS,
4. solving λ_i,j,ρ using the estimated values b_i,j,τ and s_i,j,τ,ρ as:

2.2.2     A new coupled structure identification of MIMO Hammerstein system

The structure of this method is given in Figure 5. Each output of the system is depended on inputs and all other system outputs, Figure 4.

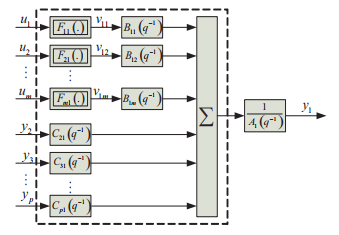Figure 4: Structure of first model

Each output y_i,k, i = 1, 2, …p, of the MIMO Hammerstein model is described by:

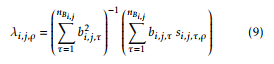
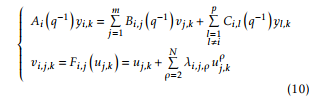
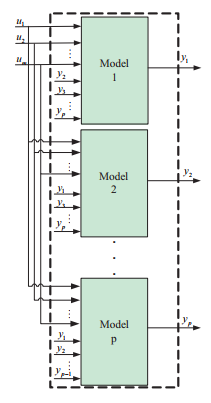Figure 5: A proposed structure of MIMO Hammerstein model

System (10) can be rewritten as:

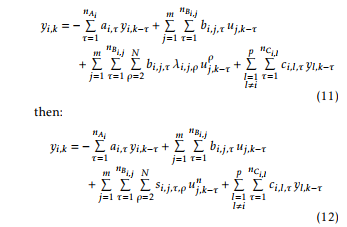Equation (12) can be written in the following form: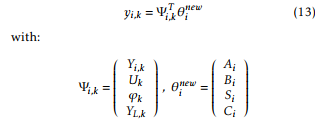

3.  Application quadruple-tank process

Parametric identification consists to determine the parameters of the system based on vectors of inputs and outputs, using the recursive least squares algorithm.

A quadruple-tank process is used to illustrate the performance of the proposed structures of the MIMO Hammerstein model.

3.1        System description

The system setup is a model of a chemical plant fragment. Very often tanks are coupled through pipes and the reactant level and flow has to be controlled. The type of the experiments was performed on the 33-041 Coupled Tanks System of Feedback Instruments [24]. This plant, a variant of the quadruple tank process originally proposed in [25], is a model of a fragment of a chemical plant, Figure 6.

Figure 6: Plant of four coupled tanks [26]

The line diagram of the reservoir system is shown in Figure 7. The coupled tanks unit consists of four tanks placed on a rig. Another reservoir tank is placed at the bottom. In the reservoir two submersible pumps are placed, which pump the water on command to the tanks. The water flows freely to the bottom tanks through the configurable orifice. The way the water flows through the setup can be configured in many ways with manual valves label led (MVA, MVB, MVC, MVD, MVE, MVF, MVG, MV1, MV2, MV3 and MV4).

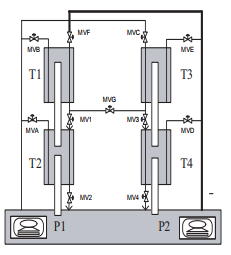Figure 7: Line diagram for quadruple-tank process

3.2        Mathematical modelling

The quadruple-tank process admits the following nonlinear model [25] which has been assembled in simulink:

Table 1: Parameters of the plant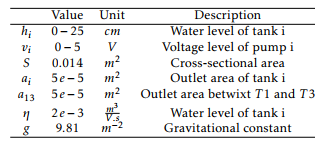

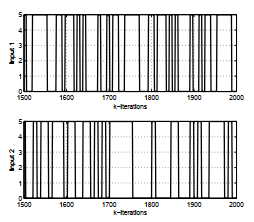
The inputs u₁ and u₂ are show in Figure 8. They are set to [0…+5V ]. The sample time used for all simulations is T_e = 1s.

Figure 8: Inputs u₁ and u₂

Solid: real, dotted: decoupled structure and doshdot: coupled structure

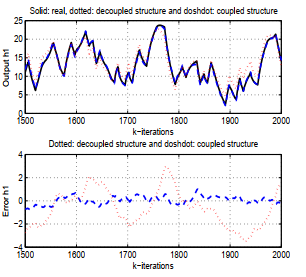Figure 9: Response of the real and estimated h₁

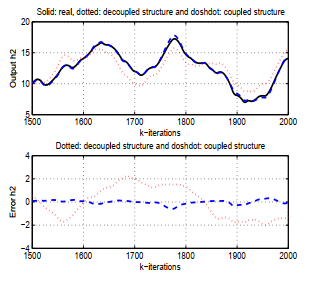Figure 10: Response of the real and estimated h₂ Figures 9 to 12 show the results of the experiments with two method from a comparative point of view.

Each of them shows a superposition of the actual output and the two outputs estimated as their two error curves. Solid line represents the real output, dotted line represents the estimated systems output signals with the decoupled structure and the dash dot lines represent the estimated systems output signals with the coupled structure in all four graphs. The responses of the original system and the results of the proposed method are very similar. It is clear that the error corresponds to the proposed structure is smaller than that corresponding to the decoupled structure. On inspection, the proposed structure is seen to work better than the decoupled structure. Thus, the feasibility and superiority of this proposed identification method are validated.

Solid: real, dotted: decoupled structure and doshdot: coupled structure

k−iterations

Dotted: decoupled structure and doshdot: coupled structure

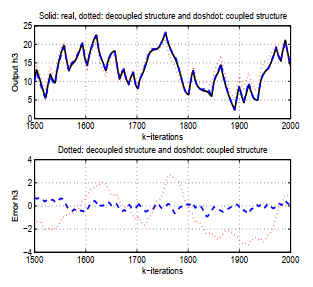Figure 11: Response of the real and estimated h₃

Solid: real, dotted: decoupled structure and doshdot: coupled structure

k−iterations

Dotted: decoupled structure and doshdot: coupled structure

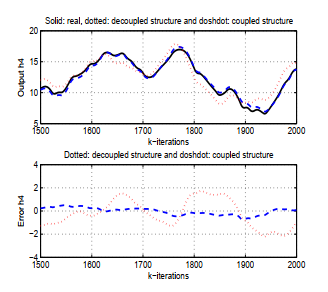Figure 12: Response of the real and estimated h₄

4. Conclusion

In this study, a new coupled structure identification of MIMO Hammerstein model with separate nonlinearities has been developed. The method is based on RLS algorithm. A comparative study using simulation results for quadruple-tank process, between the proposed structure and the decoupled structure is discussed. Simulation results reveal the performance and effectiveness of the proposed method. As a perspective, we will judge the performance of the method used in the presence of perturbations

1. Z. Rayouf, C. Ghorbel, and N. B. Braiek, “An extended identification methods for multivariable Hammerstein system” in 7th International Conference on Sciences of Electronics, Technologies of Information and Telecommunications, Hammamet Tunisia, 2016. https://doi.org/10.1109/SETIT.2016.7939921
2. Z. O. U. Zhiyun, Y. U. Meng, W. A. N. G. Zhizhen, L. I. U. Xinghong, G. U. O. Yuqing, F. ZHANG, and G. U. O. Ning, “Nonlinear model algorithmic control of a pH neutralization
   process” Chinese Journal of Chemical Engineering, 21(4), 395–400, 2013. https://doi.org/10.1016/S1004-9541(13)60479-6
3. D. Z. Li, Y. X. Jia, Q. S. Li, and Q. B. Jin, “Identification and nonlinear model predictive control of MIMO Hammerstein system with constraints” Journal of Central South University,
   24(2), 448-458, 2017. https://doi.org/10.1007/s11771-017-3447-3
4. R. Kanthasamy, H. Anwaruddin, and S. K. Sinnadurai, “A new approach to the identification of distillation column based on hammerstein model” Modelling and Simulation in Engineering, 2014(11), 1-7, 2014. http://dx.doi.org/10.1155/2014/813757
5. D. K. Rollins, N. Bhandari, A. M. Bassily, G. M. Colver, and S. T. Chin, “A continuous-time nonlinear dynamic predictive modeling method for hammerstein processes” Industrial
   and engineering chemistry research, 42(4), 860-872, 2003. https://doi.org/10.1021/ie020169
6. D. Wang, and F. Ding, “ Extended stochastic gradient identification algorithms for Hammerstein-Wiener ARMAX systems” Computers and Mathematics with Applications, 56(12),  3157–3164, 2008. https://doi.org/10.1016/j.camwa.2008.07.015
7. F. Ding, “Hierarchical multi-innovation stochastic gradient algorithm for Hammerstein nonlinear system modeling” Applied Mathematical Modelling, 37(4), 1694–1704, 2013.
   https://doi.org/10.1016/j.apm.2012.04.039
8. R. Su, B. Wang, and S. Liu, “The iterative identification method for hammerstein nonlinear channel” in 10th International Conference on Wireless Communications, Networking
   and Mobile Computing (WiCOM), Beijing, China, 2014. https://doi.org/10.1049/ic.2014.0075
9. J. Wang, Q. Zhang, and L. Ljung. “Revisiting Hammerstein system identification through the two-stage algorithm for bilinear parameter estimation” Automatica, 45(11), 2627-2633, 2009. https://doi.org/10.1016/j.automatica.2009.07.033
10. D. Westwick, and R. Kearney, “Separate least squares identification of nonlinear Hammerstein models: application to stretch reflex dynamics” Annals of Biomedical Engineering,
    29(8), 707-718, 2001. https://doi.org/10.1114/1.1385806
11. E. Bai, and M. Fu, “Identification of linear systems with hard input nonlinearities of known structure” IEEE Transactions on Signal Processing, 38(5), 853-860, 2002.
    https://doi.org/10.1016/S0005-1098(01)00281-3
12. E. Bai, and M. Fu, “A blind approach to Hammerstein model identification” IEEE Transactions on Signal Processing, 50(7), 1610-1619, 2002. https://doi.org/10.1109/TSP.2002.1011202
13. E. Bai, “Frequency domain identification of Hammerstein models” IEEE Transactions on Automatic Control, 48(4), 530-542, 2003. https://doi.org/10.1109/TAC.2003.809803
14. Y. Liu, J. Sheng, and R. Ding, “Convergence of stochastic gradient estimation algorithm for multivariable ARX-like systems” Computers and Mathematics with Applications, 59(8), 2615-2627, 2010. https://doi.org/10.1016/j.camwa.2010.01.030
15. J. Abonyi, R. Babuska, M. A. Botto, F. Szeifert, and L. Nagy, “Identification and control of nonlinear systems using fuzzy Hammerstein models” Industrial and engineering
    chemistry research, 39(11), 4302–4314, 2000. https://doi.org/10.1021/ie990629e
16. L. Jia, M. S. Chiu, and S. S. Ge, “A noniterative neurofuzzy based identification method for Hammerstein processes” Journal of Process Control, 15(7), 749-761, 2005. https://doi.org/10.1016/j.jprocont.2005.03.006
17. A. Jawad, A. M. Butt, M. T. Riaz1, S. Bhutta1, M. Z. khan, and I. U. Haq “Multiclass Myoelectric Identification of Five Fingers Motion using Artificial Neural Network and Support
    Vector Machine” Journal of Advances in Science, Technology and Engineering Systems, 2(3), 1026–1033, 2017. https://doi.org/10.25046/aj0203130
18. K. H. Chan, J. Bao, and W. J. Whiten, “Identification of MIMO Hammerstein systems using cardinal spline functions” Journal of Process Control, 16(7), 659-670, 2006.
    https://doi.org/10.1016/j.jprocont.2006.01.004
19. I. Goethals, K. Pelckmans, J. A. Suykens, and B. De Moor, “Identification of MIMO Hammerstein models using least squares support vector machines” Automatica, 41(7), 1263–1272, 2005. https://doi.org/10.1016/j.automatica.2005.02.002
20. H. Liang, and B. Wang, “Identification of MIMO Hammerstein Models Using Support Vector Machine” In International Symposium on Neural Networks, Springer,
    Berlin, Heidelberg, 2007. https://doi.org/10.1007/978-3-540-72395-0-51
21. Y. M. Hlaing, M. S. Chiu, and S. Lakshminarayanan “Modeling and control of multivariable process using generalized Hammerstein model” Chemical Engineering Research and Design Transactions, 85(4), 445-454, 2007. https://doi.org/10.1205/cherd06210
22. F. Ding, and T. Chen, “Identification of Hammerstein nonlinear ARMAX system” IEEE Transactions Automatic Control, 41(9), 1479-1489, 2005. https://doi.org/10.1016/j.automatica.2005.03.026
23. K. H.Chan, J. Bao, and W. J. Whiten, “Identification of MIMO Hammerstein systems using cardinal spline functions” Journal of Process Control, 16(7), 659–670, 2006. https://doi.org/10.1016/j.jprocont.2006.01.004 http://dx.doi.org/10.1080/00207721.2014.951419

(Click to view)

(Click to view)

No. of Downloads Per Month

No. of Downloads Per Country