Nonlinear parabolic problem with lower order terms in Musielak-Orlicz spaces

Volume 2, Issue 5, Page No 109-123, 2017

Author’s Name: Mhamed Elmassoudi^1,a), Ahmed Aberqi², Jaouad Bennouna¹

View Affiliations

¹University of Fez, Faculty of Sciences Dhar El Mahraz, Department of Mathematics, B.P 1796 Atlas Fez, Morocco.
²University of Fez, National School of Applied Sciences Fez,Morocco.

^a)Author to whom correspondence should be addressed. E-mail: elmassoudi09@gmail.com

Adv. Sci. Technol. Eng. Syst. J. 2(5), 109-123 (2017); DOI: 10.25046/aj020518

Keywords: Musielak-Orlicz space Nonlinear, Parabolic Problems, Entropy solution, Condition sign, Lower order term

Download Now!

422 Downloads

Export Citations

Abstract

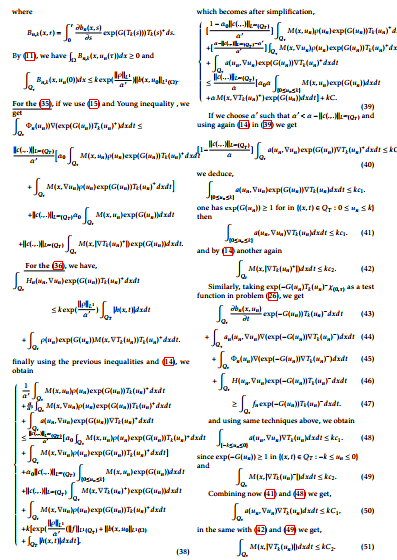
We prove an existence result of entropy solutions for the nonlinear parabolic problems: $\frac{\partial b(x,u)}{\partial t} + A(u) - div(\Phi(x,t,u))+H(x,t,u,\nabla u) =f,$ and $A(u)=-div(a(x,t,u,\nabla u))$ is a Leary-Lions operator defined on the inhomogeneous Musielak-Orlicz space, the term $\Phi(x,t,u)$ is a Cratheodory function assumed to be continuous on u and satisfy only the growth condition $\Phi(x,t,u)\leq c(x,t)\overline{M}^{-1}M(x,\alpha_{0}u)$ , prescribed by Musielak-Orlicz functions $M$ and $\overline{M}$ which inhomogeneous and not satisfy $\Delta_2$ -condition, $H(x,t,u,\nabla u)$ is a Cratheodory function not satisfies neither the sign condition or coercivity and $f\in L^{1}(Q_T)$ .

Received: 05 May 2017, Accepted: 15 July 2017, Published Online: 28 December 2017

Full Text

References (23)

M. Porzio, “ Existence of solutions for some noncoercive parabolic equations.”, Discrete and Continuous Dynamical Systems. 5.3, 553-568, 1999.
Boccardo, L. Orsina, A. Porretta, “ Some noncoercive parabolic equations with a lower order terms in divergence form.”, Journal of Evolution Equations 3.3 Dedicated to philippe B´enilan, 407-418,2003.
Di Nardo, F. Feo, O. Guib´e, “ Existence result for nonlinear parabolic equations with lower order terms.”, Analysis and Applications, Vol. 9, No. 2, 161186, 2011.
Aberqi, J. Bennouna, M. Mekkour, H. Redwane, “ Nonlinear parabolic inequality with lower order terms.”, Applicable Analysis 2016.
Boccardo, “ Dirichlet problems with singular convection terms and applications.”, Journal of Differential Equations 258 , 2290-2314,2015.
Boccardo, G. R. Cirmi, “ W1;1 0 solutions of some unilateral problems.”, Nonlinear Analysis Series A: Theorie, Methods and Applications, 121 , 447-457, 2015.
Zecca, “Existence and uniqueness for nonlinear elliptic equations with lower order terms.”, Nonlinear Analysis Serie A: Theorie, Methos and Applications, 75, 899-912, 2012.
Akdim, J. Bennouna, M. Mekkour, H. Redwane, “ Strongly nonlinear parabolic inequality in Orlicz spaces via a sequence of penalized equations.”, African Mathematical Union 2014.
Mabdaoui, H. Moussa, M. Rhoudaf, “ Entropy solutions for a nonlinear parabolic problems with lower order term in Orlicz spaces.”,Analysis and Mathematical Physics DOI 10.1007/s13324-016-0129-5, 2016.
Musielak, “ Modular spaces and Orlicz spaces.”, Lecture Notes in Math, 1983.
Ahmed, A. Benkirane, M.S.B.Elemine Vall, A. Touzani, “ Existence of entropy solutions for nonlinear elliptic equations in Musielak framework with L1 ”, Boletim da Sociedade Paranaense de Matematica (3s.) v. 36 1 : 125150, 2018.
Benkirane, M. Sidi El Vally, “ Some approximation properties in Musielak-Orlicz-Sobolev spaces.” , Thai Journal of Mathematics, pp. 371-381, 2012.
Benkirane, M. Sidi El Vally, “ Variational inequalities in Musielak-Orlicz-Sobolev spaces.” , Bulletin of the Belgian Mathematical Society, pp. 787-811, 2014.
L. Ahmed Oubeid , A. Benkirane, M. Sidi El Vally, “ Strongly nonlinear parabolic problems in Musiealak-Orlicz- Sobolev spaces.”, Boletim da Sociedade Paranaense de Matematica, v. (33) 1 , 193-225,2015.
Ait Kellou, A. Benkirane, S.M. Douiri, “ An inequality of type Poincare in Musielak spaces and applications to some nonlinear elliptic problems with L1-data.” ,Complex Variables and Elliptic Equations 60, pp. 1217-1242, 2015.
Redwane, “ Existence of a solution for a class of nonlinear parabolic systems. ”, Electronic Journal of Qualitative Theory of Differential Equations 24, 18pp., 2007.
Benkirane, J. Bennouna, “ Existence of entropy solutions for some nonlinear problems in orlicz spaces.”, Nonlinear Analysis 54, 85-102, 2001.
Adams, “ Sobolev spaces.”,New York (NY):Academic Press, 1975.
Brezis, “ Analyse fonctionnelle.”, Masson, 1987.
Landes, “ On the existence of weak solutions for quasilinear parabolic initial-boundary value problems.”, Proceedings of the Royal Society of Edinburgh Section A 89, 217-237, 1981.
Akdim, N. El gorch, M. Mekkour, “ Existence of renormalized solutions for p(x)-parabolic equations with three unbounded non- linearities.”, Boletim da Sociedade Paranaense de Matematica, v (3) 34 , no. 1, 225-252, 2016.
Blanchard, H. Redwane, “ Renormalized solutions for class of nonlinear evolution problems.”, Journal de Mathmatiques Pures et Appliques. 77, pp. 117-151, 1998.
S.B. Elemine Vall, A. Ahmed, A. Touzani, A. Benkirane, “ Existence of entropy solutions for nonlinear elliptic equations in Musielak framework with L1 data.”, Boletim da Sociedade Paranaense de Matematica, v (3s.) v. 36 1, 125150, 2018.

Nonlinear parabolic problem with lower order terms in Musielak-Orlicz spaces