Degenerate 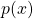 -elliptic equation with second membre in
-elliptic equation with second membre in 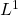
Volume 2, Issue 5, Page No 45-54, 2017
Author’s Name: Adil Abbassi1,a), Elhoussine Azroul2, Abdelkrim Barbara2
View Affiliations
1Sultan Moulay Slimane University, Mathematics, LMACS Laboratory, FST, Beni-Mellal, Morocco
2Sidi Mohamed Ben Abdellah University, Mathematics, LAMA Laboratory, FSDM, Fez, Morocco
a)Author to whom correspondence should be addressed. E-mail: abbassi91@yahoo.fr
Adv. Sci. Technol. Eng. Syst. J. 2(5), 45-54 (2017); ![]() DOI: 10.25046/aj020509
DOI: 10.25046/aj020509
Keywords: Sobolev spaces with weight and to variable exponents Truncations
Export Citations
In this paper, we prove the existence of a solution of the strongly nonlinear degenerate ![]() -elliptic equation of type:
-elliptic equation of type:
![]()
where ![]() is a bounded open subset of
is a bounded open subset of ![]() is a Caratheodory function from
is a Caratheodory function from ![]() into
into ![]() , who satisfies assumptions of growth, ellipticity and strict monotonicity. The nonlinear term
, who satisfies assumptions of growth, ellipticity and strict monotonicity. The nonlinear term ![]() checks assumptions of growth, sign condition and coercivity condition, while the right hand side
checks assumptions of growth, sign condition and coercivity condition, while the right hand side ![]() belongs to
belongs to ![]() .
.
Received: 12 April 2017, Accepted: 04 May 2017, Published Online: 10 December 2017
1 Introduction
Let Ω be a bounded open subset of IRN , N ≥ 2, let ∂Ω
its boundary and p(x) ∈ C(Ω) with p(x) > 1. Let ν be a weight function in Ω, ie: ν measurable and strictly positive a.e. in Ω. We suppose furthermore, that the weight function satisfies also the integrability conditions defined in section 2.
Let us consider the following degenerate p(x)-elliptic
| problem with boundary condition | |
| P)( Au +g(x,u,∇u) = f
( u = 0 |
in Ω,
on ∂Ω, |
where A is a Leray-Lions operator defined from
1,p(x) −1,p0(x)(Ω,ν∗) , with ν∗ =
W0 (Ω,ν) to its dual W
0
ν1−p (x), by :
Au = −diva(x,u,∇u).
where a is a Caratheodory function from´ Ω × IR × IRN −→ IRN who satisfies assumptions of growth, ellipticity and strict monotonicity, while the nonlinear term g: Ω×IR×IRN −→ IR checks assumptions of sign and growth. We suppose moreover that g checks the following condition of coercivity:
( ∃ ρ1 > 0,∃ ρ2 > 0 such that : for |s| ≥ ρ1, |g(x,s,ξ)| ≥ ρ2ν(x)|ξ|p(x)
We suppose also that the second member f belongs to L1(Ω).
Let consider the following degenerate p(x)-elliptic
| problem of Dirichlet: | ||
| ( Au +g(x,u,∇u) | = f | 0
in D (Ω), |
(1)
u, g(x,u,∇u) ∈ L1(Ω).
In the case where p is constant and without weight, there is a wide literature in which one can find existence results for problem (1). When the second member f belongs to W −1,p0 (Ω), A. Bensoussan, L. Boccardo and F. Murat [6] studied the problem and give an existence result. While if f ∈ L1(Ω) the initiated basic works were given by H. Brezis and Strauss [9], L. Boccardo and T. Galloue¨t [7] also proved an existence result for (1), which was extended to the a unilateral case studied by A. Benkirane and A. Elmahi [5]. When g is not necessarily the null function, T. Del Vecchio [10] proved first existence result for problem (1) in the case where g does not depend on the gradient and then in V. M Monetti and L. Randazzo [16] using, in both works, the rearrangement techniques. Whoever in [1], Y. Akdim, E. Azroul and A. Benkirane treated the problem (1) within the framework
1,p of Sobolev spaces with weight W0 (Ω,ω), but while keeping p constant.
- Azroul, A. Barbara and H. Hjiej [2] studied (1) , in the nonclassical case by considering nonstandard
1,p(x)
Sobolev spaces without weight W0 (Ω). See as well [3] where existence and regularity of entropy solutions was obtained for equation (1) with degenerated
second member.
Our objectif, in this paper, is to study equation (1) by adopting Sobolev spaces with weight ν(x), and
1,p(x) to variable exponents p(x), W0 (Ω,ν). We prove that the problem (1) admits at least a solution u ∈
1,p(x)
- Y. Akdim, E. Azroul and A. Benkirane, “Existence of solution for quasilinear degenerated elliptic equation.”, Electronic J. Equ. 71, 1-19, 2001.
- E. Azroul, A. Barbara and H. Hjiej, “Strongly nonlinear p(x)- elliptic problems with second member L1-dual.”, African Diaspora Journal of Mathematics. 16, Number 2, 11722, 2014.
- E. Azroul, H. Hjiej and A. Touzani, “Existence and regularity of entropy solutions for strongly nonlinear p(x)-elliptic equations.”, Electronic journal of differential equations. 68, 1-27, 2013.
- M. B. Benboubker, E. Azroul, A. Barbara, “Quasilinear Elliptic Problems with non standard growth.”, EJDE, 62, 1-16, 2011.
- A. Benkirane and A. Elmahi, “Strongly nonlinear elliptic unilateral problems having natural growth terms and L1 data.”, Rendiconti di matematica, Serie VII, 18, 28917303, 1998.
- A. Bensoussan, L. Boccardo and F. Murat, “On a nonlinear partial differential equation having natural growth terms and unbounded solution.”, Ann. Inst. Henri Poincar´e, 4, 347-364, 1988.
- L. Boccardo and T. Gallou¨ et, “Strongly nonlinear elliptic equations having natural growth terms and L1.”, Nonlinear Analysis Theory methods and applications, 19(6), 573-579, 1992.
- L. Boccardo and T. Gallou¨ et, “Nonlinear elliptic equations with right hand side measures.”, Comm. P.D.E., 17, 641-655, 1992 .
- H. Brezis and W. Strauss, “Semilinear second-order elliptic equations in L1.”, J. Math. Soc. Japan, 25(4), 565-590, 1973.
- 10. T. Del Vecchio, “Nonlinear elliptic equations with measure data.”, Potential Analysis, 4, 185-203, 1995.
- P. Drabek, A. Kufner and V. Mustonen, “Pseudomonotonicity and degenerated or singular elliptic operators.”, Bull. Austral. Math. Soc., 58, 213-221, 1998.
- X. L. Fan and Q. H. Zhang, “Existence for p(x)-Laplacien Direchlet problem.”, Nonlinear Analysis, 52, 1843-1852, 2003.
- X. L. Fan and D. Zhao, “On the generalized Orlicz-Sobolev Space Wk;p(x)().”, J. Gansu Educ. College, 12(1), 1-6, 1998.
- O. Kov´acik and J. R´akosnik, “On Spaces Lp(x) and Wk;p(x).”, Czechoslovak Math. J. , 41, 592-618, 1991.
- J. L. Lions, “Quelquesm´ethodes de r´esolution des probl`emes aux limites non lin´eaires.”, Dunod, 1969.
- V. M. Monetti and L. Randazzo, “Existence results for nonlinear elliptic equations with p-growth in the gradient.”, Riceeche di Matimaica, XLIX(1), 163-181, 2000.
- D. Zhao, X. J. Qiang and X. L. Fan, “On generalized Orlicz Spaces Lp(x)().”, J. Gansu Sci., 9(2), 1-7, 1997.
Citations by Dimensions
Citations by PlumX
Google Scholar
Scopus
Crossref Citations
- Elhoussine Azroul, Athmane Boumazourh, Mohammed Srati, "On positive weak solutions for a class of weighted (p(.), q(.))−Laplacian systems." Moroccan Journal of Pure and Applied Analysis, vol. 5, no. 2, pp. 125, 2019.
- Ghizlane Zineddaine, Abdelaziz Sabiry, Said Melliani, Abderrazak Kassidi, "Anisotropic obstacle Neumann problems in weighted Sobolev spaces and variable exponent." Journal of Applied Analysis, vol. , no. , pp. , 2024.
- Deepak Kumar Mahanta, "Existence and multiplicity of solutions for a class of quasilinear anisotropic elliptic systems via fibering method." The Journal of Analysis, vol. , no. , pp. , 2025.
- Adil Abbassi, Chakir Allalou, Abderrazak Kassidi, "Existence of Entropy Solutions for Anisotropic Elliptic Nonlinear Problem in Weighted Sobolev Space." In Nonlinear Analysis: Problems, Applications and Computational Methods, Publisher, Location, 2021.
- Elhoussine Azroul, Athmane Boumazourh, "A Sub-supersolutions Method for a Class of Weighted (p(.), q(.))-Laplacian Systems." In Recent Advances in Modeling, Analysis and Systems Control: Theoretical Aspects and Applications, Publisher, Location, 2020.
- Adil Abbassi, Chakir Allalou, Abderrazak Kassidi, "Existence of entropy solutions of the anisotropic elliptic nonlinear problem with measure data in weighted Sobolev space." Boletim da Sociedade Paranaense de Matemática, vol. 40, no. , pp. 1, 2022.
- Ghizlane Zineddaine, Abdelaziz Sabiry, Said Melliani, Abderrazak Kassidi, "Anisotropic obstacle Neumann problems in weighted Sobolev spaces with Hardy potential and variable exponent." SeMA Journal, vol. 82, no. 1, pp. 45, 2025.
- Soukaina Yacini, Adil Abbassi, Chakir Allalou, Abderrazak Kassidi, "On a Nonlinear Equation p(x)-Elliptic Problem of Neumann Type by Topological Degree Method." In Recent Advances in Fuzzy Sets Theory, Fractional Calculus, Dynamic Systems and Optimization, Publisher, Location, 2023.
- Adil Abbassi, Chakir Allalou, Abderrazak Kassidi, "Topological degree methods for a Neumann problem governed by nonlinear elliptic equation." Moroccan Journal of Pure and Applied Analysis, vol. 6, no. 2, pp. 231, 2020.
No. of Downloads Per Month
No. of Downloads Per Country









