1            Introduction

The optimization of state of charge for Lithium batteries presents the main effect on their internal states in several applications [1]. It leads to maintain the activities of applications in permanent way.

The state of charge (SoC) is meaningful parameter that is defined in case of discharge of the battery [2]. It presents the shift time of battery capacity through the following expression [3]:

Z t I^b(τ)

SoC(t) = 100^∗       dτ        (1) t0            Q

with I_b: the current of the battery, Q: the nominal capacity of the battery and τ: Time of energy storage. The SoC optimization is a difficult issue for different domains due to its dependency on some factors such as battery capacitance, temperature and internal resistance and also the problem of defining it easily [4]. Therefore, many researches have focused on the possibility to estimate the SoC of the Lithium cells through different techniques [5,6,7] such as Direct measurements [8], Book keeping estimation [9], SoC estimation based on models [10].

The most considered technique for SoC optimization is Observer techniques [11,12].

This method is based on puting the following battery model to the observer and update the optimization of the states by calculating their erros which are the set of difference data between the measured and desired state [13]. The model based methods presents among the diagnosis technology and especially fault diagnosis. They are designed for extraction parameter from impedance spectra and optimization the state of the electrochemical systems. It has been described in figure 1.

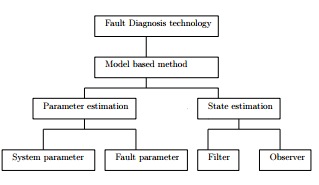Figure 1: Properties of the model based method for fault mechanism and diagnosis

The equivalent battery models permit to make conformity between electrochemical impedance and electric impedance measured by Electrochemical Impedance Spectroscopy (EIS). They own medium mathematical complexity and they ensure good precision in field of optimization.

In general, there is a fractional order aspect of equivalent models for electrochemical systems [14, 15,

16]. Moreover, the fractional models have been well defined by Fractional Order Calculus (FOC) [17]. Thanks to fractional order calculus, the several dynamic and chemical phenomena of Lithium battery have been perfectly characterized. Many researches have improved the efficiency of fractional order in electrochemical fields [18] for example: according to Ichise et al., fractional calculus has been used for analysis of electrode processes through an analog simulation of non-integer order transfer functions [19]. SoC estimation based on model for electrochemical systems requires an accurate fractional descriptor observers [20]. In addition, there are some researchers who have focused on this direction like Yan Ma and Xiuwen Zhou have considered the fractional kalman filter observer to optimize the state of charge of Li Ion batteries [21] and also Fei Zhang et al. has proposed the extended Kalman filter to ensure the stability of error estimation of SoC [22].

The objective of this research work consists on presenting new strategy for SoC estimation based on observer for Lithium cells.

Kalman Filter has been proposed to determine correctly the state of Lithium batteries. It has been more explained and described in section 4.2 . Indeed, Kalman filter has been theoritically checked and there has been improved that it is efficient method in field of prediction of State of Charge (SoC).

2          Dynamic model for Lithium battery

The Lithium battery considered in this paper is Lithium cell LiFePO4, model (SP-LFP40AHA). This part has focused on defining the dynamic phenomenon of selected Lithium battery by analysis of Impedance spectroscopy data in each frequency range.

In fact, Impedance Spectroscopy (IS) has been the most considered strategy in field of estimation of state of charge of electrochemical systems thanks to its benefits. It is direct measurement that precises a suitable circuit related to characteristics of impedance curve at the level of frequency domain [23]. The measurement of impedance has been carried out in frequency range from 0.01 Hz to 1 KHz. Futhermore, impedance spectroscopy may identify the parameters of the several components for the equivalent circuit such as diffusion coefficient and kinectic variables [24, 25, 26]. The Lithium battery is closely non linear system and there is difficulty to identify its chemical coefficients and variables. So, thanks to impedance spectroscopy, there is possibility to determine the several chemical internal reactions which then can be defined by equivalent model.

Figure 2 shows the measured impedance diagram in 50% of SoC for wide range of frequencies. The several dynamic phenomena of Lithium battery have been appeared in each frequency range.:

• Parasitic effects and electro migration in the electrolyte and connectors at high frequency part (300Hz < f < 355 Hz).
• Charge transfer inside the battery and exactly in the interface between the electrode and electrolyte at mid frequency part (354.8Hz < f < 3.54 Hz). It is identified by Z_CPE which is defined in next section.
• Diffusion phenomena of ionic species in low frequency (f < 3.54 Hz). It is identified by Z_w which is defined in next section.

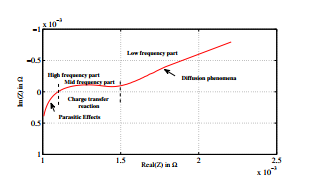Figure 2: Measured Impedance spectra for LiFePO4, model (SP-LFP40AHA) in 50% of SoC

Hence, the topology of equivalent model for chosen Lithium cell has been presented in figure 3. Dynamic battery has been modelled by set of electrical components.

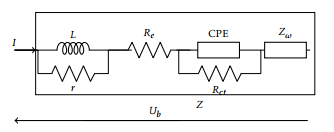Figure 3: Topology of equivalent model for Lithium cell LiFePO4, model (SP-LFP40AHA)

With I: the Current of LiFePO4 battery, Z: Impedance of LiFePO4 battery , U_b: the terminal of LiFePO4 battery.

The several effects over frequency range have been illustrated as:

• High frequency effects have been defined by inductance L in parallel with his interne resistance r .
• Electrode effects have been presented by ohmic resistance R_e.
• Mid frequency effects have been defined by parallel circuit constant phase element CPE- transfer resistance R_ct .
• Low frequency effects have been identified by Warburg impedance Z_ω

Li Ion cells is non linear electrochemical system and there is difficulty to deduce its appropriate properties. So, in order to obtain the optimal values of battery model variables which have been shown in figure

3, there has been used the genetic algorithm (G.A) as fitting procedure.

The optimal values of model have been determined through mechanism of evolutionnary algorithm which is described in figure 4.

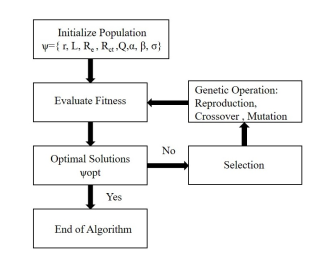Figure 4: Mechanism of Genetic Algorithm

The dynamic model for LiFePo4 has been described in figure 5 and its structure is based on hysterisis phenomenon which is presented by open circuit voltage OCV and from impedance spectroscopy analysis.

–

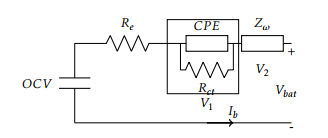Figure 5: Dynamic Model topology for Lithium cell

The inductance element L hasn’t been involved in the battery model because the Lithium ion cells are less applied in high frequencies range.

2.1         Parameters of battery model

There are different parameters related to equivalent model such as:

• The double layer capacitance CP E models the imperfect capacitors that appear in experimental spectra. It is defined by its fractionnary impedance through the following expression

[24]:

1

                                       ZCPE =  β                                        (2)

Q(jω)

with : Q > 0 , 0 ≤ β ≤ 1

• Z_ω is fractionnary impedance for warburg element. Its main characteristic consists in its straight line with constant slope at the level of Nyquist diagram in low frequency values. The impedance Z_ω can be written as in semi infinite diffusion [25]:

                                      Z                          (3)

with : α : the diffusion parameter and σ = 0.5 .

• OCV : Open Circuit Voltage and it is considered as crucial variable that expresses many criterias of performance for the battery. The open circuit voltage is used for SoC estimation [26].

A non linear relationship between OCV and SoC has been illustrated in the litterature. In fact, some recent works have proposed some approximations for this relationship in order to facilitate its calculation.

Among these approximations, the relation between OCV and SoC is considered as [27]:

                                                    1                        1

OCV (z) = K₀ +K

(4)

+K3 eλ3(z−1) +K4 eλ4z +K5z

with z is the state of charge of the battery, K_i=1…5 are the linear parameters and λ_i=1..4 , Θ_i=1..2 are the non linear parameters.

Table 1 presents each values of the following coefficient K_i in order to fit the measured curve OCV . This set of values has been determined by Genetic Algorithm and it has been considered as optimal results by the process.

Table 1: Values of coefficient K_i

K0	K1	K2	K3	K4	K5
2.67	2.7	2.85	2.93	3.1	3.4

This approximation relationship has been plotted in figure 6.

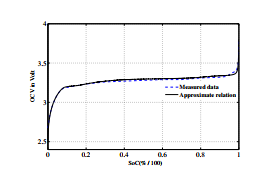Figure 6: Diagram of OCV over SoC range

The objectif of battery model is defining the several electrochemical reactions which own the fractional criterias. They are expressed by Fractional Order Calculus (FOC).

3          Non Linear fractional model

The dynamic model which has been shown in figure 5 is considered as non linear fractional model. The fractional order calculus is a tool for defining the fractional models. The fractional aspect in general presents among the characteristics of electrochemical systems. They have been developed and evaluated through fractional order calculus in some researches [28]. Besides, by recent works, the FOC has been defined as mathematic operator using differentiation with integration to non integer order aD_t^q where q: the order, a and t : the bounds of the operation. It is applied in science fields like bioengeneering [29], electronics [30, 31] and control theory [32]. In addition, almost engineer applications have focused on FOC startegies which are based generally on describing the aspects of dynamic systems by condensed expressions and considering non local characteristics such as thermal diffusion phenomenon [33] and botanical electrical impedances [34].

Fractional order calculus is denoted as [35]:

                                     dtdq^q                 if    q > 0

                        aDt^q = ^ 1                if    q = 1                       (5)

                                     ^ R0t dτ−q      if    q < 0

with aD_t^q is initialized q^th order differintegration.

At the level of this work, FOC is fractional differentiation and according to Grunwald-Leitnikov, it can be written as [36, 37]:

t

                 Dqx(t) = lim       1q X4T (−1)i qi!x(t −i4T )          (6)

4T →0 T

i=0

with 4T : the sampling time, q: the order GrunwaldLeitnikov fractional derivative of x(t).

                               q!                 Γ(q +1)

                                     =                         (7)

                                i           Γ(i +1)Γ(q −i +1)

where Γ(q) is the generalization of factorial function [38]. It is expressed as:

Z ∞

                                 Γ(q) =            y^q−1e^−ydy                             (8)

0

In this part, the constant phase element CP E and the warburg element Z_ω have been considered as fractional elements [39].

In fact, the fractional element is defined as [39]:

1

                                   Zf ractional ⁼   _δ                                          (9)

Y(jw)

where: Y is the coefficient; −1 ≤ δ ≤ 1 : the arbitrary order of the fractional element which can be an integer or a fraction. It is characterized by straight vertical line in Nyquist plot for low frequency domain.

For CP E, its fractional model is given as [20]:

1

                                       ZCpe =  β                                             (10)

C₁(jω)

For Z_ω, its fractional model is given as [20]:

1

                                   Zwarburg ⁼                _σ                                          (11)

W(jω)

where: W is the coefficient and β, σ are the arbitrary orders of the fractional elements: 0 ≤ σ ≤ 1 and 0 ≤ β ≤ 1.

In this work, the double layer capacitance CP E has treated as perfect capacitor C₁ and then its following equation is given as:

1

                                   ZCpe = C1(jω)                            (12)

Among the effectiveness of FOC for electrochemical systems, it defines precisely the chemical phenomenon of Lithium batteries. It has been improved in figure 7 for measured impedance spectrum in 50% of SoC of Lithium batteries.

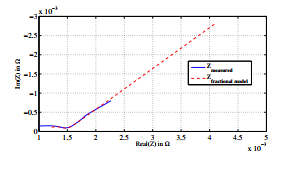Figure 7: Measured Impedance vs Impedance model presented by FOC

The dynamic behavior of the battery which has

been presented by FOC has been given as:

• For diffusion phenomenon: It has been defined by Z_warburg.
• For charge transfer phenomenon: It has been defined by capacitor C₁ in parallels with resistor R.

According to figure 7, the diffusion phenomena has been obvisiouly well defined by FOC. The straight line of Z_warburg is similar to line with constant slope of Z_ω.

Thanks to FOC, the equivalent circuit of the battery can be deduced and hence the chemical reactions can be identified through many parameters related to different circuit components.

3.1         Fractional battery model

The equations of the fractional model from figure 4 has been expressed as in the following form:

                                       DβV1 = Ib − V1                                                     (13)

                                                  C1           RctC1

where V₁: the voltage at the level of R_ctC₁ parallel circuit.

                                          Dσ V2 = Ib                                                    (14)

W

where V₂: the voltage at the level of warburg element.

                                           D¹z = ^Ib                                                      (15)

C_n

where C_n : the capacity of the Li Ion battery .

The voltage of Lithium battery V_bat is the sum of open voltage and voltages at the level of the electrode resistance R_e , the RC parallel circuit and warburg element.

It can be written as:

                             V_bat = OCV (z)+R_eI_b +V₁ +V₂                                  (16)

3.2         State space for Lithium battery model

Through the different equations (13)-(16), the state space for Lithium cell can be given as:

D^qx(t) = Ax(t)+Bu(t)

(17)

y = Cx(t)+Du(t)

where: x(t): the vector of the following states;

x =z      V1         V2 T A, B, C, D: The matrices with:
                                 1  0 0 0 Cn   Rct−1C1 0 0 , B=C111 , C= K5 A=   0          0    0         W	1	1 ,
D= Re, q = 1 β σ , y= Vbat: Output of state space.

u(t): Input of state space with u=I_b (The current

of the battery).

4          SoC optimization using fractional observer

The observers have been considered as an alternating tool for some problems which exist in practice like: the high cost of installation of the devices and long time of measurements of the missing variables. The main role of observers is determining the unknown variables related to the state vector and reducing the use of expensive sensors [40]. This area has been attractive by many researches [41,42] and many kind of observer strategies have been evolved especially for several classes of chemical systems to estimate their internal states [43, 44]. In addition, the use of observers becomes a challenge in front of many requirements of accuracy and suitable estimation performances. For the recent workers, there was set of types of observers which have been cited in electrochemical fields [45].

The design of observers owns an appropriate methodolgy. It has been firstly based on linear forms with presence of noises [46]. Then, there has been a developpement at the level of their forms due to the complexity of the systems. Hence, non linear observers have been widely considered [47]. They have based on mathematical models and they are evaluated by observer’s equations. Indeed, the gain and the optimization of error dynamics are the main properties for model based observers.

Figure 8 presents the procedure of observer design.

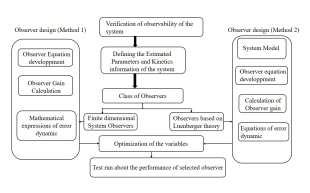Figure 8: Procedure of observer design

Moreover, the observer is among elements of control theory and it estimates in real time the state of given system from measurements of its inputs and outputs. Its principle has been described in figure 9.

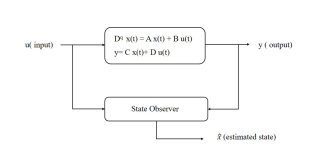Figure 9: Reconstruction of state space involving the state observer

4.1         Observability of non linear fractional model

The observability is criteria for control approach. It is based on defining the behavior of internal states of the system by knowledge of its measured outputs [48]. The observability condition is main part for observer designing and especially it depends on the formulation of the given system where there is choice of type of observability. Futhermore, there is two kinds of observability conditions: observability matrix and observability Gramian. In this work, the observability Gramian [49] has been considered to detect the aspect of given system.

The state space (17) for non linear fractional system has been firstly evaluated for its observability and then it has been put into the state observer. It is effectively observable at time t if there is θ < t where the state at time t can be finded by knowing its outputs over the interval [θ t] [50].

The observability Gramian matrix W(θ, t) is defined as [51]:

Z t

W(θ,t) =                               E_γ(A^T (t −τ)^γ)C^T CE_γ(A(t −τ)^γ)dτ (18)

θ

where E_γ is Mittag-Leffler function which is expressed as follows [52]:

                                                X∞            Ak

                                  E_γ(x) =                                   (19)

Γ(1+γk) k=0 with γ > 0

According to the battery model, the observability matrix W(θ, t) is expressed as:

 6.100  W(θ, t)= 5.75  5.9512

5.8965 5.9512 6.12

5.9512  6.110  7.110 

This matrix is invertible and thus its inverse W⁻¹(θ,t) exists.

Futhermore, the non linear fractional model is observable and there is possibility to estimate its internal state from knowledge of its external outputs. Hence, this model would be synthetized through an observer by following method which has been shown in figure 10 :

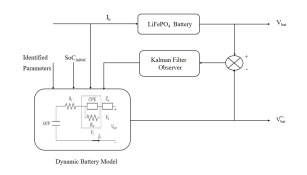Figure 10: Battery model based on SoC estimation through the feedback method Kalman filter observer

As described in figure 10, SoC estimation is ensured by feedback method Kalman Filter which has been explained in next sections.

4.2         Fractional Kalman filter (FKF) observer design

Model battery variables are not available directly to measure them. Hence, they need an accurate optimal tool to determine them which is fractional kalman filter (FKF).

Kalman filter is an estimator algorithm based on the informations about the given model and input, output signals in presence of noise [53]. Its operation can be done in real time using the actual input measurements and the previously calculated states. Kalman filter doesn’t need past informations during its run where it tries to find the minimum mean square error optimization states of the actual Lithium states.

The objectif of fractional Kalman filter is getting an appropriate optimization results by reducing the cost function in the following steps [54]: arg min[(xˆ_k −x)Pˆ_k⁻¹(xˆ_k −x)^T +(y_k +Cx)R_k⁻¹(y_k +Cx)^T ] x

(20)

with xˆ_k is the state vector prediction and Pˆ_k is the er-

ror covariance of state estimation.

The FKF is recursive algorithm and the form of state space (17) has been expressed as discrete form from stochastic theory:

For k ≥ 1 : x(k +1) = [4^qT A+diag(q)I]x(k)

                            N+1                   !

−^X(−1)^{i q} x(k +1−i)+4^qT Bu(k)

                                                i                                                 (21)

i=2

+w(k) y(k) = Cx(k)+Du(k)+v(k)

with qi! = γ = C i = i!(qq−!i)! i                  q

w(k): Stochastic disturbance; v(k): Output noise.

Fractional Kalman filter owns two main steps where the state estimate is evaluated through several equations presented in figure 11:

• Prediction step: permits to compute and update the state estimate and error covariance through mathematical relation between the priori estimation (xˆ_k⁻,Pˆ_k⁻) and the posterior estimation (xˆ_k⁺,Pˆ_k⁺).
• Correction step: updates the measurements of state estimate and error covariance.

The formulation of FKF designed for state optimization [20, 55, 56] has been summarized in figure 11:

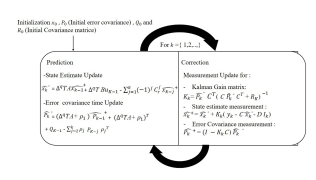Figure 11: Fractional Kalman Filter for state optimization

5          Simulation results and analysis

The performance of fractional Kalman filter has been evaluated for SoC estimation of the battery by Logiciel Matlab Simulink and the run time of simulation is about 1000 secondes.

The several simulation results have been performed through set of conditions:

• The fractional model of Lithium battery is observable
• The initial SoC value has been considered as

0.88.

• Presence of stochastic disturbance and output noise w(k) and v(k).

5.1         Analysis of error for SoC estimation

Figure 12 shows the SoC optimization by proposed observer Kalman filter and its error estimation.

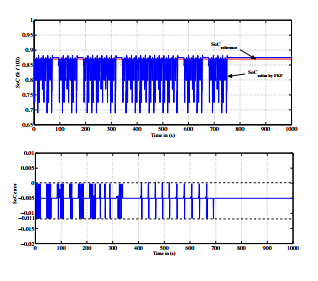Figure 12: SOC estimation and its error by Fractional Kalman filter observer

According to figure 11, Kalman filter well optimize the SoC of the battery . It provides good state of charge estimation error thanks to its accuracy for parameter estimation. Hence, the stability between the model and the observer has been perfectly ensured by Kalman filter.

Besides, the dispersion of error of SoC estimation for fractional kalman filter is not totally concentrated at zero error. It is more dispersed and tends to -0.005 due to the problem of choice of initial parameters. This explains that the optimal values of SoC are not exactly equal to real SoC values.

5.2         Analysis of rise time for SoC estimation

The rise time of proposed estimation method may explain about its speed responses and improves its dynamic performance.

The desired state of charge by Kalman filter observer converges slowly to real state. Thus, it isn’t considered for real time applications.

Kalman filter owns limits for convergence of the variables. It takes a long period to reach to real values of the following state of charge (SoC) due to its slowly operations. According to figure 11, the estimated state has been firstly fluctuated in narrow range and then it has been converged to real SoC. Hence, Kalman Filter observer is very slow method and it owns long rise time for SoC estimation.

So, Kalman filter doesn’t operate perfectly in term of estimation rise time and it yields to get bad quality of state optimization for electrochemical systems. It has high time consumption due to the long time of calculation of the covariances (P_k, Q_k, R_k).

5.3         Discussion

The dynamic performance of Kalman filter has been synthetized through simulation results. Kalman filter observer can estimate the state of charge of Lithium battery despite of its limits.

In fact, it has high time consumption which depends on two reasons:

• The first reason: It is related to calculation of feedback coefficients. For Kalman filter, its gain is determined through the equations related to prediction and correction steps.
• The second reason: There is long time of calculation of complex covariances which makeS a big time consumption for Kalman filter.

Besides, Kalman filter has high estimation rise time due to its slow responses for SoC prediction of

Lithium batteries.

In order to get better the state estimation for batteries, the extension form of these proposed techniques can be considered.

6          Conclusion and Outlook

A new strategy for SoC estimation has been described in this work which has based on state observer. Its main principle is using the equivalent fractional model of Lithium battery and determining from it the state of charge through observer methods. The battery model has been defined from impedance spectroscopy analysis. Each chemical property of the battery has been modelled through set of electrical components. The selected technique for state optimization is Fractional Kalman filter. Its operation for SoC estimation has been explained. The performance of this method and several aspects of SoC estimation (Rise time and time consumption) have been evaluated theoretically and there has been improved that Kalman filter observer has benefits and limits to predict the internal state of the batteries due to its long rise time and time consumption.

Future goals of this work is overcoming the limits of Kalman filter by considering its extension form or a robust and fast observer tool for SoC estimation which is Proportional Integral Observer (PIO). It well defines through its operations the actual states of electrochemical systems.

1. Garcia-Valle, Rodrigo, Peas Lopes, Joo A, Electric Vehicle Integration into Modern Power Networks, Springer Verlag New York 2013.
2. P. Christopher Manning, Eli White, Douglas Nelson, Abhijit Khare, Development of a Plug-In Hybrid Electric Vehicle Control Strategy Employing Software-In-the-Loop Techniques, SAE 2013 World Congress & Exhibition.
3. Akram Eddahech, Olivier Briat, Jean-Michel Vinassa, Realtime SOC and SOH estimation for EV Li-ion cell using online parameters identification, Energy Conversion Congress and Exposition (ECCE), 2012 IEEE.
4. John Chiasson, Baskar Vairamohan, Estimating the State of Charge of a Battery, IEEE transactions on control systems technology, vol. 13, no.3, May 2005.
5. Languang Lu, Xuebing Han, Jianqiu Li, Jianfeng Hua, Minggao Ouyang, A review on the key issues for lithium-ion battery management in electric vehicles, Journal of Power Sources: Volume 226, 15 March 2013, Pages 272 – 288.
6. Nalin A. Chaturvedi, Reinhardt Klein, Jake Christensen, Jasim Ahmed, Aleksandar Kojic, Algorithms for Advanced Battery-Management Systems, IEEE Control Systems (Volume: 30, Issue: 3, June 2010).
7. Nicolas Watrin, Benjamin Blunier, A.Miraoui, Review of adaptive systems for lithium batteries State-of-Charge and State-of-Health estimation, Transportation Electrification Conference and Expo (ITEC), 2012 IEEE.
8. Li Ran, Wu Junfeng, Wang Haiying, Li Gechen, Prediction of state of charge of Lithiumion rechargeable battery with electrochemical impedance spectroscopy theory, Industrial Electronics and Applications (ICIEA), 2010, the 5th IEEE Conference on.
9. Valer Pop , Henk Jan Bergveld, Dmitry Danilov, Paul P. L. Regtien, Peter H. L. Notten, Battery Management Systems: Accurate State-of-Charge Indication for Battery-Powered Applications, Springer Netherlands, Volume: 9, 2008.
10. Dorin V. Cadar, Dorin M. Petreu, Cristian A. Orian, A method of determining a lithium-ion battery’s state of charge, Design and Technology of Electronics Packages, (SIITME) 2009. 15th International Symposium for.
11. Kong Soon Ng, Chin-Sien Moo, Yi-Ping Chen, Yao-Ching Hsieh, Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries, Applied Energy, Volume 86, Issue 9, September 2009, Pages 1506 -1511.
12. Xiaosong Hu, Fengchun Sun, Fuzzy Clustering Based Multimodel Support Vector Regression State of Charge Estimator for Lithium-ion Battery of Electric Vehicle, Intelligent Human-Machine Systems and Cybernetics, 2009. IHMSC’ 09. International Conference on.
13. Valer Pop, Henk Jan Bergveld, Dmitry Danilov, Paul P. L. Regtien, Peter H. L. Notten, Battery Management Systems: State of-the-Art of battery, State-of-Charge determination, Springer Netherlands, pp 11-45, 2008.
14. Fengchun Sun, Xiaosong Hu, Yuan Zou, Siguang Li, Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles , Energy, Volume 36, Issue 5, May 2011, Pages 3531 – 3540.
15. Jonghoon Kim, B. H. Cho, State-of-Charge Estimation and State-of-Health Prediction of a Li-Ion Degraded Battery Based on an EKF Combined With a Per-Unit System , IEEE transactions on vehicular technology, vol. 60, no. 9, November 2011.
16. Bharath Pattipati, Chaitanya Sankavaram, Krishna Pattipati, System Identification and Estimation Framework for Pivotal Automotive Battery Management System Characteristics, IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), Volume: 41, Issue: 6, Nov. 2011.
17. Yulan Zhao, Haitao Yun, Shude Liu, Huirong Jiao, Chengzhen Wang, State-of-charge Estimation for Lithium-ion Batteries Using a Multi-state Closed-loop Observer, Journal of Power Electronics, Vol. 14, No. 5, pp.1038-1046, September 2014 .
18. Lokenath Debnath, Recent applications of fractional calculus to science and engineering, Journal of Power Electronics, Vol. 14, No. 5, pp.1038-1046, September 2014.
19. M.Ichise, Y.Nagayanagi and T.Kojima , An analog simulation of non-integer order transfer functions for analysis of electrode processes, Journal of Electroanalytical Chemistry and Interfacial Electrochemistry Volume 33, Issue 2, December 1971, Pages 253 -265.
20. Jun Xu, Chunting Chris Mi, Binggang Cao, Junyi Cao, A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model, Journal of Power Sources, Volume 233, 1 July 2013, Pages 277 – 284.
21. Yan Ma, Xiuwen Zhou, Bingsi Li and Hong Chen, Fractional modeling and SOC estimation of lithium-ion battery, IEEE/CAA Journal of Automatica Sinica, Volume: 3, Issue: 3, July 10 2016.
22. Fei Zhang, Guangjun Liu and Lijin Fang, A battery State of Charge estimation method with extended Kalman filter, Advanced Intelligent Mechatronics, AIM 2008. IEEE/ASME International Conference on.
23. S.M.M. Alavi, C.R. Birkl, D.A. Howey, Time-domain fitting of battery electrochemical impedance models, Journal of Power Sources, Volume 288, 15 August 2015, Pages 345352.
24. Baojin Wang, Zhiyuan Liu, Shengbo Eben Li, Huei Peng,State-of-Charge Estimation for Lithium-Ion Batteries Based on a Nonlinear Fractional Model, IEEE Transactions on Control Systems Technology, May 2016.
25. Dominik Sierociuk, ANDRZEJ DZIELINSKI, Fractional Kalman Filter algorithm for the states, parameters and order of fractional system estimation, Int. J. Appl. Math. Comput. Sci., 2006, Vol. 16, No. 1, 129 -140.
26. Tarek Raissi, Mohamed Aoun, Robust state estimation for fractional systems, Conservatoire National des Arts et Metiers – Paris, France, National Engineering School of Gabes, Tunisia, Rome, September 14 – 16, 2016.
27. J.C. Trigeassou, N. Maamri, J. Sabatier, A. Oustaloup, A Lyapunov approach to the stability of fractional differential equations, Signal Processing Volume 91, Issue 3, March 2011, Pages 437 – 445.
28. S. Buller, M. Thele, R.W.A.A. De Doncker, E. Karden, Impedance-based simulation models of supercapacitors and Li-ion batteries for power electronic applications, IEEE Transactions on Industry Applications, Volume: 41, Issue: 3, May-June 2005.
29. Autolab Application Note EIS04, Electrochemical Impedance Spectroscopy (EIS) Part 4 Equivalent Circuit Models, 1 July 2011.
30. Li Ran, Wu Junfeng, Wang Haiying, Li Gechen, Prediction of state of charge of Lithium-ion rechargeable battery with electrochemical impedance spectroscopy theory, Industrial Electronics and Applications (ICIEA), 2010, the 5th IEEE Conference on.
31. Domenico Di Domenico, Yann Creff, Eric Prada, Pascal Duchene, Julien Bernard, Valrie Sauvant-Moynot, A Review of Approaches for the Design of Li-Ion BMS Estimation Functions, Oil & Gas Science and Technology Rev. IFP Energies nouvelles, Vol. 68 (2013), No. 1, pp. 127-135.
32. J.-P. Diard, B. Le Gorrec, C. Montella, ELECTRICAL CIRCUITS CONTAINING CPEs, Bio-Logic, March 29, 2013.
33. J.-P. Diard, B. Le Gorrec, C. Montella, DIFFUSION IMPEDANCES, Bio-Logic, August 7, 2012.
34. JLei Pei, Rengui Lu, Chunbo Zhu, Relaxation model of the open-circuit voltage for state-of-charge estimation in lithium-ion batteries, IET Electrical Systems in Transportation Volume: 3, Issue: 4, December 2013.
35. Fei Feng, Rengui Lu , Guo Wei, Chunbo Zhu, Online Estimation of Model Parameters and State of Charge of LiFePO4 Batteries Using a Novel Open-Circuit Voltage at Various Ambient Temperatures, Energies, April 2015.
36. I. Sadli, M. Urbain, M. Hinaje, J.-P. Martin, S. Ral, and B. Davat, Online Estimation of Model Parameters and State of Charge of LiFePO4 Batteries Using a Novel Open-Circuit Voltage at Various Ambient Temperatures, Energy Conversion and Management 51, 2010, 2993-2999.
37. Laurent Sommacal ,Pierre Melchior, Jean-Marie Cabelguen, Alain Oustaloup, Auke Jan Ijspeert, FRACTIONAL MULTIMODELS OF THE GASTROCNEMIUS FROG MUSCLE, IFAC Proceedings Volumes, Volume 39, Issue 11, January 2006, Pages 254-259.
38. B. T. Krishna, K. V. V. S. Reddy, Active and Passive Realization of Fractance Device of Order 1/2, Hindawi Publishing Corporation Active and Passive Electronic Components Volume 2008, Article ID 369421, 5 pages.
39. Yifei Pu, Xiao Yuan, Ke Liao, Jiliu Zhou, Ni Zhang, Xiaoxian Pu, Yi Zeng, A recursive two-circuits series analog fractance circuit for any order fractional calculus, ICO20: Optical Information Processing, China, August 21, 2005.
40. Gary W. Bohannan, Analog Fractional Order Controller in Temperature and Motor Control Applications, Journal of Vibration and Control 14(9-10):1487-1498, September 2008.
41. J.-D. Gabano, T. Poinot, Fractional modelling and identification of thermal systems, Signal Processing Volume 91, Issue 3, March 2011, Pages 531 – 541.
42. Isabel S. Jesus, J.A. Tenreiro Machado, J. Boaventura Cunha, FRACTIONAL ELECTRICAL DYNAMICS IN FRUITS AND VEGETABLES, IFAC Proceedings Volumes, Volume 39, Issue 11, January 2006, Pages 308-313.
43. Ivo Petras, YangQuan Chen, Fractional-order circuit elements with memory, Carpathian Control Conference (ICCC),2012, 13th International.
44. Ivo Petras, Fractional-Order Nonlinear Systems Modeling, Analysis and Simulation, ISBN 978-3-642-18100-9, Springer Heidelberg Dordrecht London New York, 2011.
45. Concepcin A. Monje, YangQuan Chen, Blas M. Vinagre, Dingy Xue, Vicente Feliu, Fractional-order Systems and Controls Fundamentals and Applications, ISBN: 978-1-84996-334-3, Book Advances in Industrial Control 2010.
46. Dochain D, Couenne F, Jallut C, Enthalpy based modelling and design of asymptoticobservers for chemical reactors, “International Journal of Control” – Vol. 82, no. 8, p. 1389-1403 (2009).
47. Aguilar-Garnica E, Garcia-Sandoval JP, Gonzalez-Figueredo C, A robust monitoring tool for distributed parameter plug flow reactors, Computers & Chemical Engineering Volume 35, Issue 3, 8 March 2011, Pages 510-518.
48. Lpez-Negrete R, Biegler LT, A moving horizon estimator for processes with multi-rate measurements: a nonlinear programming sensitivity approach, Journal of Process Control Volume 22, Issue 4, April 2012, Pages 677-688.
49. del-Muro-Cuellar B, Velasco-Villa M, Jimnez-Ramrez O, Fernndez-Anaya G, lvarez-Ramrez J, Observer-based smith prediction scheme for unstable plus time delay processes, Ind. Eng. Chem. Res. 2007, 46, 4906-4913.
50. B.S. Bhangu, P. Bentley, D.A. Stone, C.M. Bingham, Observer techniques for estimating the state-of-charge and state-of-health of VRLABs for hybrid electric vehicles, Vehicle Power and Propulsion, 2005, IEEE Conference.
51. Kravaris C, Hahn J, Chu Y, Advances and selected recent developments in state and parameter estimation, Computers & Chemical Engineering, Volume 51, 5 April 2013, Pages 111-123.
52. K. Balachandran, V. Govindaraj, M. Rivero, J. A. Tenreiro Machado and J. J. Trujillo , Observability of Nonlinear Fractional Dynamical Systems, Hindawi Publishing Corporation Abstract and Applied Analysis, Volume 2013, Article ID 346041, 7 pages.
53. Lee S, Observer for discrete-time Lipschitz non-linear systems with delayed output, IET Control Theory & Applications, Volume: 5, Issue: 1, January 6, 2011.
54. Dong Y, Yang Y, Observer design for a class of multi-input multi-output nonlinear systems, International Journal of Systems Science Volume 42, 2011 – Issue 4.
55. Katsuhiko Ogata, Modern Control Engineering Fifth Edition, ISBN-13: 978-0136156734, Pearson, September 4, 2009.
56. Tsakalis K, Stability, controllability and observability, 2013.

(Click to view)

(Click to view)

No. of Downloads Per Month

No. of Downloads Per Country