1. Introduction

Recent years, power system stability and reliability have been take into account as very important issues in the context of modern power system [1]. Stressed operating conditions and competitive business enjoinments have been showing threats to power engineers for an efficient design and optimal utilization of the electrical utilities. In earlier day’s system stability issue were classified as the problem related with transient stability, but, the small oscillations of magnitude 0.2-2 Hz were not major consideration. To ensure transient stability fast acting Automatic Voltage Regulators (AVRs) were employed with generators. However, later in 1960 Concordia et.al., discovered that these high gain regulators are main culprit for introducing the negative damping in the system [2].

The under damped system has an oscillatory response; hence it inculcates oscillatory instability in the power system. The oscillations of small magnitude are harmful for the stability of a power system. These oscillations can cause system collapse if not handled accurately [3]. To find a potential and cost-effective solution to this issue, initial work on Power System Stabilizer (PSS) was proposed by E. V. Larsen et.al. The AVR and PSS are dynamically interlinked instruments; one increases transient stability and other complement the small signal stability. To augment the system stability, design engineers should keep a bird eye’s view on electromagnetic torque of the generator [4]. It has two elements; synchronizing torque, it is in phase with the variation in angle δ (load angle) and other is damping torque, which is in phase with speed deviation [5].

Design of damping controller for a poorly damped system is a formidable problem for power engineers. The damping controller is not only a potential answer for the oscillatory instability but also provides a good damping over the variety of operating conditions. The design of PSS has an ample significance to ensure the oscillatory stability. The Conventional Power System Stabilizer (CPSS) is a lead lag compensator [6]. For designing the damping controller, a designer has to find an accurate set of parameters (Gain & time constant).Proper tuning of the Lead Lag loop presents an adequate amount of damping to the system which helps the system to overcome with oscillatory instability [7].

Over the last decade many techniques were reported by the scientists to solve the PSS factor estimation problem. Some of these researches introduced techniques, to gain the robust conventional design through optimization, adaptive design with the help of expert systems (Neural Network, Fuzzy and Hybrid system), Linear Matrix Inequalities (LMI), Pole Placement and many others [8].

Recent years the enhancement in the field of damping controller design is revolutionized by the Evolutionary Algorithms. Evolutionary computations came in the picture in early 80’s. Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Biography Based Optimization (BBO), Bacterial Foraging Algorithm (BFA) and many more were proposed. These procedures are mathematical adaption of nature. They use nature rules to find the global optimum answer. PSS parameter estimation is a complex optimization issue [9].

The procedure towards the designing of CPSS contains following steps [10]:

1. Stability of any system depends on its initial operating conditions. In order to obtain the robust design hard operating conditions should be studied.
2. The design of the PSS should be investigated over various types of perturbations, fault locations and dissimilar system configurations. These contingencies help to ensure that design gained from the approach is robust enough [11].
3. Eigen Property analysis should be done to validate the efficacy of the design.

2.       Small Signal Stability

Stability problems have already acquired prominence with every passing day. The need of the hour is to develop a robust system, which is not likely to give up in the wake of blackouts and various contingencies. IEEE/CIGRE Joint Task Force committee introduce the power system stability as follows “Small-disturbance (or small-signal) rotor angle stability is concerned with the ability of the power system to maintain synchronism under small disturbances. The disturbances are considered to be sufficiently small that linearization of system equations is permissible for purposes of analysis” [12].

Power system utilities still prefer the conventional lead-lag power system stabilizer structure.  Since the PSS has engrossed the interest of researchers, extensive research has been conducted in the following fields:

• Effect of PSS on system stability
• PSS tuning methods
• Practical experience in design, installation & operation of PSS.

Figure 1 shows the conventional Delta-Omega PSS. A stabilizer is designed by suitable selection of time constants T_ω, T₁, T₂, T₃, T₄ and stabilizer gain K_STAB. In practical situation, a torsional filter is used for attenuating the stabilizer gain at turbine generator shaft torsional frequencies and may be neglected while designing PSS [13].

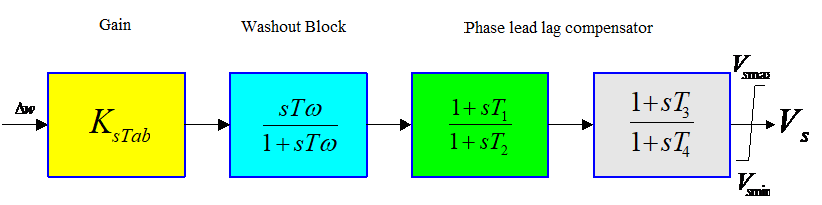Figure 1. Power System Stabilizer transfer function model

Where K_S is Stabilizer gain, T_ω is Washout time constant and T₁, T₂, T₃, T₄ are time constants of the lag lead networks [14].

The problem first encountered in the year 1969 reported by Concordia et al. was negative damping injection by turbine’s speed governor loop. It could be resolved by fitting the generators with a feedback controller. This controller sensed the change in terminal power of the generator and fed it back at the AVR reference input with proper phase lead and magnitude. This generated an additional damping torque on the rotor. Hence this fact advocates the acute requirement of PSS for adequate damping in the modern power networks. Larsen and Swann [15] in 1981discussed the chronological development of damping controllers in their three-part paper. They recommended that the objective of the most appropriate stabilizer tuning criterion is to provide an adequate amount of damping to local mode of oscillations and inter area modes of oscillations. Michael J. Basler et al. [16] discussed power system instability and the importance of fast disturbance clearing performance. Explanation is provided regarding small signal stability, high impedance transmission lines, line loading, and high gain, fast acting excitation systems [17].

3.       The Swarm Intelligent Techniques Algorithm

Swarm intelligence is a research field that models the communal behavior in swarms of insects or animals. Several algorithms ascending from these models have been anticipated to solve an extensive range of complex optimization problems. In this work, comparative study of novel swarm algorithms like Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) will be considered to estimate the parameters of PSS [18].

3.1.  Particle Swarm Optimization

The particle swarm optimization (PSO) technique is a population based optimization technique first proposed by Kennedy and Eberhart in 1995 inspired by social behavior of bird flocking or fish schooling [19]. PSO as an optimization tool provides a population based search procedure in which individuals called particles change their position (state) with time [14]. In a PSO system particles fly around in a multidimensional search space; during their flight, each particle adjusts its position according to its own experience ( ) and according to its neighbor’s experience ( , making use of the best position encountered by itself and its neighbors.

The position of particle in an n dimensional vector can be represented mathematically as [20]:

The modification is made in current position using following equation [21]:

Where  represents the current position of the particle,  represents the modified position of the particle and  is the velocity of each particle [22].

The velocity of each particle is n-dimensional vector given by the following equation:

The velocity of each particle is updated after every iteration according to the following equation:

Where  is the current velocity of the particle,  is the modified velocity of the particle, is the pbest of particle i, is the gbest of particle i, m is the number of members in a particle,  is the weight function for velocity of particle i and  is the weighing coefficients for each particle [23].

The objective function will be taken as fitness function for PSO algorithm. The best position related to the lowest value of the objective function for each particle is given as [24]:

And global best among all particles or best out of all pbest is represented as:

The velocity and position of particles are updated after each iteration [25].

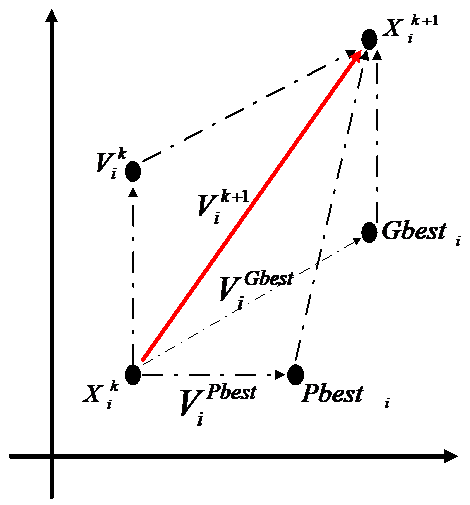Figure 2. Concept of a searching point by PSO

Where

 is current velocity of particle i at iteration k.

 is modified velocity of particle i.

 is current position of particle i at iteration k.

 is modified position of particle i.

 is velocity based on Pbest.

 is velocity based on Gbest.

Figure 3. Flow Chart of PSO

Figure 3 shows the flow chart for the optimal allocation of PSO procedure [26].

3.2.  Genetic Algorithm

A genetic algorithm (GA) is a search and optimization procedure which acts by mimicking the evolutionary principles and chromosomal processing in natural genetics. A GA begins its search with a random set of solutions usually coded in binary strings. Every solution is assigned a fitness which is directly related to the objective function of the search and optimization issue [27]. Thereafter, the population of solutions is modified to a new population by applying three operators similar to natural genetic operators- reproduction, crossover, and mutation. It works iteratively by successively applying these three operators in each generation till a termination criterion is satisfied. Over the past decade and more, GAs have been successfully applied to a wide range of problems, because of their simplicity, global perspective, and inherent parallel processing [28].

4.       Mathematical Recognition of Objective Functions

To realize the polynomial in various orders MATLAB curve fitting tool is employed. Following are mathematical expressions associated with the objective functions [29].

5.       Simulation Outcomes and Discussion

Table 1 shows the Eigen characteristic analysis of New England System with and without PSS [30].

It is observed that when PSS is not installed with generators, system shows poor damping. Some of the poorly damped types (swing modes) are shown in the following table. The real part of the Eigen value is positive.

Although the damping controller designed through evolutionary algorithms is quite robust and proved effective in all operating contingencies yet to show the efficacy of the proposed controller extreme conditions are chosen. The performance of the controller is exhibited in terms of hard situations. For this reason, here three phase disturbances are verified and speed responses of those generators are shown which are near by the disturbance locations [31].

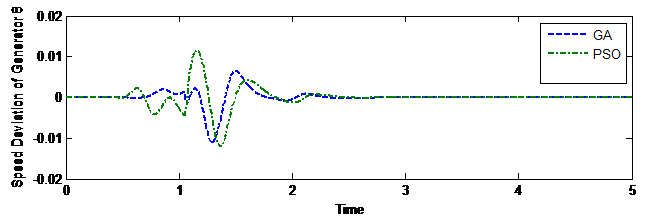Figure 4. Speed Deviation Curve of Generator 8 for disturbance at line 2-25

It can be observed from the responses of various generators that PSS tuned through GA gives less dynamic response as compared with PSO tuned PSS. Figures 5 to 8 are the speed deviation curves of various generators under dissimilar perturbations and disturbance locations [32].

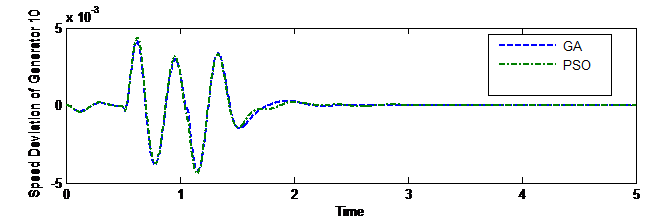Figure 5. Speed Deviation Curve of Generator 10 for disturbance at line 2-25

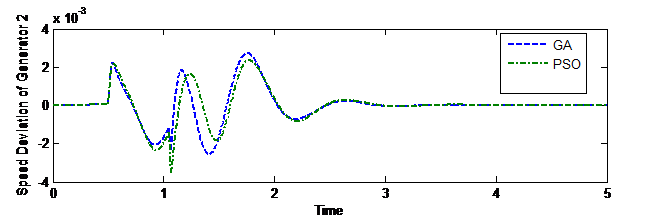Figure 6. Speed Deviation Curve of Generator 2 for disturbance at line 4-14

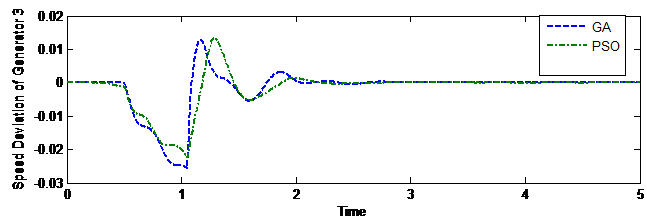Figure 7. Speed Deviation Curve of Generator 3 for disturbance at line 4-14

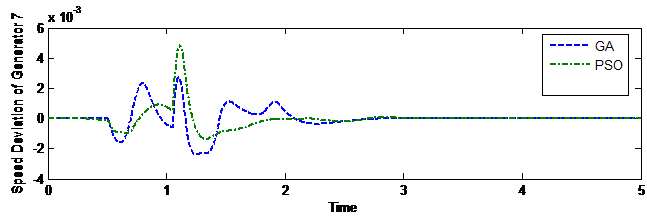Figure 8. Speed Deviation Curve of Generator 7 for disturbance at line 16-24

Table 1. Eigen Values and Damping Ratios With and Without PSS

Without PSS		With PSS
Eigen Values	Damping Ratio	Eigen Values	Damping Ratio
0.0926-i0.2063	-0.0259	-0.1823-i0.3003	0.7595
0.0926+0.2083	-0.0259	-0.1823+i0.3003	0.7595
1.3110-i0.3730	-0.0316	-0.9979-i0.0404	0.3813
1.3110+i0.3730	-0.0316	-0.9979+i0.0404	0.3813
0.2300+i4.0882	-0.0083	-1.0262-i0.7672	0.538
0.2300-i4.0882	-0.0083	-1.0262+i0.7672	0.538
0.0501-i13.863	-0.015	-11.3849-i10.7133	0.5099
0.0501+i13.863	-0.015	-11.3849+i10.7133	0.5099
0.0033-i5.3036	-0.0014	-34.7713-i59.6870	0.4307
0.0033+i5.3036	-0.0014	-34.7713+i59.687	0.4307

The factors of all 10 PSSs gained from solving optimization issue using PSO is shown in Table 2. The convergence characteristics of various optimization methods for variation of objective function and iteration is shown in Figure 8 [33].

Table 2. PSS factor for 10 Machine 39 Bus Using PSO [34-38]

Generator Number	Kstab	T1	T3
1	25.31	0.048	0.03
2	29.32	0.067	0.07
3	46.3	0.185	0.03
4	32.09	0.141	0.19
5	25.74	0.1	0.1
6	27.02	0.18	0.04
7	21.31	0.1	0.07
8	26.8	0.15	0.1
9	26.19	0.08	0.05
10	22.85	0.11	0.03

6.       Conclusion

In this article endeavor is made to implement GA and PSO for finding the optimal parameters of Power System Stabilizer (PSS) for New England Power system. From this revision following points can be accomplished:

4. Flourishing realization of conventional speed based objective functions in four dissimilar polynomials is presented in section 4. The qualified analysis of these realizations is shown with the help of dynamic responses of speed deviation curves of the generators. It is observed that linear combination of linear, quadratic and cubic polynomial gives the finest response.
5. The consequential comparison of application of two optimization methods namely GA and PSO algorithm in PSS design problem.

1. F. P. deMello and C. Concordia, “Concepts of synchronous machine stability as affected by excitation control,” IEEE Trans. Power Apparat. Syst., vol. PAS-88, pp. 316–329, 1969.
2. E. V. Larsen, and D. A. Swann, “Applying power system stabilizers, parts I, II & III,” IEEE Trans. Power App. & Sys., vol. PAS-100, no. 6, pp. 3025-3046, June 1981.
3. Michael J. Basler, Richard C. Schaefer, “Understanding power system stability”, 58th Annual Conference for Protective Relay Engineers, 2005, Volume , Issue , 5-7 April 2005, pp. 46-67.
4. BoonsermChangaroon, Suresh Chandra Srivastava and DhadbanjanThukaram, “A Neural Network Based Power System Stabilizer Suitable for On-Line Training—A Practical Case Study for EGAT System” IEEE Transaction on Energy Conversion, Volume 15, Issue 1, Mar 2000, pp. 103 – 109.
5. A. M. Sharaf, T. T. Lie and H. B. Gooi “Neural Network Based Power System Stabilizers”, Proceedings of the IEEE ANNES’93, New Zealand, June 1993. pp. 306-309.
6. Ravi Segala, Avdhesh Sharma and M.L. Kothari, “A self-tuning power system stabilizer based on artificial neural network” Electrical power & energy systems, 2004, vol. 26, no6, pp. 423-430.
7. DK Chaturvedi and Malik OP. Neuro fuzzy power system stabilizer. IEEE Trans Energy Convers 2008;23:887–94.
8. Y. Zhang, G. P. Chen, 0. P. Malik, G. S. Hope, “An artificial neural network based adaptive power system stabilizer”, IEEE Transactions on Energy Conversion, Vol. 8, No. 1, March 1993.
9. A. Doi and S. Abe, “Coordinated Synthesis of Power System Stabilizers in Multi-machine Power Systems”, IEEE Transactions on Power Apparatus and Systems, vol. 103, no. 6, pp. 1473-1479, 1984.
10. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of IEEE international conference on neural networks, vol. IV. Perth, Australia, November 29–December 1; 1995. p. 1942–8.
11. K. W. Wang, C. Y. Chung, C. T. Tse, and K. M. Tsang, “Multimachine Eigenvalue Sensitivities of Power System Parameters”,IEEE TRANSACTIONS ON POWER SYSTEMS, VOL. 15, NO. 2, MAY 2000.
12. C. Y. Chung, Member, IEEE, K. W. Wang, C. T. Tse, Member, IEEE, X. Y. Bian, and A. K. David, Fellow, IEEE, “Probabilistic Eigenvalue Sensitivity Analysis and PSS Design in Multimachine Systems”, IEEE TRANSACTIONS ON POWER SYSTEMS, VOL. 18, NO. 4, NOVEMBER 2003.
13. Seung-MookBaek, Student Member, IEEE, Jung-Wook Park, Member, IEEE, and Ian A. Hiskens, Fellow, IEEE, “Optimal Tuning for Linear and Nonlinear Parameters of Power System Stabilizers in Hybrid System Modeling”, IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 45, NO. 1, JANUARY/FEBRUARY 2009.
14. Y. L. Abdel-Magid, & M. A. Abido, “Optimal multiobjective design of robust PSSs using genetic algorithms,” IEEE Trans. Power Sys., vol. 18, no. 3, pp.1125-1132, August 2003.
15. M. A. Abido, “Optimal design of PSSs using particle swarm optimization,” IEEE Trans. Energy Con., vol. 17,no. 3, pp. 406-413, September 2002.
16. M. A. Abido, “A novel approach to conventional power stabilizer design using tabu search,” Int. J. Electric Power Energy Sys. vol. 21, pp. 443-454, June 1999.
17. M. A. Abido, “Robust design of multimachine PSSs using simulated annealing,” IEEE Trans. Energy Con., vol. 15,no. 3, pp. 297-304, September 2000.
18. H. Shayeghi and S. Jalilzadeh, “Robust PSS Design Using Chaotic Optimization Algorithm for a Multimachine Power System”, IEEE Trans. Energy Con.978-1-4244-3388-9/09.
19. D.K. Sambariya and R. Prasad, “Robust tuning of power system stabilizer for small signal stability enhancement using metaheuristic bat algorithm”,Electrical Power and Energy Systems 61 (2014) 229–238.
20. Bonabeau, E., Dorigo, M., &Theraulaz, G. (1999). Swarm intelligence: From natural to artificial systems. New York, NY, USA: Oxford University Press, Inc..
21. Kassabalidis, I., El-Sharkawi, M. A., II Marks, R. J., Arabshahi, P., & Gray, A. A. (2001). Swarm intelligence for routing in communication networks. Global Telecommunications Conference, GLOBECOM ’01 (Vol. 6, pp. 3613–3617).IEEE.
22. Kennedy, J., &Eberhart, R. (1995). Particle swarm optimization. In Proceedings of the 1995 IEEE international conference on neural networks (Vol. 4, pp. 1942–1948).
23. Karaboga, D., &Akay, B. (2009). A comparative study of artificial bee colony algorithm. Applied Mathematics and Computation, 0096-3003, 214(1), 108–132.
24. Passino, K. M. (2002). Bio mimicry of bacterial foraging for distributed optimization and control. IEEE Control Systems Magazine, 22(3), 52–67.
25. Hossein, A., & Hossein-Alavi, A. (2012). Krill herd: A new bio-inspired optimization algorithm. Communications in Nonlinear Science and Numerical Simulation, 17,4831–4845.
26. Yang, E., Barton, Nick H., Arslan, T., & Erdogan, Ahmet T. (2008). A novel shifting balance theory-based approach to optimization of an energy-constrained modulation scheme for wireless sensor networks. In Proceedings of the IEEE congress on evolutionary computation, CEC 2008, June 1–6, 2008 (pp. 2749–2756).Hong Kong, China: IEEE.
27. Rajabioun, R. (2011). Cuckoo optimization algorithm. Applied Soft Computing, 11,5508–5518.
28. H. Othman, and et al., “On the design of robust power system stabilizers,” IEEE Proc of 28th conf on Dec. & control, pp. 1853-1857, December 1989.
29. Y. Yu, and Q. Li, “Pole-placement power system stabilizers design of an unstable nine-machine system, IEEE Trans. Pr Sys., vol. 5, no. 2, pp.353-358, May 1990.
30. Julio C. R. Ferraz, Member, IEEE, Nelson Martins, Fellow, IEEE and Glauco N. Taranto, Member, IEEE, “Coordinated Stabilizer Tuning in Large Power Systems Considering Multiple Operating Conditions”,1-4244-1298-6/2007 IEEE.
31. P. S. Rao and I. Sen, “Robust pole placement stabilizer design using linear matrix inequalities,” IEEE Trans. Power Syst., vol. 15, no. 1, pp. 313–319,2000.
32. IEEE Committee Report on excitation systems (1981).
33. M. J. Gibbard,: “Robust design of fixed-parameter power system stabilizers over a wide range of operating conditions”, IEEE Trans. Power Syst., Vol. 6, No.2, pp.794-800, 1991.
34. P. Kundur, “Power system stability and control” McGraw Hill, New York, 1994.
35. Erik Cuevas, Miguel Cienfuegos, Daniel Zaldívar, Marco Pérez-Cisneros, “A swarm optimization algorithm inspired in the behavior of the social-spider”,Expert Systems with Applications 40 (2013) 6374–6384.
36. James J.Q. Yu, Victor O.K. Li: “A Social Spider Algorithm for Global Optimization” Technical Report No. TR-2003-004, Dept. of Electrical & Electronic Engineering, the University of Hong Kong, Oct 2013.
37. Chatterjee, S. and Laudato, M. (1997). Genetic algorithms in statistics: procedures and applications. Commun. Statist. Simula., 26 (4), 1617-1630.
38. J. Chow, Graham Rogers. “Power system toolbox.” Cherry Tree scientific Software, Available: http://www. ecse. rpi. Edu/pst/PST. Html,2000.

(Click to view)

(Click to view)

No. of Downloads Per Month

No. of Downloads Per Country