1.       Introduction

Recommender system as defined from the perspective of E commerce as a tool that helps users search through records of knowledge which is related to users interest and preference for a recommender system to implement its core function of identifying useful items for the user, [1, 2]. In [3] RSs is defined as a means of assisting and augmenting the social process of using recommendations of others to make choices when there is no sufficient personal knowledge or experience of the alternatives.

 (RS) must predict that an item is worth recommending [4, 5]. In view of that, recommendation systems of late have become an interesting field, as they play an exquisite role in various automatic recommendation systems, and are nowadays pervasive in various domains such as recommendation of books at Amazon, music and movies recommendation at Netflix as an algorithm form tackling the information over load problem. Some of the main specific constraints or digital-age dilemmas of Recommender Systems (RSs) are; data sparsity, cold-start and issues. To overcome such problems, Matrix Factorization methods have been applied extensively by various researchers in the field. [6]-[8]. In recent times, additional sources of information are integrated into RSs. As a result, a lot of research in this field are being carried about mainly with Matrix factorization methods such as social matrix factorization (Social MF), which combines ratings with social relations [9]-[14]. Another research thread is Topic Matrix Factorization methods which combine latent factors in ratings with latent topics in item reviews [15]. In [16, 10], the authors suggested other sources of information like reviews which justify the rating of a user, and ratings which are associated with item attributes hidden in reviews producing extraordinary results but at the cost of training data and time. In this wise, we propose that, omitting such information does not aid recommendation accuracy. As a result, such problems according to research could be well taken care of through tensor decomposition as propounded by [17] and our motivation for this paper is strongly tied to these reasons. Various tensor decomposition methods have been proposed. The CANDECOMP/PARAFAC decomposition, shorted as CP decomposition, is a direct extension of low-rank matrix decomposition to tensors; and it can be regarded as a special case of Probabilistic Tensor Factorization (PTF) [18], inspired by probabilistic latent factor models [19, 20], has been proposed by various researchers as an effective tool for tackling recommendation problems [21, 22]. The era of big data has also witnessed the explosion of tensor datasets, while the large scale PTF analysis is important to accommodate the increasing datasets. A comprehensive overview can be found from the survey paper by [23]. There is therefore the need for us to solicit for tensor decomposition analysis that is able to extract hidden patterns from multi-way datasets. The core concept of senti-PTF is to capture additional sources of information occasionally neglected in various recommendation models which could efficiently improve prediction performance in RSs. The key contribution of our model is that it integrates all available data sources, that is, it provides a joint model of user, product I.D, ratings, reviews and review helpfulness.

1. Providing an effective way to exploit ratings, reviews and relations to overcome cold-start problems tightly.
2. We propose a new framework; senti-PTF which is effective in terms of prediction through error detection and solves sparsity problems.

The rest of this paper is organized as follows; Tensor

Decomposition Preliminaries are given in Section 2. In Section 3, we present the details of the experiments with datasets. In Section 4, Concluding remarks with a discussion of some future work are in the final section. Matrix Factorization and its application to personalized recommendation demonstrated the effectiveness of directly modelling all the dimensions simultaneously in a unified framework. These among other works presupposes that, tensor decomposition models performed well in terms of prediction efficiency and effectiveness compared to the various matrix factorization algorithms, in particular application  to massive data processing [24]-[26]. However, the numerous literature concerning the subject.

1.2 Problem Statement

Regardless of the various attempt made by researchers on the subject matter; Collaborative Filtering models, they suffer from Sparsity; due to sparse rating matrix. Cold-Start; as they perform poorly on cold users and cold items for which there are no or few data. User feedback is intended to discover latent product and user dimensions. Unfortunately, traditional methods often discard review text, which makes user and product latent dimensions difficult to interpret, mainly due to the fact that, the very text that justifies a user’s rating is relegated. In our opinion, ignoring rich source of information is a major shortcoming of existing works on recommender systems

1.3 Related Work

Tensor factorization methods are useful tools in recommendation systems. One prominent representative Factor-based method for recommendation systems is Probabilistic Tensor Factorization (PTF) which has been envisaged by quite a number of researchers in the recommendation system field. Tensor Factorization (BPTF) was also used to enhance prediction accuracy and recommendation using sales data by [27]. [28] also proposed the PTF model which was naturally applicable to incomplete tensors to provide both point estimate and multiple imputation for the missing entries. Tensor factorization [29] for Precision Medicine in Heart Failure with Preserved Ejection Fraction was effective. [30] in his Probabilistic polyadic factorization and its application to personalized recommendation demonstrated the effectiveness of directly modelling all the dimensions simultaneously in a unified framework. These among other works presupposes that, tensor decomposition models performed well in terms of prediction efficiency and effectiveness compared to the various matrix factorization algorithms, in particular application  to massive data processing [31]-[33]. However, the numerous literature concerning the subject.

2.0 Proposed Sentiment-based Tensor Analysis

We propose a tensor decomposition approach to solve the sparsity, and cold-start problems of collaborative filtering algorithm making use of review sentiments and rating scores adopting Probabilistic Tensor Factorization. The main idea is to capture the latent structure of a tensor through a probabilistic factorization framework, and the latent structure is used for prediction. We jointly model ratings with review sentiments scores and model our data with probabilistic tensor factorization algorithm. In particular, CP decomposition which factorizes a tensor into a summation of rank-one tensors, where A, B and C are the latent factors. We propose probabilistic tensor factorization (PTF), which is an instance of CANDECOMP/PARAFAC (CP) tensor decomposition [34], which is a commonly used tensor model for factorization.

2.        Equations

PTF’s performance, we process the data into three 3rd order tensors, where each  mode correspond to IDs, users and reviews, and also modelled ratings with item IDs, users and ratings respectively denoted by the tensor ABC as shown in our probabilistic model. The ratings range from 1 to 5, whiles the review sentiment were processed to 0 and 1 representing negative and positive sentiments. Tensor factorization techniques have gained popularity and have become the standard recommender approaches due to their accuracy and scalability [35]. They have probabilistic interpretation with Gaussian noise. Our model Senti-PTF combines our sentiment algorithm with probabilistic Tensor factorization framework. For Probabilistic Tensor S of size [I, J, K] where each entry is indexed as (i, j, k), and assume there is a D-dimensional latent factor A_i, B_j and C_k corresponding to each i, j and k respectively. In other words, for each dimension of the tensor, we have a latent factor matrix (A_i _D), (B_j _ D), and (C_k _D) respectively. The distribution of the unknown entry (I, j, k) given the observed tensor S is generated from Multivariate Gaussian Distribution. Given S the learning task is to model parameter theta such that the likelihood function is given by;

Where .

Given the Tensor S, the parameter θ is learned in such a way that p (S|θ) in the previous equation maximizes. Expectation Maximization is used for the posterior over latent variables P (A, B, C, S (θ)). The estimated model posterior for Finite Dimension Inference (FDI) is intractable. We therefore propose approximation inference by factorizing q(A,B,C| ) to the posterior P(A,B,C|0) more importantly;

q(A,B,C| ) =

where

 are approximation variational parameters.

All approximation parameters are D-dimensional vectors and diag (w_ai) denotes a square matrix with the w_ai on the diagonal. Given q (A,B,C|θ^’). if we apply Jensen’s inequality, it produces a lower bound to the original log likelihood of the tensor S [36]

2.1 Algorithm

1: Input: S ∈ Tx,y,z, h

2: Output: S^h∈ T

3.X^h×y×z

4: Initialize x = 0

5: for H = 1,…,h

6: Sh← S (x_one,+x;x_two;,;)

7: end for

3.       Experiments

Our experiment is designed to study the accuracy and efficiency of the senti-PTF, rat-PTF and baselines on social media review datasets which are publicly available. All the experiments are run on a Processor AMD E26110 APU with AMD Radeon R2 Graphics, 1500 Mhz, 4 Core(s), 4 Logical Processor(s) and 12GB of RAM. (a) Datasets and Parameter Settings: The real word tensor data used in our experiments are public collaborative filtering datasets; Amazon Datasets, which contains product reviews and metadata from Amazon, including 142.8 million reviews spanning May 1996 to July 2014 [37]. This dataset includes. Reviews (ratings, text, helpfulness votes), product metadata (descriptions, category information, price, brand, and image features) and links. In order to study senti-PTF’s performance, we process the data into three 3rd order tensors, where each mode correspond to IDs, users and reviews, and also modelled ratings with item IDs, users and ratings respectively denoted by the tensor ABC as shown in our probabilistic model. The ratings range from 1 to 5, whiles the review sentiments were processed to 0 and 1 representing negative and positive sentiments.

3.1 Error Detection

For comparison, we implement and report the performance of senti-PTF and rat-PTF prediction. For the consistency of expression we still use “customer” and “item” to represent reviewers of automotive products. We estimate error rates on sentiments and ratings expressed, to assess the performance of our model and had the following results (figure1): The error graph shows how our algorithm; senti-PTF and rat-PTF performed. Senti-PTF performed better than rat-PTF in terms of prediction performance

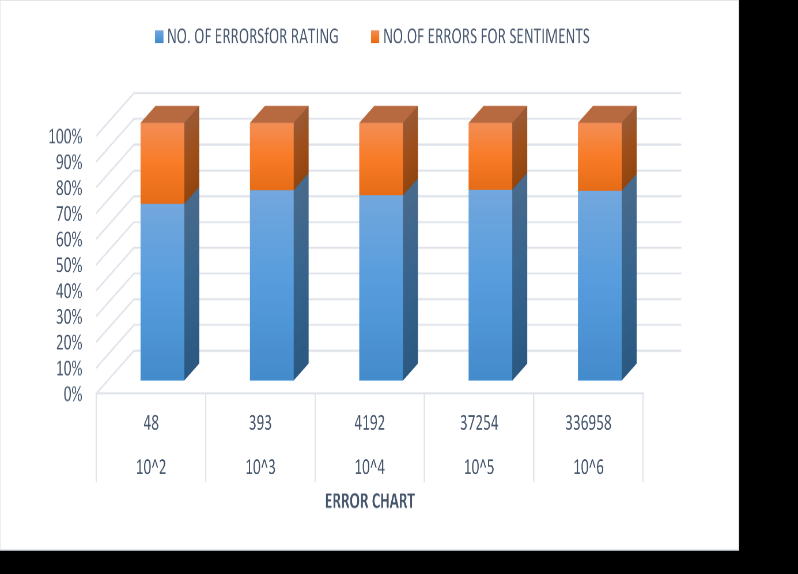Figure 1 Error detection for senti-PTF and rat-PTF

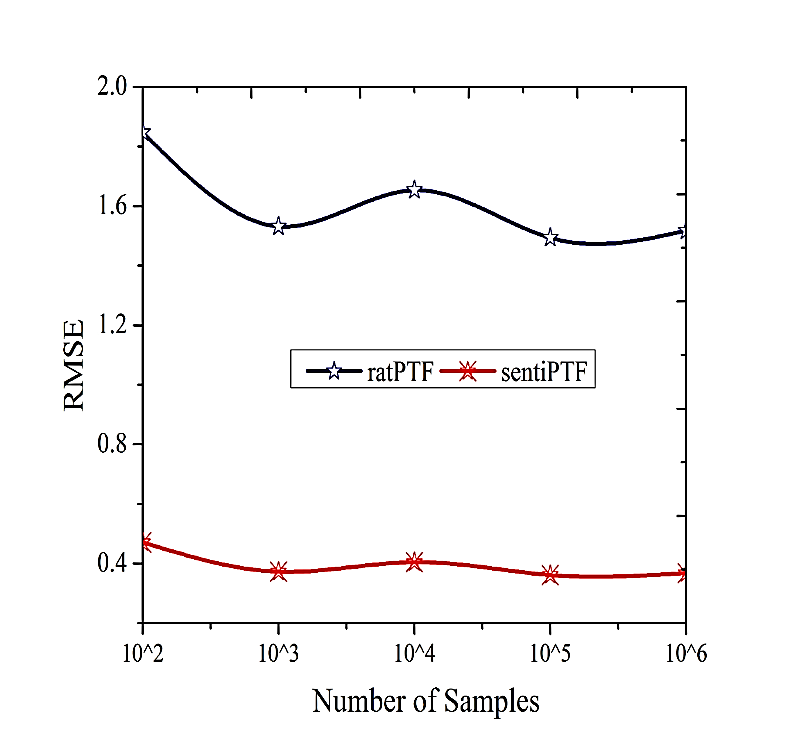Figure 2 Root mean square error rate

4.       Conclusion

 A unified framework rat-PTF and senti-PTF by aligning latent factors and topics is proposed to perform Probabilistic Tensor Factorization for effective rating and sentiment prediction. In this paper, experiments on real world data sets demonstrate that our senti-PTF model outperforms the traditional CP decomposition, exploiting review sentiment beyond ratings can significantly improve recommender performance in terms of RMSE (figure2). We therefore propose Sentiment based Tensor Analysis approach in recommendation as it solves the cold start, improves prediction efficiently and solves scalability problems of the big data era. Model integration could be envisaged in our future work [38]. Figure1 demonstrates sent-PTF achieves better performance as the tensor size increases on the Amazon datasets. The result directly sheds light on the necessity of a senti- PTF solution.

5.       Conflict of Interest

We declare that, there is no conflict of interest to the publishing of this work.

Acknowledgment

This work is supported in part by the applied basic research programs of Sichuan Province (2015JY0043), the Fundamental Research Funds for the Central Universities (ZYGX2015J154, ZYGX2016J152, ZYGX2016J170), programs of international science and technology cooperation and exchange of Sichuan Province (2017HH0028), Key research and development projects of high and new technology development and industrialization of Sichuan Province(2017GZ0007)

1. D. Jannach, P. Resnick, A. Tuzhilin, M. Zanker, Recommender systems|: beyond matrix completion, Communications of the ACM 59 (11) (2016) 94{102.
2. D. Kotkov, S.Wang, J. Veijalainen, A survey of serendipity in recommender systems, Knowledge-Based Systems 111 (2016) 180{192}
3. D. Lamprecht, M. Strohmaier, D. Helic, A method for evaluating the navigability of recommendation algorithms, Springer, 2016, pp. 247{259.
4. B. Paudel, F. Christo_el, C. Newell, A. Bernstein, Updatable, accurate, diverse, and scalable recommendations for interactive applications, ACM Transactions on Interactive Intelligent Systems (TiiS) 7 (1) (2016) 1.
5. R. Frey, D. Worner, A. Ilic, Collaborative filtering on the blockchain: A secure recommender system for ecommerce.
6. J. Wei, J. He, K. Chen, Y. Zhou, Z. Tang, Collaborative filtering and deep learning based recommendation system for cold start items, Expert Systems with Applications 69 (2017) 29{39.
7. G.-N. Hu, X.-Y. Dai, Y. Song, S.-J. Huang, J.-J. Chen, A synthetic approach for recommendation: combining ratings, social relations, and reviews, arXiv preprint arXiv:1601.02327.
8. G. Guo, J. Zhang, D. Thalmann, Merging Trust in collaborative filtering to alleviate data sparsity and cold start, Knowledge-Based Systems 57 (2014)57{68.
9. Q. Yuan, L. Chen, S. Zhao, Factorization vs. regularization,Proceedings of the fifth ACM conference on Recommender systems, ACM, 2011, pp. 245{252.
10. Y. Zhang, Grorec: a group-centric intelligent recommender system integrating social, mobile and big data technologies, IEEE Transactions on Services Computing 9 (5) (2016) 786{795.
11. J. Tang, X. Hu, H. Gao, H. Liu, Exploiting local and global social context for recommendation, in: IJCAI, 2013, pp. 264{269.
12. M. Bergen, S. Dutta, O. C. Walker Jr, Agency relationships in marketing: A review of the implications and applications of agency and related theories, The Journal of Marketing (1992) 1{24.
13. T. Chen, R. Xu, Y. He, Y. Xia, X. Wang, Learning user and product distributed representations using a sequence model for sentiment analysis, IEEE Computational Intelligence Magazine 11 (3) (2016) 34{44.
14. C. Zheng, E. Haihong, M. Song, J. Song, Cmptf: Contextual modeling probabilistic tensor factorization for recommender systems, Neurocomputing 205 (2016) 141{151.
15. F. Buettner, N. Pratanwanich, J. C. Marioni, O. Stegle, Scalable latentfactor models applied to single-cell rna-seq data separate biological drivers from confounding effects, bioRxiv (2016) 087775.
16. J. Chen, X. Luo, Y. Yuan, M. Shang, Z. Ming, Z. Xiong, Performance of latent factor models with extended linear biases, Knowledge-Based Systems.
17. G. Li, Z. Xu, L. Wang, J. Ye, I. King, M. Lyu, Simple and efficient parallelization for probabilistic temporal tensor factorization, arXiv preprint arXiv:1611.03578.
18. A. Sapienza, A. Bessi, E. Ferrara, Non-negative tensor factorization for human behavioral pattern mining in online games, arXiv preprint arXiv: 1702.05695.
19. C. Meneveau, I. Marusic, Turbulence in the era of big data: Recent experiences with sharing large datasets, Springer, 2017, pp. 497{507.
20. Q. Liu, H. Jiang, Z.-H. Ling, S.Wei, Y. Hu, Probabilistic reasoning via deep learning: Neural association models, arXiv preprint arXiv:1603.07704.
21. E. E. Papalexakis, C. Faloutsos, Unsupervised tensor mining for big data practitioners, Big Data 4 (3) (2016) 179
22. E. E. Papalexakis, C. Faloutsos, N. D. Sidiropoulos, Tensors for data mining and data fusion: Models, applications, and scalable algorithms, ACM Transactions on Intelligent Systems and Technology (TIST) 8 (2) (2016)
23. T.-L. Lee, Y.-C. Kuo, Computing the unique candecomp/parafac decomposition of unbalanced tensors by homotopy method, arXiv preprint arXiv: 1607.07128.
24. W.-S. Chin, Y. Zhuang, Y.-C. Juan, C.-J. Lin, A fast parallel stochastic gradient method for matrix factorization in shared memory systems, ACM Transactions on Intelligent Systems and Technology (TIST) 6 (1) (2015) 2.
25. P. R. Kumar, P. Varaiya, Stochastic systems: Estimation, identification, and adaptive control, SIAM, 2015. pp. 785
26. A. Cichocki, D. Mandic, L. De Lathauwer, G. Zhou, Q. Zhao, C. Caiafa, H. A. Phan, Tensor decompositions for signal processing applications: From two-way to multiway component analysis, IEEE Signal Processing Magazine 32 (2) (2015) 145{163.
27. B. Cyganek, S. Gruszczy_nski, Hybrid computer vision system for drivers’ eye recognition and fatigue monitoring, Neurocomputing 126 (2014) 78{94.
28. X. Yang, Y. Guo, Y. Liu, and H. Steck, “A survey of collaborative filtering based social recommender systems,” Comput. Commun., vol. 41, pp. 1–10, 2014.
29. M. Rossetti, F. Stella, and M. Zanker, “Analyzing user reviews in tourism with topic models,” Inf. Technol. Tour., vol. 16, no. 1, pp. 5–21, 2016.
30. X. Amatriain, J. Basilico, Past, present, and future of recommender systems: An industry perspective, in: Proceedings of the 10th ACM Conference on Recommender Systems, ACM, 2016, pp. 211{214.
31. H. Ma, D. Zhou, C. Liu, M. R. Lyu, I. King, Recommender systems with social regularization, in: Proceedings of the fourth ACM international conference.
32. Q. Yuan, L. Chen, S. Zhao, Factorization vs. regularization: fusing heterogeneous social relationships in top-n recommendation, in: Proceedings of the _fth ACM conference on Recommender systems, ACM, 2011, pp.245{252}.
33. J. McAuley, R. Pandey, J. Leskovec, Inferring networks of substitutable and complementary products, in: Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, 2015, pp. 785{794.
34. H. Wang, N. Wang, D.-Y. Yeung, Collaborative deep learning for recommender systems, in: Proceedings of the 21th ACM SIGKDD International Conference.
35. A. M. Elkahky, Y. Song, and X. He, “A Multi-View Deep Learning Approach for Cross Domain User Modeling in Recommendation Systems,” in Proceedings of the 24th International Conference on World Wide Web – WWW ’15, 2015.
36. J. McAuley, J. Leskovec, Hidden factors and hidden topics: understanding rating dimensions with review text, in: Proceedings of the 7th ACM conference on Recommender systems, ACM, 2013, pp. 165{172
37. G. Shani, A. Gunawardana, Evaluating recommendation systems, in: Recommender systems handbook, Springer, 2011.
38. Y. Koren and R. Bell, “Advances in collaborative filtering,” in Recommender systems handbook, Springer, 2015, pp. 77–118.

(Click to view)

(Click to view)

No. of Downloads Per Month

No. of Downloads Per Country