Travelling Wave Solutions of Coupled Burger’s Equations of Time-Space Fractional Order by Novel (Gʹ/G)-Expansion Method
Volume 2, Issue 4, Page No 8-13, 2017
Author’s Name: Rashida Hussain, Tayyiaba Rasoola), Asghar Ali
View Affiliations
Department of Mathematics, Mirpur University of Science and Technology (MUST), Mirpur-10250 (AJK), Pakistan
a)Author to whom correspondence should be addressed. E-mail: tayba481@yahoo.com
Adv. Sci. Technol. Eng. Syst. J. 2(4), 8-13 (2017); ![]() DOI: 10.25046/aj020402
DOI: 10.25046/aj020402
Keywords: Fractional complex transformation, Fractional derivatives, Fractional order coupled Burger’s equations, Novel (Gʹ/G)-expansion method
Export Citations
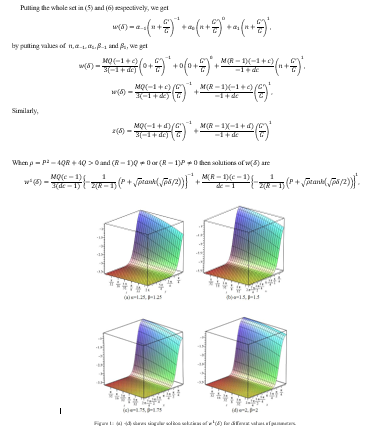
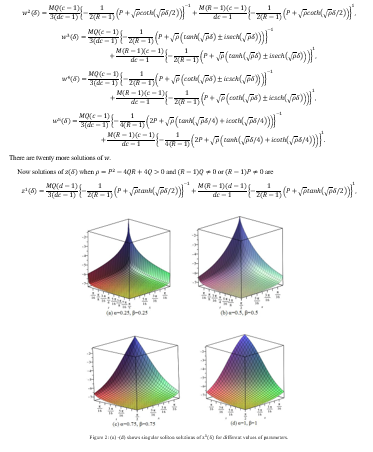
In this paper, Novel (Gʹ/G)-expansion method is used to find new generalized exact travelling wave solutions of fractional order coupled Burger’s equations in terms of trigonometric functions, rational functions and hyperbolic functions with arbitrary parameters. For the conversion of the partial differential equation to the ordinary differential equation, complex transformation method is used. Novel (Gʹ/G)-expansion method is very effective and provides a powerful mathematical tool to solve nonlinear equations. Moreover, for the representation of these exact solutions we have plotted graphs for different values of parameters which were in travelling waveform.
Received: 09 March 2017, Accepted: 29 March 2017, Published Online: 07 April 2017
1. Introduction
Fractional complex transformation as in [1] is utilized for transformation of nonlinear fractional order partial differential equations into nonlinear ordinary differential equations. The one-dimensional case of Burger’s equation was introduced by a Dutch scientist J. M. Burger in 1939 see [2], its general form is given as
Afterward, new type of Burger’s equation was presented in further research named as time-space fractional order coupled Burger’s equations [3], which has the form
where
An assortment of approaches occurs for nonlinear equations which gives their travelling wave and numerical solutions. Wang et al. introduced (Gʹ/G)-expansion method [4]. This method was further reached out for coupled Burger’s equations by Younas et al. [3]. In this article Novel (Gʹ/G)-expansion method has been utilized to discover travelling wave solutions of nonlinear space and time fractional order coupled Burger’s equations.
1.1. Fractional complex transformation
Fractional complex transform is the unobtrusive way for the transformation of the fractional order differential equation into integer order differential equation. This simplifies the rest of the procedure towards a solution. Presently consider
where L, M, N and O are constants.
Let the fractional complex transformation in nonlinear fractional order coupled Burger’s equations be defined as
1.2. Travelling wave solution
Travelling wave solution was used for transformation of partial differential equations into ordinary differential equations. For this purpose, we consolidate two independent variables into one independent variable known as travelling wave variable x [5].
Travelling wave solution of nonlinear partial differential equation
Conclusion
Novel (Gʹ/G)-expansion method is an effective method for finding exact solutions of the fractional order partial differential equation. As an application, exact solutions have been all around got for time-space fractional order coupled Burger’s equations. The fractional complex transformation used as a part of the exhibited work is very momentous. By utilizing this fractional transformation, fractional order partial differential equation can be converted into the integer order ordinary differential equation. Graphical portrayals insure that the required solutions are travelling wave solutions. Novel (Gʹ/G)-expansion method is an influential mathematical tool for solving the nonlinear partial differential equations.
- J. H. He, S. K. Elagan and Z. B. Li, “Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus,” Physics Letters. A, 376( 4): 257–259 (2012).
- J. M. Burgers, “Mathematical examples illustrating relations occurring in the theory of turbulent fluid motion,” verhand. kon. neder. akad. wetenschappen, afd. natuurkunde, eerste sectie, 17: 1-53 (1939).
- Muhammad Younis, Asim Zafar, Kalim-Ul-Haq and Muhammad Rahman, “Travelling wave solutions of fractional order coupled Burger’s equations by (Gʹ/G)-expansion method,” American Journal of Computational and Applied Mathematics, 3(2): 81 (2013).
- M. L. Wang, X. Li and J. Zhang, “The (Gʹ/G)-expansion method and travelling wave solutions of nonlinear evolution equations in Mathematical Physics,” Phys. Lett. A, 372: 417-423 (2008).
- Muhamad Abdel Rehim Selim Ibrahim Elshobaki, “Travelling wave solutions of reaction-diffusion equations coupled with shallow water equations,” Hamburg, 9-10 (2012).
- A. Biswas, M. S. Ismail, “1-Soliton solution of the coupled KdV equation and Gear-Grimshaw model,” Appl. Math. Comp., 216: 36623670 (2010).
- Yong Chen and Hong-Li An, “Numerical solutions of coupled Burger’s equations with time and space-fractional derivatives,” Applied Mathematics and Computation, 200: 87-95 (2008).
- Muhammad Shakeel, Qazi Mehmood Ul-Hussain, Jamshad Ahmad and Tauseef Naqvi, “Exact solutions of the time fractional BBM-Burger’s equation by Novel (Gʹ/G)-expansion method,” Hindawi Publishing Corporation, Advances in Mathematical Physics, 181594: 1-15 (2014).
- G. Jumarie, “Modified Riemann-Liouville Derivative and Fractional Taylor Series of Non-Differentiable Functions Further Results,” Computers and Mathematics with Applications, 51: 1369 (2006).
- Z. Li and J. He, “Fractional complex transform for fractional differential equations,” Mathematical and Computational Applications, 15(2): 970-973 (2010).
- J. D. Cole, “On a quasi-linear parabolic equation occurring in aerodynamics,” quart. appl. math., 9: 225-236 (1951).
- E. Hopf, “The partial differential equation, u_t+uu_x=u_xx,” comm. Pure appl. math., 3: 201-230 (1950).
- S. Zhu, “The generalizing Riccati equation mapping method in nonlinear evolution equation: Application to (2+1)-dimensional Boiti-Leon-Pempinelle equation,” Chaos, Solitons and Fractals, 37(5): 1335-1342 (2008).
Citations by Dimensions
Citations by PlumX
Google Scholar
Scopus
Crossref Citations
- Tayyiaba Rasool, Rashida Hussain, Mohammed A. Al Sharif, W. Mahmoud, M. S. Osman, "A variety of optical soliton solutions for the M-truncated Paraxial wave equation using Sardar-subequation technique." Optical and Quantum Electronics, vol. 55, no. 5, pp. , 2023.
- Tayyiaba Rasool, Rashida Hussain, Hadi Rezazadeh, Dariush Gholami, "The plethora of exact and explicit soliton solutions of the hyperbolic local (4+1)-dimensional BLMP model via GERF method." Results in Physics, vol. 46, no. , pp. 106298, 2023.
- Aly R. Seadway, Asghar Ali, Ahmet Bekir, Adem C. Cevikel, Özkan Güner, "Novel exact wave solutions of the (4+1)-dimensional Boiti–Leon–Manna–Pempinelli model via application of three mathematical methods." Optical and Quantum Electronics, vol. 56, no. 7, pp. , 2024.
- Rashida Hussain, Tayyiaba Rasool, Asghar Ali, Sara Javed, "Retrieval of Chaotic structure along with P-test to Truncated M-fractional Paraxial wave model." Franklin Open, vol. 11, no. , pp. 100251, 2025.
- Shao-Wen Yao, Tayyiaba Rasool, Rashida Hussain, Hadi Rezazadeh, Mustafa Inc, "Exact soliton solutions of conformable fractional coupled Burger’s equation using hyperbolic funtion approach." Results in Physics, vol. 30, no. , pp. 104776, 2021.
- Aniqa Zulfiqar, Jamshad Ahmad, "Dynamics of new optical solutions of fractional perturbed Schrödinger equation with Kerr law nonlinearity using a mathematical method." Optical and Quantum Electronics, vol. 54, no. 3, pp. , 2022.
- M. Ali Akbar, Farah Aini Abdullah, Mst. Munny Khatun, "Comprehensive geometric-shaped soliton solutions of the fractional regularized long wave equation in ocean engineering." Alexandria Engineering Journal, vol. 72, no. , pp. 593, 2023.
- Tayyiaba Rasool, Rashida Hussain, Hadi Rezazadeh, Asghar Ali, Ulviye Demirbilek, "Novel soliton structures of truncated M-fractional (4+1)-dim Fokas wave model." Nonlinear Engineering, vol. 12, no. 1, pp. , 2023.
No. of Downloads Per Month
No. of Downloads Per Country