Optimizing the Decoding Complexity of PEG-Based Methods with an Improved Hybrid Iterative/Gaussian Elimination Decoding Algorithm
Volume 2, Issue 3, Page No 578-586, 2017
Author’s Name: Reem Alkanhel1, a), Marcel Adrian Ambroze2
View Affiliations
1Department of Information Technology, Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia
2Department of Computing, Electronics and Mathematics, Plymouth University, United Kingdom
a)Author to whom correspondence should be addressed. E-mail: rialkanhal@pnu.edu.sa
Adv. Sci. Technol. Eng. Syst. J. 2(3), 578-586 (2017); ![]() DOI: 10.25046/aj020374
DOI: 10.25046/aj020374
Keywords: Hybrid decoding, Early stopping criterion, Group integrity, Missing tag recovery, Progressive edge-growth (PEG) methods
Export Citations
This paper focuses on optimizing the decoding complexity of the progressive-edge-growth-based (PEG-based) method for the extended grouping of radio frequency identification (RFID) tags using a hybrid iterative/Gaussian elimination decoding algorithm. To further reduce the decoding time, the hybrid decoding is improved by including an early stopping criterion to avoid unnecessary iterations of iterative decoding for undecodable blocks. Various simulations have been carried out to analyse and assess the performance achieved with the PEG-based method under the improved hybrid decoding, both in terms of missing recovery capabilities and decoding complexities. Simulation results are presented, demonstrating that the improved hybrid decoding achieves the optimal missing recovery capabilities of full Gaussian elimination decoding at a lower complexity, as some of the missing tag identifiers are recovered iteratively.
Received: 04 April 2017, Accepted: 15 May 2017, Published Online: 04 June 2017
1. Introduction
Checking the integrity of groups containing radio frequency identification (RFID) tagged objects or recovering the tag identifiers of missing objects is important in many activities to find missing tagged objects. Autonomous verification of a group of RFID tags is an essential feature in RFID systems, because it ensures standalone operations as well as scalability, privacy and security. This can be achieved by treating a group of tag identifiers as packet symbols which are encoded and decoded as in binary erasure channels (BECs). This paper is an extension of work originally presented in [1], by optimizing the decoding complexity of the progressive-edge-growth-based (PEG-based) method for the extended grouping of RFID tags while achieving significant missing recovery enhancements compared to other extended grouping methods presented in [2–4].
The remainder of this article is organized as follows. A brief overview of ML and IT decoding algorithms is provided in Section 2. Section 3 introduces the early termination of IT decoding, while Section 4 presents the improved HB decoding. Section 5 evaluates the performance achieved with the improved HB decoding using simulations. Conclusions and future work follow in Section 6.Various decoding algorithms are devised to recover erasures over BECs, each with different performance and complexities. The most prominent decoding algorithms are maximum likelihood (ML) and iterative (IT) decoding algorithms. ML decoding for a BEC can be implemented as Gaussian elimination (GE), which provides the optimum decoding in terms of erasure recovery capabilities at the price of high decoding complexity [5]. On the other hand, IT decoding based on belief propagation features a linear decoding complexity, but it remains suboptimal in recovering erasures, as it is affected by the existence of short cycles [6, 7]. This suggests a hybrid (HB) decoding strategy which combines the above-mentioned IT with GE decoding algorithms in order to compromise between performance and complexity. References [8–12] proposed and implemented HB decoding algorithms in BECs with the basic idea of employing IT decoding first. If the IT decoding fails to recover all the erased symbols, the GE decoding is activated to complete the decoding process and resolve the simplified system. The GE decoding algorithm can fully recover the erasures in the simplified system if the columns of the decoding matrix are linearly independent. This paper focuses on optimizing the decoding complexity of the PEG-based method using an HB decoding algorithm. To further reduce the decoding time, the HB decoding is improved by including an early stopping criterion to avoid unnecessary iterations of iterative decoding for undecodable blocks. Simulation results are presented, demonstrating that the improved HB decoding achieves the optimal missing recovery capabilities of full GE decoding at a lower complexity, as some of the missing tag identifiers are recovered iteratively.
2. Maximum Likelihood and Iterative Decoding Algorithms
2.1. Maximum Likelihood Decoding Algorithm
The ML decoding algorithm on the BEC involves solving a system of linear equations and finding the unknowns (erasures) in![]()
where TIDk` and TIDk are the arrays of lost and known symbols (tag identifiers), respectively. Similarly, Ak` is the matrix which contains the columns of A related to TIDk`, while Ak is the matrix which contains the columns of A related to TIDk. A system of linear equations has a unique solution, if and only if the columns of Ak` have full rank (i.e. they are linearly independent). This ML decoding can be implemented as GE by reducing Ak` to row echelon form. The process of the algorithm consists of two steps. The forward elimination step first reduces the system to an upper triangular form, which can be done using elementary row operations. The algorithm continues with a backward substitution step. It recursively resolves erased symbols until the solution is found. The last symbol of an upper triangular matrix is given the value of the symbol on the right-hand side. Then, this value is replaced in all the equations in which it is included. GE provides the optimum decoding in terms of erasure recovery capabilities at the price of the high decoding complexity of O(n3), where n is the number of variables [13]. GE is used to represent ML throughout this article.
2.2. Iterative Decoding Algorithm
IT decoding algorithms or message-passing algorithms are commonly used in BEC decoding [14]. IT decoding based on belief propagation features a linear decoding complexity of O(n), but it remains suboptimal in recovering erasures over the BEC, as it is affected by the existence of short cycles [6, 7]. IT decoding algorithms consist of solving (1) by recursively exchanging messages along the edges of a Tanner graph between variable nodes and check nodes. All parity check equations having only one erased symbol are found, and the erased symbols are recovered. Then, new equations which have only one erased symbol may be created and used to recover further erased symbols. The decoding process is as follows:
- Each variable node v sends the same message Mv ∈ {0, 1, e}, where e denotes the erased symbol, to each of its connected check nodes.
- If a check node receives only one e, it replaces the erased symbol with the bitwise exclusive or XOR of the known symbols in its check equation.
- Each check node c sends different messages Ec,v ∈ {0, 1, e} to each of its connected variable nodes v. These messages represent the results of the previous step.
- If the variable node of an erased symbol receives Ec,v ∈ {0,1}, the variable node updates its value to the value of Ec,v.
The IT decoding iterates the above process until all the erasure symbols are recovered successfully or until a predetermined maximum number of iterations (Imax) has passed without successful decoding [15].
3. Early Termination of Iterative Decoding
Early termination of IT decoding has been extensively researched within correcting errors introduced by channels. At each iteration, the IT decoding detects decodable blocks by checking parity check constraints. If all parity check constraints are satisfied, the decoding terminates. Otherwise, the decoding always completes Imax iterations for undecodable blocks. The decoding time and complexity increases linearly with the number of decoding iterations. To avoid unnecessary decoding iterations when processing undecodable blocks, a proper stopping criterion is required to terminate the decoding process early and therefore to save decoding time and power consumption [16]. Different early stopping criteria have been proposed for IT decoding, aiming to detect undecodable blocks and to stop the decoding process in its early stage. These criteria can be divided into two types. One type utilizes log-likelihood ratios (LLRs), for example the criterion in [17]. It identifies undecodable blocks using variable node reliability, which is the addition of the absolute values of all variable node LLRs. The decoding process is stopped if the variable node reliability remains unchanged or is decreased within two consecutive iterations. This is a consequence of the observation that a consistent increase of the variable node reliability is expected from a decodable block. The criterion is disabled if the variable node reliability is larger than a channel-dependent threshold. Similar criteria have been proposed in [18–20] which monitor the convergence of the mean magnitude of the LLRs at the end of each iteration to identify undecodable blocks. The other type of criteria are those which observe the numbers of satisfied or unsatisfied parity check constraints; for example the criteria in [21] and the improved criterion in [22] compare the numbers of satisfied parity check constraints in two consecutive iterations. If they are equal, the decoding process is halted. On the other hand, the criteria in [23, 24] use the number of unsatisfied parity check constraints to detect undecodable blocks.
4. Improved Hybrid Decoding Algorithm
In the HB decoding process, the decoding time of IT decoding for undecodable blocks becomes longer as the decoding iterates for Imax. Figure 1 shows the iteration histogram as a function of the missing amounts experienced for two variants of group sizes, including 49 and 169 tags. Imax is set to 50 and 200, respectively. It is explicit that as the number of missing tags increases, iteration for Imax starts to occur due to the existence of undecodable blocks. This can clearly be seen in the region where IT decoding has failed, for example when recovering more than 15 and 70 missing tags from a group of 49 and 169, respectively. Therefore, the taking into account of an early stopping criterion, which adaptively adjusts the number of decoding iterations, arises as an attractive solution to avoid unnecessary iterations and thus to save decoding time. Since the main advantage of HB decoding is to reduce GE complexity, the frequency of GE decoding usage should be as small as possible,
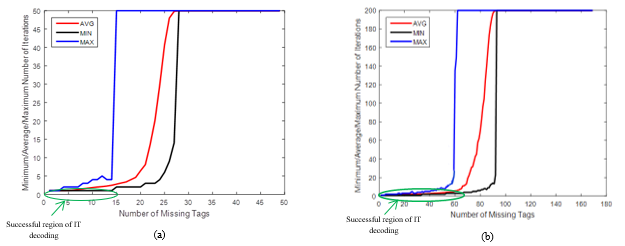
even for a large number of missing tags. When GE decoding is utilized, the size of the simplified system should also be as small as possible. This suggests a stopping criterion for the PEG-based method which permits partial decoding of undecodable blocks up to a point where IT decoding cannot recover any missing tag identifiers. The proposed criterion can distinguish between decodable and undecodable blocks. It does not cause any computation overheads, as it utilizes the information available during the decoding process. Algorithm 1 outlines the improved HB decoding algorithm. The input is the received codeword y = [y1, y2, … , yn] of the transmitted codeword x = [ x1, x2, … , xn] where xi ∈ {0,1} and yi ∈ {0, 1, e} for i = 1 … n. The output is M = [M1, … , Mn] where Mi ∈ {0, 1, e}. Let Sj denote the set of symbols in the j-th check equation of the code, ne is the number of erasures at the input to the decoder, and Ej,i is the outgoing message from the check node j to the variable node i. The improved algorithm is based on the observation of the checksum of erasure symbols at the end of each iteration I. It halts the decoding process if the checksum remains unchanged or does not decrease within two consecutive decoding iterations, as in Step 24. This results from the observation that decodable blocks exhibit a consistent decrease in checksum values. 

5. Simulation Results
This section gives an account of the various simulations which have been carried out to analyse and assess the performance of the PEG-based method under the improved HB decoding, both in terms of missing recovery capabilities and decoding complexities.
5.1. Missing Recovery Capability Analysis
To illustrate the performance of the improved HB decoding in recovering missing tags, Figure 2 shows the average error rate as a function of the number of missing tags for different values of group sizes n where the column weight j varies between 3 and 4. It can be clearly shown that increasing j greatly increases the performance of the improved HB decoding in recovering missing tags. The main reason for this behaviour is that a large value of j produces a large number of rows and thus increases the rank of the matrix. For example, if five tags are missing from a group of n = 25, all their identifiers can be recovered with at least j = 3 under the improved HB decoding. However, if ten identifiers are missing, the column weight needs to be adjusted to 4 in order to achieve 100% reliable recovery (0% error rate). Table 1 compares the missing recovery capabilities of the simulated PEG-based method under the improved HB decoding algorithm with other extended grouping methods presented in [2–4]. It is clear that the improved algorithm achieves significant missing recovery enhancements compared to other extended grouping methods. It can be concluded from the results that the improved HB decoding achieves the optimal missing recovery capabilities of full GE decoding, since the remaining systems of IT decoding containing short cycles are solved with GE decoding. The results also reveal that the recovery performance of the improved HB decoding increases by increasing the group size. This results from the fact that the PEG-based method accounts for short cycles in Tanner graphs by maximizing the local girth, i.e. the length of the shortest cycle, at variable nodes, which is more achievable when the group size is large [1]. Applying the improved HB decoding to groups of 25 and 49 tags, for example, results in the recovery of missing tags of up to 48% and 65%, respectively, of the group size, with a 0% error rate. On the other hand, for groups of 121 and 169 tags, the recovery capabilities increase to 72% and 74.5%, respectively.
5.2. Decoding Complexity Analysis
The relative complexities of the improved HB decoding are analysed in terms of decoding time. The decoding time is measured on a 2 GHz Intel i7 processor. The entire decoding complexity is equal to the complexity of IT decoding plus that of GE decoding if short cycles exist. This is mainly determined by the efficiency of the first stage of IT decoding; the better the performance of the IT decoding, the less the complexity and thus the time of the improved HB decoding. During the decoding process, IT decoding is first applied on the parity check matrix. If the IT decoding fails, GE decoding is activated to solve the remaining systems with a complexity less than the complexity of decoding the original matrix.
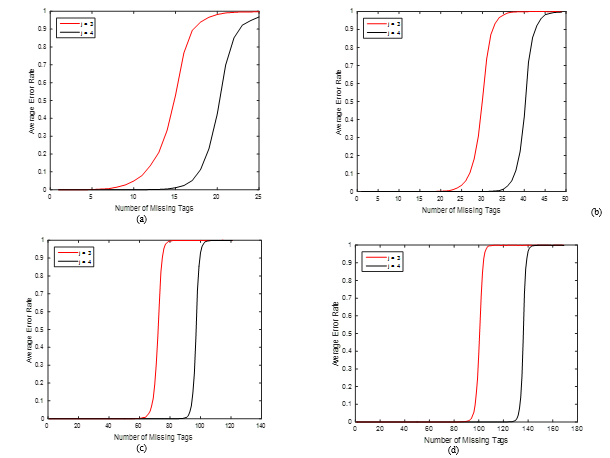
Table 1. Comparisons of missing recovery capabilities of the PEG-based method under the improved HB decoding algorithms with other extended grouping methods
| Parameter | Methods | Largest number of missing identifiers which can be recovered within 0% error rate | Parameter | Methods | Largest number of missing identifiers which can be recovered within 0% error rate |
| (25, 3, 5) | [2] | 3 | (121, 3, 5) | [2] | 1 |
| [3] | 5 | [3] | 5 | ||
| [4] | 5 | [4] | 5 | ||
| PEG-based method under GE decoding | 6 | PEG-based method under GE decoding | 64 | ||
| PEG-based method under HB decoding | 6 | PEG-based method under HB decoding | 64 | ||
| (25, 4, 5) | [2] | 5 | (121, 4, 5) | [2] | 6 |
| [3] | 7 | [3] | 13 | ||
| [4] | 9 | [4] | 15 | ||
| PEG-based method under GE decoding | 12 | PEG-based method under GE decoding | 87 | ||
| PEG-based method under HB decoding | 12 | PEG-based method under HB decoding | 87 | ||
| (49, 3, 5) | [2] | 1 | (169, 3, 5) | [2] | 1 |
| [3] | 5 | [3] | 5 | ||
| [4] | 5 | [4] | 5 | ||
| PEG-based method under GE decoding | 23 | PEG-based method under GE decoding | 93 | ||
| PEG-based method under HB decoding | 23 | PEG-based method under HB decoding | 93 | ||
| (49, 4, 5) | [2] | 3 | (169, 4, 5) | [2] | 1 |
| [3] | 7 | [3] | 9 | ||
| [4] | 8 | [4] | 16 | ||
| PEG-based method under GE decoding | 32 | PEG-based method under GE decoding | 126 | ||
| PEG-based method under HB decoding | 32 | PEG-based method under HB decoding | 126 |
Two experiments are conducted:
- Decoding time measurements when IT decoding fails and thus GE is required. This is the worst case from a decoding point of view.
- Decoding time measurements as a function of the number of missing tags to compare two cases, one where IT decoding is successful and the other where IT decoding fails and GE is needed.
5.2.1. Decoding Time when Gaussian Elimination is Required (Worst Case)
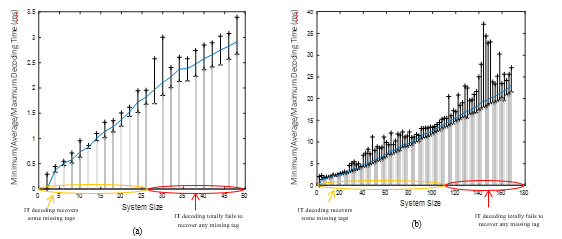
Figure 3 illustrates the decoding time during the GE process of the improved HB decoding for a group of 49 and 169 tags where j = 3. By changing the number of missing tags, the resulting average simplified system size changes, which affects the decoding time. The figure illustrates this time as a function of the simplified system size and the related histogram. The region where IT decoding recovers some missing tag identifiers is only considered in this analysis. However, in the second region, where IT decoding cannot recover any missing tag identifiers, GE decoding time is equal to that of full systems. The improved algorithm efficiently decreases the average decoding time of GE decoding, because the complex GE decoding is only utilized when required over a simplified system resulting from IT decoding. For a group of 49 tags, the histogram demonstrates that the maximum decoding time remains below 2 ms related to an average decoding time of 1.8 ms. When the group size increases to 169 tags, the GE decoding time also increases, following a O(n3) law. It can clearly be seen that the maximum decoding time remains below 13 ms related to an average decoding time around 12 ms. In contrast, GE decoding on full systems, as illustrated in Figures 5 and 6 (presented in the next section), is slower, especially for a large group of tags. For a group of size 49 and 169 where j = 3, it is evident that the decoding time lasts on average 2 and 15 ms, respectively.
To illustrate the impact of the proposed early stopping criterion on decoding time, Figure 4 shows iteration numbers which are taken for various missing amounts to be compared to those of the conventional IT decoding depicted in Figure 1. One can observe that the proposed stopping criterion greatly reduces the average number of iterations in the region where IT decoding is not successful. Figure 4 shows that undecodable blocks need at most 17 and 33 iterations, respectively, when recovering more than 15 and 70 missing tags from a group of 49 and 169.
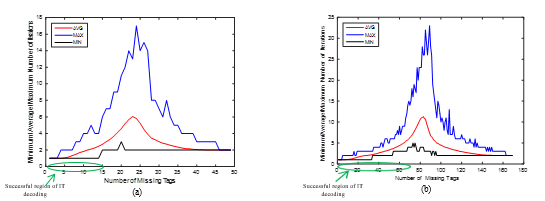
5.2.2. Decoding Time of the Improved Hybrid Decoding
Figures 5 and 6 show the average decoding time as a function of the number of missing tags for different values of n where j is equal to 3 and 4 under the IT, GE and improved HB decoding algorithms. It is obvious that the decoding time depends on the missing amounts experienced. With small numbers of missing tags, the decoding time of the improved HB decoding is fast and is similar to that of IT decoding. This is clear in a region where IT decoding is successful. As the number of missing tags increases, the decoding time of the improved HB decoding also progressively increases, because GE decoding is more and more often required. This can be seen in the curves: after the successful region of IT decoding, the average decoding time of HB decoding increases progressively, since IT decoding turns out to be ineffective, and the size of the simplified system increases accordingly. Then, above a certain threshold which depends on the missing recovery capabilities of IT decoding, the decoding time of the improved HB decoding gradually approaches the full GE decoding. Since the entire decoding time of the improved HB decoding is equal to the decoding time of IT decoding plus that of GE decoding, the improved HB decoding algorithm can easily be tailored to satisfy operational requirements. More precisely, the IT decoding phase can be avoided when the aforementioned condition is met, to save HB decoding time. It is clear that the n and j parameters also have major impacts on the decoding time. As n or j increase, the improved HB decoding time increases too. This is due to specific phenomena. The complexity of IT decoding depends on the number of XOR operations, which is determined by the number of variables in each equation, whereas the complexity of the GE decoding depends on the number of linear equations and the number of variables. Therefore, by increasing n or j, the number of operations required by the IT and GE decoding algorithms is increased accordingly. If decoding time is an issue with a large n value, choosing a smaller j value is possible. If the HB decoding time is compared with the GE decoding time for
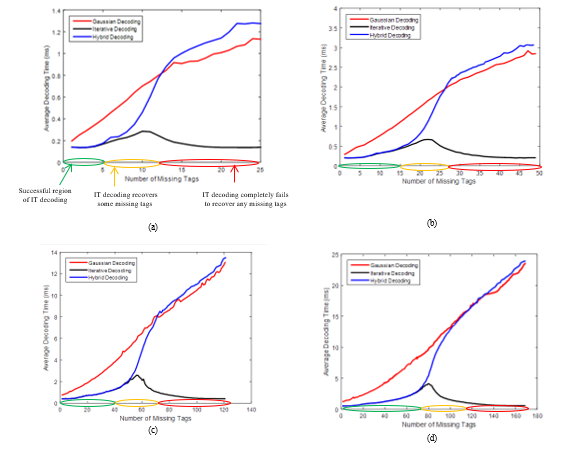
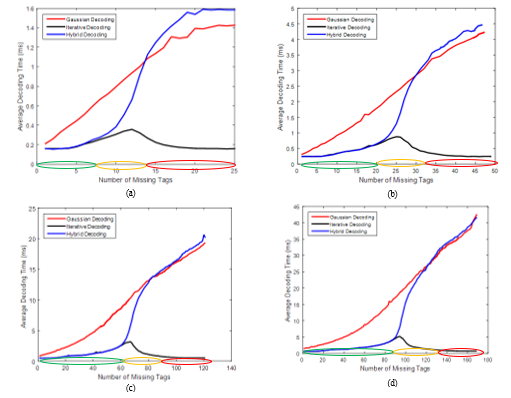
the full system, it can be concluded that the HB decoding is faster for small to medium numbers of missing tags even when GE decoding is required.
6. Conclusions and Future Work
This paper has focused on optimizing the decoding complexity of the PEG-based method using a hybrid iterative/Gaussian elimination decoding algorithm. The hybrid decoding is improved by including an early stopping criterion to avoid unnecessary iterations of iterative decoding for undecodable blocks and thus saving decoding time. Simulation results have been presented showing that the improved hybrid decoding algorithm achieves the optimal missing recovery capabilities of full Gaussian elimination decoding, since the remaining systems of iterative decoding containing short cycles are solved with Gaussian elimination decoding. This recovery performance significantly increases with an increase in the group size of tags. It has been shown that the proposed stopping criterion greatly reduces the average number of decoding iterations for undecodable blocks and therefore reduces decoding time when compared to the conventional IT decoding algorithm. The improved algorithm is very efficient in decreasing the average decoding time of Gaussian elimination decoding for small to medium amounts of missing tags up to a certain threshold which depends on the missing recovery capabilities of IT decoding. This makes the improved hybrid decoding a promising candidate for decoding the PEG-based method for extended the grouping of RFID tags.
For future work, more investigation is needed into the joint use of the two decoding algorithms according to missing amounts and group sizes.
- R. Alkanhel, M. Ambroze, “Extended Grouping of RFID Tags Based on Progressive Edge-Growth Methods” in 5th International Conference on Electronic Devices, Systems and Applications (ICEDSA), Ras Al Khaimah, UAE, 2016.
- Y. Sato, Y. Igarashi, J. Mitsugi, O. Nakamura, J. Murai, “Identification of Missing Objects with Group Coding of RF Tags” in 2012 IEEE International Conference on RFID, Orlando, USA, 95–101, 2012.
- Y. Su, J. Lin, and O. K. Tonguz, “Grouping of RFID tags via strongly selective families” IEEE Commun. Lett., 17(2), 1–4, 2013.
- Y. Su, O. K. Tonguz, “Using the Chinese remainder theorem for the grouping of RFID tags,” IEEE Trans. Commun., 61(11), 4741–4753, 2013.
- G. Liva, B. Matuz, E. Paolni, M. Chiani, “Achieving a near-optimum erasure correction performance with low-complexity LDPC Codes” Int. J. Satell. Commun. N., 28(5–6), 291–315, 2010.
- R. Gallager, “Low density parity check codes,” IEEE Trans. Inf. Theory, 8(1), 21–28, 1962.
- T. Richardson, R. Urbanke, “Efficient encoding of low-density parity-check codes” IEEE Trans. Commun., 47(2), 638–656, 2001.
- M. Cunche, V. Roca, “Improving the decoding of LDPC codes for the packet erasure channel with a hybrid Zyablov iterative decoding/Gaussian elimination scheme” INRIA Research Report, 1–19, 2008.
- M. Cunche, V. Roca, “Optimizing the Error Recovery Capabilities of LDPC-Staircase Codes Featuring a Gaussian Elimination Decoding Scheme” in 10th IEEE International Workshop on Signal Processing for Space Communications (SPSC), Rhodes Island, Greece, 2008.
- E. Paolini, G. Liva, B. Matuz, M. Chiani, “Generalized IRA erasure correcting codes for hybrid iterative/maximum likelihood decoding” IEEE Commun. Lett., 12(6), 450–452, 2008.
- L. Yang, M. Ambroze, M. Tomlinson, “Decoding turbo Gallager codes for the erasure channel” IEEE Commun. Lett., 1(2), 1–3, 2008.
- W. Huang, S. Member, H. Li, J. Dill, “Fountain Codes with Message Passing and Maximum Likelihood Decoding over Erasure Channels” in IEEE Wireless Telecommunication Symposium, New York City, USA, 1–5, 2011.
- M. Cunche, V. Saviny, V. Roca, “Analysis of Quasi-Cyclic LDPC codes under ML Decoding over the Erasure Channel” in IEEE International Symposium on Information Theory and its Applications (ISITA), Taichung, Taiwan, 2010.
- W. Ryan, S. Lin, Channel Codes Classical and Modern, Cambridge University Press, 2009.
- M. Luby, M. Mitzenmacher, M. Shokrollahi, D. Spielman, “Efficient erasure correcting codes” IEEE Trans. Inf. Theory, 47(2), 569–584, 2001.
- T. Xia, H. Wu, H. Jiang, “New stopping criterion for fast low-density parity-check decoders” IEEE Commun. Lett., 18(10), 1679–1682, 2014.
- F. Kienle, N. Wehn, “Low Complexity Stopping Criterion for LDPC Code Decoders” in 61st IEEE Vehicular Technology Conference, Stockholm, Sweden, 25–28, 2005.
- J. Li, X. You, J. Li, “Early stopping for LDPC decoding: convergence of mean magnitude (CMM)” IEEE Commun. Lett., 10(9), 667–669, 2006.
- Z. Cai, J. Hao, L. Wang, “An Efficient Early Stopping Scheme for LDPC Decoding” in 13th NASA Symposium on VLSI Design, Post Falls, Idaho, 1325–1329, 2008.
- T. Chen, “An Early Stopping Criterion for LDPC Decoding Based on Average Weighted Reliability Measure” in Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, Harbin, China, 123–126, 2012.
- D. Shin, K. Heo, S. Oh, J. Ha, “A Stopping Criterion for Low-Density Parity-Check Codes” in 65th IEEE Vehicular Technology Conference, Dublin, Ireland, 1529–1533, 2007.
- D. Alleyne, J. Sodha, “On Stopping Criteria for Low-Density Parity-Check Codes” in 6th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Graz, Austria, 633–637, 2008.
- G. Han, X. Liu, “A unified early stopping criterion for binary and nonbinary LDPC codes based on check-sum variation patterns” IEEE Commun. Lett., 14(11), 1053–1055, 2010.
- T. Mohsenin, H. Shirani-Mehr, B. Baas, “Low Power LDPC Decoder with Efficient Stopping Scheme for Undecodable Blocks” in IEEE International Symposium on Circuits and Systems, Rio de Janeiro, Brazil, 1780–1783, 2011.
Citations by Dimensions
Citations by PlumX
Google Scholar
Scopus
Crossref Citations
- Reem Alkanhel, Marcel Adrian Ambroze, "Decoding complexity analyses of PEG-based methods with the improved hybrid iterative/Gaussian elimination decoding algorithm." In 2017 International Conference on Electrical and Computing Technologies and Applications (ICECTA), pp. 1, 2017.
No. of Downloads Per Month
No. of Downloads Per Country
