1. Inroduction

To save resources (routers, optical fibers, etc.) networks should be efficiently designed. Diverse networks models were then defined and used to represent a wide range of issues in transportation, telecommunications, logistics, production and distribution networks. All these models consider a graph composed of nodes and edges (optical fibers, cables, etc). For a better use of these resources, networks designers should solve the modular Capacitated Network Design Problem (CNDP) which consists of selecting edges and allocating optimal capacities to route a set of commodities between source and destination pairs. Each edge of the graph has a potential set of module capacities with their associated costs, a fixed cost that is incurred only if the edge is selected, and a routing cost which is proportional to the amount of flows along the edge. Each commodity is defined by origin and destination nodes, and the amount of flow to be routed. The objective is to minimize three criteria: edge cost, modules and routing. These capacitated network design problems are NP-hard and very difficult to solve in practice. The CNDP is a particular case of the well known Multicommodity Network Design problem (MNDP), in which we distinguish an important number of special cases and extensions [1]. The most studied ones are:

• The unsplittable variant where the flow of eachcommodity is required to follow one route between the origin and the destination. This variant increases the difficulty of the problem [2].
• The expansion variant, where some edges al-ready have an existing capacity.
• The fixed charge MNDP [3][4] in which the linkcapacities are known. Solving MNDP consists to determine the set of edges that should be opened in the final topology.
• The capacitated MNDP, where the number ofmodules to install on the edges are modeled by integers [1]
• The Network Loading Problem (NLP), where thenumber of module types is limited, each one with a given unit cost and capacity.

Various heuristics and exact approaches have been developed for designing capacitated networks. However, the heuristic approaches are more likely to be trapped in local optima, while the exact approaches are applied only to small or medium size problems. Due to the weaknesses of the two approaches and the increasing popularity of metaheuristic approaches, we have witnessed many metaheuristics being applied to network optimization problems. In this paper, we propose a novel metaheuristic that combines linear programming with Genetic Algorithms (GAs) to solve

the CNDP problem. We recall that the genetic algorithms were extensively used to solve many difficult combinatorial optimization problems in industrial engineering and operation research. Genetic algorithms are one of the most powerful and broadly applicable stochastic search and optimization technique. They have achieved great advancement in related research fields, such as network optimization, combinatorial optimization, multi-objective optimization, etc. Our contribution consists in an efficient two steps-based heuristic that extends the approach in [5] by combining the GAs and Linear Programming (LP) to solve CNDP.

The remainder of this paper is structured as follows: related work is introduced in section 2, notations and mathematical formulation of the addressed problem are given in section 3. Section 4 describes and explains in details our proposed heuristic. Experimental results are discussed in section 5 where we compare our proposition against Iterative Local Search (ILS) algorithm. Finally, section 6 concludes the paper.

2. Related work

Capacitated Network Design Problem is one of the major research area in network optimization. It is related to two issues: Network Design Problem (NDP) and Network Loading Problem (NLP). In the NDP, the goal is to identify the network topology by selecting routers and links that interconnect them. Thus, the objective function aims to minimize the total constructive cost under some topological constraints. In this class of problems, the flow is not modeled and considered as uncapacitated. In the NLP, it is assumed that the topology is already established. Thus, solving NLP consists to search for the set of resources to allocate for the network components. These problems are complementary. Generally, NDP and NLP are solved separately though they should be combined together to optimize the resources.

One can say that most of network optimization problems can be seen as a kind of (1) NDP, (2) NLP or (3) a combination of both where the objective and the constraints may differ from one problem to another: connectivity [6] [7], limited budget [8], hop limit [2] [9], delay [10] [11], reliability [9] [10], and survivability [11]. The NLP in capacitated or uncapacitated case and with both single or multiple facilities is a special case of the well known Multicommodity Network Design Problem (MCND). Previous works on this problem can be classified as:

• Uncapacitated network design problems whereon each network link, it is only possible either to open the link with an infinite capacity and a given fixed cost, or the capacity and cost are nil

[12].

• Single facility capacitated network loading problem where, the capacity can be done by installing on each link an integer unit of a given basic facility [13].
• Two facilities capacitated network loading prob-lems where the capacity can be achieved by means of two types of modules, each capacity has a specific cost [14].
• Multi-type facility capacitated network loadingproblems where various types of capacities can be installed on each link, each facility has a specific cost [8].

The early works on capacitated modular network problems were focused on the approximation methods. These methods define residual capacity and cutset inequalities for single commodity and multicommodity cases on directed, undirected and bidirected link models [15][16]. Since these works consider that the underling network is established, they focus only on the determination of the facilities allowing the accommodations of flow demand. Their effectiveness depends on the size of the problem instance. With the appearance of metaheuristics, both the NLP and the NDP have attracted some attention. The authors benefit from their efficiency to deal with more complex variants with real size instances. In [17], the author compared several neighborhood structures to solve the uncapacitated facility location problem. In [11], the authors proposed an evolutionary approach for capacitated network design considering cost, performances and survivability. The objective is to minimize network cost and packet delay. Kleeman et al. [10] used an evolutionary algorithm to solve multicommodity capacitated network design problem with an objective function optimizing costs, delay, robustness, invulnerability and reliability. A tabu search heuristic algorithm with real costs on facilities is developed in [18]. A firefly algorithm is proposed by Ragheb et al [8], they combined facility location and network design problem with multi-type of capacitated link and limited budget on facilities. Contreras et al. [19] presented a unified framework of general network design problems which combine location decision and network design decision.

3. Mathematical Formulation

Let G = (V ,E) be an undirected network where V is the set of vertices and E is the set of undirected edges. Let K be the set of commodities. Each one k ∈ K is associated with a flow demand d_k and has a source denoted by the function s(k) and a target t(k). Let f_ij be the fixed cost of including edge (i,j) in the network, r_ij the unit variable flow cost on (i,j), and p_ij the preinstalled capacity on the edge (i,j).

The formulation of CNDP is shown below: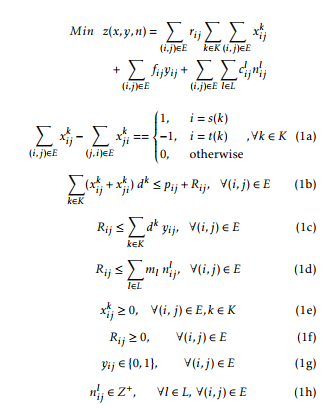

This formulation is a mixed integer linear program which uses four types of variables: the first type is a binary design variable y_ij which is defined as y_ij = 1 if (i,j) is included in the network and y_ij = 0 otherwise. The second type is a continuous path flow variable x_ij^k , which represents the amount of flow of commodity k routed on link (i, j). The third type is an integer allocation module variable n^l_ij which represents the number of module type l ∈ L (L is the set of potential modules) that should be allocated on edge (i, j). Each module l is characterized by a capacity m_l and an installation cost c_ij^l . The fourth type is a continuous variable R_ij representing the required flow capacity on link (i, j). A positive capacity p_ij + R_ij on edge (i, j) implies that it is used to route demands in the two directions: from i to j or from j to i. This formulation corresponds to a general model that can deal with several variants of capacitated network design problems.

The objective function corresponds to the sum of the flow costs, the fixed costs of edges and the allocated module costs. These costs are relative to the problem that we deal with and are not all aggregated in some cases. For instance, the fixed charge problem MNDP includes only the edge costs. The modules and routing costs on edges are nil. Constraints (1a) consist of flow conservation equations, for each commodity k. Constraints (1b) specifies that the required capacity R_ij on each link (i, j) should be greater than the cumulated flows traversing the link minus the preinstalled capacity. Constraints (1c) forces the installation of link (i, j) (i.e, y_ij = 1) if the required capacity R_ij is positive (otherwise, y_ij = 0). Constraints (1d) specify that the total capacity of the allocated modules should be greater or equal to the required capacity on each link. (1e) and (1f) state out non-negativity constraints for the decision variables X and R. Constraints (1g) express the binary nature of the variables Y whereas constraints (1h) show that the module facility are allocated in discrete amounts.

If we assume that the edge and module vectors (y,n) are fixed and known, the main task in the above formulation becomes the search of a feasible flow that satisfies all the demands with the use of limited and fixed link capacities. Hence, the NP-hard CNDP problem can be reduced to the Capacitated Multicommodity Flow Problem (CMFP) which is solvable in polynomial time and formulated as follows: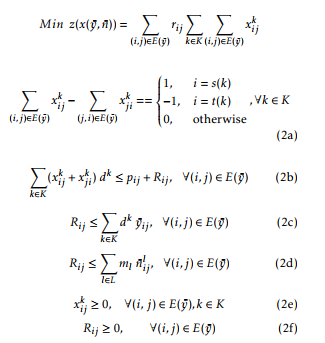

The multicommodity flow problem formulation presented in the linear programming (2) is obtained by replacing the vectors (y,n) in the original CNDP formulation (1) by their fixed values (y,¯ n¯). In this reformulation, the objective function aims to minimise the routing of flows. Constraints (2a) are flow conservation equations. For simplicity and efficiency, we delete the variables R by replacing the constraints (2b), (2c), (2d) and (2f) by the following constraints (3a):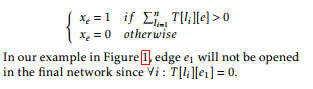

The previous constraints (3a) force the use of limited capacities by guaranteeing that the flows do not exceed the installed capacity (i.e, sum of the pre-installed capacity and module capacities). Constraints (2e) state out continuity and non-negativity of the decision variables X.

A solution to the CNDP can be viewed as (1) a binary assignment (y¯) to each design variable, (2) an integer vector assignment (n¯) to the allocation module design variables and (3) an optimal solution for the multicommodity minimum cost flow problem x^∗(y,¯ n¯). In this way, the CNDP objective function value associated to a solution (y,¯ n,x¯ ^∗(y,¯ n¯)) is the sum of the fixed cost of the open edges in (y¯), the cost of the modules allocated (n¯) and the objective function value of the CMFP associated to x(y,¯ n¯)^∗. Thus, to solve the CNDP problem, we propose here to separate it into two subproblems:

• link and resource selection which consists to choose the links, modules and their numbers by making decision on the vectors y and n,
• solve the CMFP problem (formulated in (2)) with respect of decisions made in (1) to determine the optimal routing that flows all the demands.

Note that sub-problem (2) can be solved in polynomial time. Thus, the challenge consists to solve the sub-problem (1) by identifying the best decision vectors (y) and (n) which allow to solve the flow subproblem in (1). In other words, the decision vectors (y) and (n) should be selected so that the overall routing, link and module costs are optimal.

In the next section, we show how to solve jointly and efficiently sub-problems (1) and (2). In the first step of our proposition, we used the genetic algorithms to explore different potential solution areas for the decision vectors (y,n). Each solution (y,¯ n¯) is then evaluated in the second step by solving CMFP problem.

4. Genetic Algorithm for CNDP

Genetic algorithms introduced by Goldberg et al. [20], are based on the mechanics of natural selection and genetic. They start with an initial set of random solutions, called a population. Each individual in the population, called a chromosome, represents a solution to the problem. The initial population evolves through successive iterations, called generations. A measure of fitness defines the quality of an individual chromosome. In each generation, chromosomes are evaluated by a fitness function, also called an evaluation function. After a number of generations, highly fit individuals, which are analogous to good solutions to a given problem, will emerge. Genetic algorithms consist of five components:

1. A method for encoding potential solutions intochromosomes;
2. A means of creating the initial population;
3. An evaluation function that can measure the fitness of chromosomes;
4. Genetic operators that can create the next generation population;
5. A way to set up control parameters; e.g., population size, the probability of applying a genetic operator, etc.

4.1        Individual representation

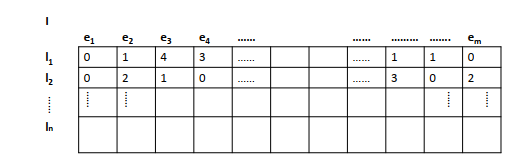
In the design of genetic algorithms, the encoding is the most important task. There are some methods to encode each individual in a population, such as binary encoding, integer encoding, etc. In this paper, we define a new encoding method called IME (Implicit Modular Encoding) that is relative to our modular case. An individual built by IME is shown in Figure 1. Each individual I is a matrix I_n,m, where n and m corresponds to the number of modules and to the number of edges respectively. Hence, I[l_i][e_j] gives the number of module types l_i allocated on edge e_j.

Our encoding represents the decision vector n and implicitly the decision vector y. For example, T [l₁][e₄] = 2 (see Figure 1) means that we should allocate two modules on the edge e₄. Thus, we implicitly deduce that edge e₄ exists in the final topology. When multiple types of modules are allowed, the edge exists if at least one module is allocated on it, i.e:

( xe = 1 if Pnli=1 T [li][e] > 0 x_e = 0 otherwise

In our example in Figure 1, edge e₁ will not be opened in the final network since ∀i : T [l_i][e₁] = 0.

4.2        Initial population

The choice of the initial population is a very important aspect of the whole search procedure. If it is too specific, then the search will be limited to a small region of the solution space leading to a local optimum. On the other hand, if the initial population is very

diverse then the algorithm will spend valuable computational resources exploring a variety of promising areas of the search space.

There are two ways to generate an initial population: random initialization and heuristic initialization. Here, we applied the Iterative Local Search (ILS) heuristic [21] that provides one approximated solution for the CNDP problem. To create a diverse initial population (c.f. algorithm depicted in Figure 2), we applied various perturbations on the individuals. After encoding the solution given by ILS heuristic according to IME, we obtain the first individual I₀. To form the rest of the initial population, we apply some perturbations on I₀. This results in the creation of new individuals,

wherein there are some ones corresponding to unfeasible solutions. Obviously, only individuals corresponding to feasible solutions are added to the initial population. We recall that an individual corresponds to a feasible solution to CNDP problem if its decision vectors n¯ and y¯ allow the flowing of all the demands. Thus, an individual corresponds to a feasible solution (n¯, y¯) if the linear program in (2) has solutions. Otherwise, the individual corresponds to an unfeasible solution.

Creation of the initial population’s individuals columns represent the edges, and the rows represent the module types allocated on edges. At initial stage, our population contains only one individual I₀. The other Individuals in the initial population are determined by applying some perturbations on the individual I₀. A perturbation consists to delete one module from the I₀’s edges. The complete procedure of generating the initial population is described in the following steps:

• for each module type l_n ∈ L,

for each edge e from the set E

Problem Instance	|V |	|E|	|K|	Nbr	L	MCost	pij	rij
Atlanta	15	22	210	TF	1000, 4000	variant	yes	yes
France	25	45	300	SF	2500	fixed	no	no
Germany50	50	88	662	SF	40	variant	no	no

Table 1: The Instance Setting Parameters

• create a new individual I that corresponds to a copy of I₀,
• decrement the number of modules l_n on the edge e of individual I
• add the new individual to the population if itallows a feasible flow of demands.

4.3       Fitness function

The fitness function corresponds to the objective function of CNDP. It is computed as the sum of the allocated module costs, the fixed edge costs and the routing costs. Note that the first two costs are deduced from the individual representation whereas the routing costs are given by solving the CMFP linear program (2).

4.4       Genetic operators

The next populations are generated by applying the crossover and mutation operators described below.

4.4.1      Crossover

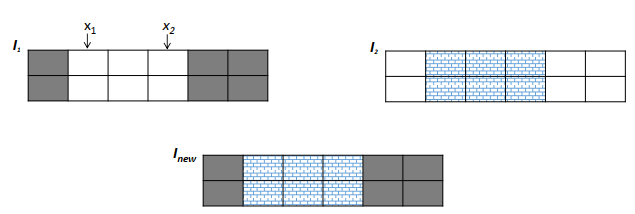
The crossover operator is responsible for combining two chromosomes so that a new offspring chromosome can be generated. In our proposition, we used a two point crossover: we randomly chose two integers in the individual length interval (0 < x₁ ≤ x₂ ≤ m) and two individuals (I₁ and I₂) in the current population, then we apply the two-point crossover operator to generate a new individual as shown in Figure 3. Typically, a new individual I_new is generated by selecting the modules of edges in (e₁,e_x1] ∪ [e_x2,e_m) from I₁ and (e_x1,e_x2) from I₂.

4.4.2      Mutation

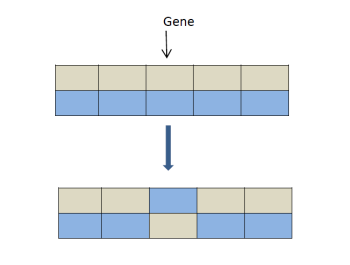
An edge (that corresponds to a gene) and two modules types are randomly chosen in the chromosome. Then, the numbers of modules relating to the selected types of modules are exchanged on the chosen edge (see Figure 4).

4.5       The genetic algorithm

After explaining and detailing the basic components of our proposed genetic algorithm, we describe below its operation (see Figure 5 for instructions). In our algorithm, we first initialize the population through InitialP opulation() procedure (see Figure 2). Then N successive populations are generated by applying the two-point crossover and mutation operators (Crossover() and Mutation()).

As said previously, only individuals allowing a feasible multicommodity flow solution are added to the current population. This is verified by the running of CplexSolver() procedure that solves the linear program in (2). The best solution Gbest is updated at each generation and returned when the termination condi-

 

Instance             BS                     ILS                   Gap%      GA                    Gap%

Atlanta               86492550      92904547      7.41          87959303      1.69

France                20200             21400             5.94         20600             1.98

Germany50       645520           719060           11.39       667840           3.45

Table 2: The ILS and GA solutions

Demand model	Undirected demand (U)
Link model	Undirected links (U)
Link capacity model	Modular link capacities(M)
Fixed-charge model	No fixed-charge cost (N)
Routing model	Continuous (C)
Admissible path model	All paths (A)
Hop limit model	No hop-limits (N)
Survivability model	No survivability (N)

Table 3: The model filter

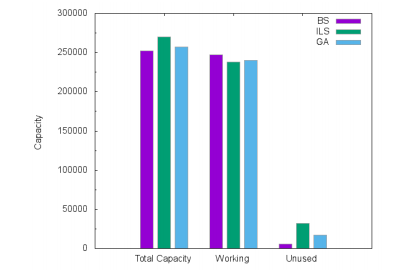
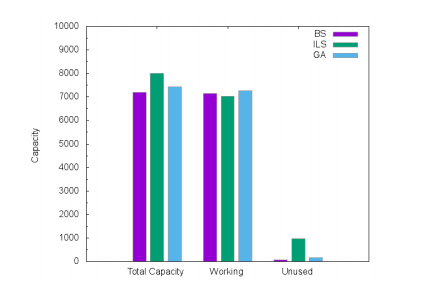
Table 4: Working and unused capacities

tion is satisfied.                                                                                  tion.

		Atlanta			France			Germany50
Instance	BS	ILS	GA	BS	ILS	GA	BS	ILS         GA
Total installed	294000	307000	300000	252500	270000	257500	7200	8000      7440
link capacities Total working flow	282338.5	281188	284503	246938	237952	240351	7140	7024         7265.83
Total Unused flow	11661.5	25812	15497	5562	32048	17149	60	976        174.17

5. Experiments and Results

In our experiments, we used three real world instances of network topologies including Atlanta, France and Germany50. All can be downloaded from http : //sndlib.zib.de [22]. We followed the model filter specified in Table 3. The population size is 50 and the number of generations is 15. Each instance is characterized by the number of nodes |V |, the number of potential links |E| = m and the number of traffic demands |K|. Table 1 summarizes the instance specification details. We classify them into two categories; instances with Single Facility allocation (SF) and instances with Two Facilities allocation (TF). The set of capacity modules L differs from one network instance to another. The allocation cost MCost is variant on links except in France instance. Atlanta instance assumes a Pre-installed capacities p_ij on their potential links with a unit routing cost r_ij. See [22], for more details on the filter model and on the setting parameters.

In Table 2, ILS and GA correspond to the solutions obtained by iterative local search algorithm and our genetic algorithms-based heuristic respectively. We examine the quality of a given algorithm A (A could be GA or ILS) by computing its optimality gap (see equality 10) that is defined as the ratio between the difference of the A’s cost and the Best Solution (BS) cost. Note that BS corresponds to the best solutions published in [22].

GAP (A) = {Cost(A) − Cost(BS)}/Cost(BS) ∗ 100          (4)

As depicted in Table 4, GA is better than ILS since it determines solutions more close to the best solutions than those of ILS. Concretely, the mean gap obtained with ILS is 3.5 times higher than the mean gap obtained with GA. This can be explained by the exploration of multiple solution areas with GA while ILS determines only a local optimum.

Figures 6, 7 and 8 show the allocated capacities and their usage for Atlanta, France and Germany50 networks respectively. We compared the total installed link capacities, the total working capacities and the total unused capacities for BS, ILS and GA solutions. We remark that the total installed link capacities in ILS and GA are more larger than the BS ones. This justifies the cost gap. On the other hand, ILS uses fewer working capacities than BS because ILS wastes and over-allocates module resources, leading to efficient routing. Indeed, instead of splitting flows and exploring the small unused capacities on links, ILS routes the majority of demands on shortest paths. With GA, the CPLEX optimizer tries to exploit the residual quantities on the allocated modules to route the flows. This leads to a bifurcation of demands on multiple paths that could be quite long, though routing costs slightly limit the path lengths.

6. Conclusion

In this paper, we proposed a two steps-based algorithm to solve the modular version of the Capacitated Network Design Problem (CNDP). In the first step, we applied genetic algorithms to select sets of promising networks (i.e., links with their modules) which are checked, evaluated and validated in the second step with the use of linear programming.

To explore the promising areas in the solution space, the genetic algorithms we used were adapted to treat and design efficient network topologies by: (1) defining a flexible and meaningful encoding scheme IME (Implicit Modular Encoding), (2) two point crossover and mutation operators and (3) an elitist population strategy. We generated the initial population by combining an iterative local search algorithm with a heuristic procedure that modifies the number of modules on the network links. Successive populations were then generated by applying two point crossover operator which creates a new network from two other ones by selecting some edges from the first network and the rest from the second network. A mutation operator is possibly applied on links to exchange the module types. Finally, a probabilitybased elitist population strategy chooses promising network topologies that we combine to determine the next population. In our proposition, the networks are associated with probabilities in a way they guarantee an offspring often coming from the best individuals.

To measure the fitness of a solution, polynomial time linear program which determines the routes by searching for feasible flows on the corresponding network is used.

Simulations results confirm that the combination of genetic algorithms and linear programming in two steps is satisfactory and efficient. Indeed, the results show clearly that our proposition outperforms the iterative local search heuristic and determines solutions close to the known best ones.

1. A. Frangioni and B. Gendron, “0-1 reformulations of the multicommodity capacitated network design problem,” Discrete Applied Mathematics, vol. 157, no. 6, pp. 1229 – 1241, 2009.
2. B. Thiongane, J.-F. Cordeau, and B. Gendron, “Formulations for the nonbifurcated hopconstrained multicommodity capacitated fixed-charge network design problem,” Computers & Operations Research, vol. 53, no. 0, pp. 1 – 8, 2015.
3. I. Rodriguez-Martin and J. J. Salazar-Gonzalez, “A local branching heuristic for the capacitated fixed-charge network design problem,” Computers & Operations Research, vol. 37, no. 3, pp. 575–581, 2010.
4. D. C. Paraskevopoulos, T. Bektas¸, T. G. Crainic, and C. N. Potts, A Cycle-Based Evolutionary Algorithm for the Fixed-Charge Capacitated MultiCommodity Network Design Problem. Tech. rep., Centre interuniversitaire de recherche sur les reseaux d’entreprise, la logistique et le transport, ´ Montreal, 2013.
5. M. Khelifi, S. Boudjit, and M. Y. Saidi, “Two level evolutionary algorithm for capacitated network design problem,” in 13th IEEE Annual Consumer Communications & Networking Conference, CCNC16, Las Vegas, NV, USA, January 2016, pp. 299–300.
6. A. Balakrishnan, M. Banciu, K. Glowacka, and P. Mirchandani, “Hierarchical approach for survivable network design,” European Journal of Operational Research, vol. 225, no. 2, pp. 223–235, 2013.
7. M. Abd-El-Barr, “Topological network design: A survey,” Journal of Network and Computer Applications, vol. 32, no. 3, pp. 501 – 509, 2009.
8. R. Rahmaniani and A. Ghaderi, “A combined facility location and network design problem with multi-type of capacitated links,” Applied Mathematical Modelling, vol. 37, no. 9, pp. 6400–6414, 2013.
9. T. Liu, W. Yang, and J. Huang, “Reliable network design problem under node failure with benders decomposition,” Applied Mathematics, vol. 5, p. 241, 2014.
10. M. Kleeman, G. Lamont, K. Hopkinson, and S. Graham, “Solving multicommodity capacitated network design problems using a multiobjective evolutionary algorithm,” in IEEE Symposium on Computational Intelligence in Security and Defense Applications, 2007, pp. 33–41.
11. A. Konak and A. Smith, “Capacitated network design considering survivability: an evolutionary approach,” Engineering Optimization, vol. 36, no. 2, pp. 189–205, 2004.
12. T. Magnanti, P. Mireault, and R. Wong, Tailoring Benders decomposition for uncapacitated network design. Springer, 1986.
13. F. Barahona, “Network design using cut inequalities,” SIAM Journal on optimization, vol. 6, no. 3, pp. 823–837, 1996.
14. H. Kerivin, D. Nace, and T.-T.-L. Pham, “Design of capacitated survivable networks with a single facility,” IEEE/ACM Trans. Netw., vol. 13, no. 2, pp. 248–261, 2005.
15. A. Atamturk, “On capacitated network design cut–set polyhedra,” Mathematical Programming, vol. 92, no. 3, pp. 425–437, 2002.
16. A. Atamturk and D. Rajan, “On splittable and unsplittable flow capacitated network design arc–set polyhedra,” Mathematical Programming, vol. 92, no. 2, pp. 315–333, 2002.
17. D. Ghosh, “Neighborhood search heuristics for the uncapacitated facility location problem,” European Journal of Operational Research, vol. 150, no. 1, pp. 150–162, 2003.
18. O. Brun, J. Garcia et al., “A tabu search heuristic for capacitated network design,” in IEEE Symposium on Computers and Communications,ISCC, 2009, pp. 461–467.
19. I. Contreras and E. Fernandez, “General network ´ design: A unified view of combined location and network design problems,” European Journal of Operational Research, vol. 219, no. 3, pp. 680– 697, 2012.
20. D. E. Goldberg and J. H. Holland, “Genetic algorithms and machine learning,” Machine learning, vol. 3, no. 2, pp. 95–99, 1988.
21. M. Khelifi, M. Babes, S. Ghanemi, M. Y. Saidi, and S. Boudjit, “Hybrid heuristic for capacitated network design problem,” J. High Speed Networks, vol. 21, no. 4, pp. 313–330, 2015.
22. S. Orlowski, R. Wessaly, M. Pioro, and A. Tomaszewski, “Sndlib 1.0 survivable network design library,” Networks, vol. 55, no. 3, pp. 276–286, 2010.

(Click to view)

(Click to view)