1. Introduction

Circuit networks have become more attractive in recent years because they can be employed for the modelling of both electrical and non electrical systems, such as biological and chemical ones [1,2]. A study on resistance networks of graphine which indicates the existence of the planar circuit networks in nature won the 2010 Nobel Prize in Physics [3-5]. Over the past few decades, researchers have published some papers on the integer circuits networks. However, the last efforts have been focused mainly on analyzing the resistors or capacitors of the fractional order single component circuit networks [6,7]. Comparatively little attention has been paid to the impedance of the fractional-order multiple- component circuit networks.

Fractional-order mathematical models developed for inductors and capacitors could describe the electrical characteristics more accurately, which allows for higher flexibility, more freedom, best fit and better optimization techniques. In other words, the actual inductors and capacitors are fractional-order in nature [8]. Fractional-order inductors could be designed based on skin effect. Moreover, the fractional order capacitors  have been created with different electrolytes  recently [9-11].

Nowadays some researchers have been studying to design and realize the fractional elements [12-16]. Furthermore, some researchers have also concentrated on the study of fractional-order circuit theory [17-20]. However, only few researchers are interested in the electrical characteristics of 2xn circuit networks in fractional-order sense. Therefore, we focus on impedances and transfer functions of the network in fractional domain.

The following research contents could make our research more attractive. Firstly, network transfer function and equivalent input impedance formula are obtained depending on cell numbers used in network and fractional-order values. Cascade connection method with the  transmission matrices is developed for this derivation. Secondly, the characteristics of circuit network impedance and the transfer function are investigated  with respect to cell numbers and fractional-order values by means of MATLAB simulation programs.

 2.       Analysis of Fractional-Order 2xn RLC Circuit Network
Figure 1 represents the diagram of the fractional-order 2xn RLC circuit network, where z₀ refers to the resistors, z refers to the fractional order capacitors, and z₁ refers to the fractional-order inductors [17]. The represented network model is planar, and contains only passive circuit elements.                             

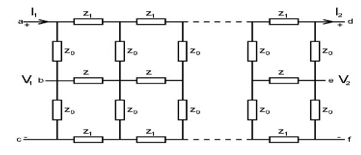
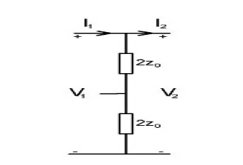
In order to obtain equivalent impedance and transfer function formula of the fractional-order circuit network, the basic circuit network theory, the two-port transmission matrix, and the matrix tranformation methods are employed. It is clearly seen that the circuit network model shown in Figure 1 includes the  network submodel shown in Figure 2a, and the network submodel shown in Figure 2b, which are connected  in cascaded form. One can easily verify that the whole circuit network is formed by cascading these submodels. With the help of the calculated transmission matrices for each submodel equivalent transmission matrix, the whole network model can be computed. From the equivalent transmission matrix, the transfer function and the equivalent impedance of the complete network can easily be found.

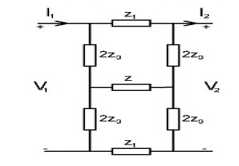
Transmission matrice for the two-port network shown in Figure 2a is calculated by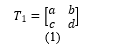

Where parameter values of the transmission matrice given by (1)  are defined respectively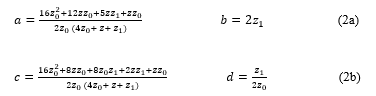                                                               

Transmission matrice for the two-port network shown in Figure 2b is computed by the following equation.                       

Transmission matrix for the whole network connected in cascaded form becomes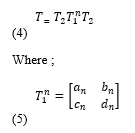

T₁ⁿ  is defined as nth power of T₁ matrice. From Cayley-Hamilton theorem, the following equation can be written as

Equivalent input impedance and transfer function can easily be obtained by means of  T transmission matrix given by (8). Equivalent input impedance and transfer function are given below, respectively.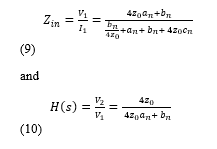

The derived equivalent input impedance and transfer function  equations are employed for the dynamic analysis of fractional-order 2xn circuit network. Finally, the analytical equations for the equivalent impedance and transfer functions are presented in the rational equation form. These equations vary with cell numbers and fractional-order values, thus dynamic characteristics of  the network can be investigated with respect to cell numbers and fractional-order values.

3. MATLAB Simulation of Network

The given example of the circuit network shown in Figure 1 with n=10 cell is simulated by using MATLAB program. Firstly, the equivalent input impedance and the transfer function of the circuit network are computed by means of symbolic programming in MATLAB. Then, by using the first order approximations presented in literature for the fractional elements, the transfer function and the equivalent input impedance are correspondingly obtained  in the rational function form. Finally, the characteristics of the transfer function and the equivalent input impedance of  the 2xn circuit network, such as frequency response, step and impulse responses are investigated with MATLAB simulations.

The parameter values of the proposed network in fractional domain are chosen as z₀ = 1, z₁=s^0.5, z=s^-0.5, n = 10, α = β = 0.5. In the simulation,  s^0.5=(3s+1)/(s+3) the first order approximation are used fort he fractional terms [14]. Firstly, frequency response, step and impulse responses of transfer function given by (10) are obtained by using MATLAB simulations. Graphics of these responses are shown in Figure 3a, 3b, 3c, respectively.

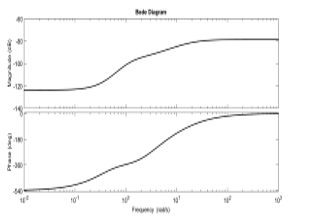
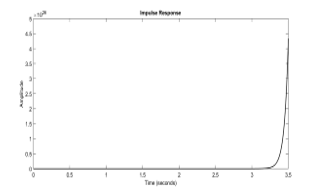
From the simulation results, we can conclude the following interpretations about transfer function of the network. It is clearly seen that the characteristics of the transfer function has high pass filter characteristic, and the transfer function is  stable.

Later, by using the same parameter values and the same approximations  for the equivalent input impedance defined in (9), the MATLAB simulations are repeated in fractional domain. Frequency response, step and impulse responses of equivalent input impedance corresponding results are shown  in Figure 4a, 4b, 4c., respectively.

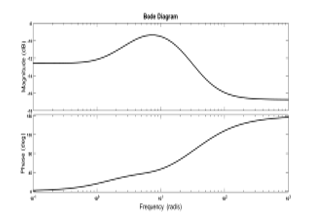
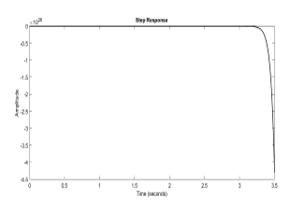
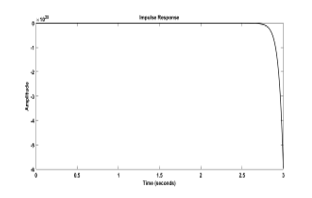
From the simulation results, the following interpretions about impedance function can be concluded. It is clearly seen that the characteristics of the equivalent input impedance function has low pass filter characteristic, and the impedance of the network is stable

4. Results and Conclusion

Mathematical model of the fractional- order 2xn RLC circuit network are developed  by means of  two-port transmission matrices in fractional domain. Mathematical model is in the form of fractional order rational function. By using rational function approximation for the each fractional-order term, the transfer function and the equivalent input impedance of the 2xn circuit network are presented in the form of rational transfer function. Although the fractional- order circuit network contains nonlinear elements, such as fractional- order inductors and capacitors, the transfer function approximation can be employed by using the Laplace transform properties. We have proposed a new method to model and to analyze the fractional- order circuit network in fractional domain.

The characteristics of the equivalent impedance and transfer functions of fractional-order circuit network are investigated by using the MATLAB simulation programming. Network characteristics, such as the frequency, step and impulse responses are obtained graphically for both equivalent impedance ant transfer functions. The dynamic stability and the characteristics of the fractional- order 2xn circuit network are also investigated with respect to the model parameters, such as cell numbers and fractional –order values.

1. Von Busse V, Swartz S. M., and C. C. Voigt C. C., “Flight metabolism in relation to speed in Chiroptera: Testing the U-shape paradigm in the short-tailed fruit bat Carollia perspicillata,” J. Exp. Biol.,. 216(11),. 2073–2080, 2013.
2. Simpson R., Jaques A., Nunez, C H.. Ramirez, and Almonacid A.,“Fractional calculus as a mathematical tool to improve the modeling of mass transfer phenomena in food,” Food Eng. Rev., 5(1), 45–55, 2013.
3. Bolotin K. I., Ghahari F., Shulman M. D., Stormer H. L., and Kim P.,“Observation of the fractional quantum Hall effect in graphene,” Nature, 475(7), 7354-7358,. 2011.
4. Feldman B. E., Krauss B., Smet J. H., and Yacoby A., “Unconventional sequence of fractional quantum hall states in suspended graphene,” Science, 337(6099), 1196–1199,. 2012.
5. Owaidat M. Q., Hijjawi R.S. and Khalifeh J.M.,” Network with two extra interstitial resistor”, Int. J. Theor. Phys., Vol: 10, 3152 – 3159, 2012.
6. Yao N. Y., Gorshkov A. V., Laumann C. R., Lauchli , J. Ye, and. Lukin M. D, “Realizing fractional Chern insulators in dipolar spin systems,” Phys. Rev. Lett., 110(18), 2013.
7. Hijjawi R.S., Assad J.H and Sakaji H.J, “Perturbation of an infinite network of identical capacitors”, Int. J. Mod. Phys., Vol: B2, 199 – 209, 2007.
8. Tripathy M. C. and Behara S.”Modelling andanalysis of fractional capacitors”, IJAS, Vol.2(10), 29-32, 2015.
9. Freeborn T. J.,”A survey of fractional order circuit models for Biology and Biomedicine”, IEEEJ in Circuits and Systems”, Vol.3(3), 2013
10. Westerlund S., “Dead Matter has Memory, Causal Consulting Kalmar”, Sweden, 2002.
11. Tenreiro M.J.A. and Galhano A.M.S.F.,” Fractional order inductive phenomena based on the skin effect”, Nonlinear Dyn., Vol: 1-2, 107 – 115, 2012.
12. Radwan A. G. and Salama K. N., “Passive and active elements using fractional L?,?α circuit”, IEEE T. Circuits-I, Vol: 10, 2388 – 2397, 2011.
13. Das S., Sivaramakrishna M.,. Biswas K and Goswami B., “Performance study of a constant phase angle based impedance sensor to detect milk adulteration, sensors and actuators”, A-Physical, Vol: 2, 273-278, 2011.
14. Krishna M.S., Das S., Biswas K and Goswami, B. “Fabrication of a fractional order capacitor with desired specifications; A study on process identification and characterization”, IEEE Trans. Electron Dev., Vol: 11, 4067 – 4073, 2011.
15. Haba T., Ablart G., Camps T. and Olivie F.,” Influence of the electrical parameters on the input impedance of a fractal structure realised on silicon”, Chaos Solitons Fract., Vol: 2, 479 – 490, 2005.
16. Elshurafa A.M., Almadhoun M.N., Salama K.N. and Alshareet H.N., “Microscale electrostatic fractional capacitors using reduced graphene oxide percolated polymer composites”, Appl. Phys. Lett., Vol: 23, 1234-1237, 2013.
17. RadwanA.G. and Salama K.N.,” Fractional – order RC and RL circuit”, Circuits Syst. Signal Process, Vol:6, 1901 – 1915, 2012.
18. Jia H.Y., Chen Z.Q. and.Qi G.Y, “Topological horsesshoe analysis and circuit realization for a fractional-order Lu system”, Nonlinear Dynam., Vol: 1 – 2, 203 – 212, 2013.
19. Chen P. and He S. B., “Analysis of the fractional-order parallel tank circuit”, J. Circuits sys. Comput., Vol: 6, 452-458, 2013.
20. Maundy B., Elwakil A.S. and Freeborn T.J,” On the practical realization of higher order filters with fractional stepping”, Signal Process, Vol: 3, 484 – 491, 2011.
21. Kuttler K, Linear Algebra , Ventus Publusing ApS, 2012

(Click to view)

(Click to view)