1. Introduction

UAV is a popular air reconnaissance platform due to developed technologies that it were allowed to use a large number of constructive elements and motion control components for its creation. Now developers of unmanned vehicles pay attention to air platforms with the possibility of vertical launch and landing and existence a programmable control such as a Quadrotors that were developed recently.

Compared with other types of UAVs the Quadrotor differs accuracy of positioning, fly stability, allowable flight time, payload, and reliability. Such platforms can not only carry a payload, but also fly a flexible program. Their main tasks can be ground surveillance, execution of search and rescue operations, fire detection, cargo operations and military tasks. The advantage of the UAV is a low cost operation, no pilot that rules out the risk of loss of human life, existence software for performance of variety problems.

Intuitively, we can assume that application of the group of UAVs is more effective than the application of one aircraft. As parameters of evaluation of the effectiveness of the group except for accuracy and time performance can be the number of assignments, objectivity and reliability of its performance. However, group behavior is more difficult than the behavior of one UAV.

An important task, as in the case of one UAV, is path planning of a group. This task complicated the flight safety requirement. The distance between UAVs should be neither small, nor very large in order to keep the integrity of the group. Usually minimum distance between elements of group must not less than 2-3 maximal length of aircraft. The requirement of flight safety is achieved by increasing the distance between the UAVs. Maximum distance must to accord stable communication between elements of group. Thus for maintaining the integrity of the group distance between agents should not be too large.

For solving main problems, the behavior of group used agent-based approach as usually. Tasks performance also should be provided by mechanisms and procedures of interaction for achieving common goal. The classic approach to solving this problem is the use in scientific works of methods based on the analogies with sociality in animals and especially in insect societies. However, not all of these methods are suitable for use in technical means, as a group of technical agents usually manages by human operator, the group consists of a limited number of UAVs, and it must operate in a real environment where there is interference and obstacles movement. Considering these properties increases the flow of data in the system, leads to an increase computational and technical complexity of a system.Group’s elements should know how to interact in order to achieve mission goal. To solve it, we consider methods that are based on behavior of herds of animals, birds and insects. Unfortunately, not all of them are suitable for application in technical means because it needs definition the man-operator role, group of UAVs should not be too large otherwise it technical and calculated complexity realization of this system will lead to expensive of managing system. Flight control of big UAVs team is need transmission the significant data flow and increasing time on decisions making.

In some cases, the performance of tasks limited interference of artificial or natural origin. Impact of power interference on the group flight leads to restructure of a group or change the route in order to achieve flight objectives. Thus, the interference signals should be known for synthesis of a control law.

The problem formulation involves the traditional description of group behavior as a dynamic system with restrictions on the intervals and the distance between the individual elements of the group. The group performs the movement on a route. There are fixed obstacles that located on the path of its movement. The mission of a group is to reach the goal and to avoid collision on the route.

In this paper considered movement of Quadrotors group that carry out monitoring of ground surface. Main problem of this task we consider the maintenance the group size for following of the route. Group consists of an agent-leader and agent-members that are fulfil their task in some closed region, where located an obstacles. One of problems that should be solved is to overcome an obstacles type of «bottleneck» on a route of UAVs.

The structure of this paper is organized as follows: in the next section, related work on the behavior of UAVs group is reviewed. Section 3 gives the system model and problem formulation. Section 4 provides movement stability study in different condition. The control laws for movement with and without obstacles are also proposed. Analysis of a Quadrotor model as a group element conducts in Section 5. Simulations conducts in Section 6. Section 7 concludes the paper.

2.       Related work

This paper is an extension of work originally presented in International Conference “Methods and Systems of Navigation and Motion Control (MSNMC)” [1], which considered a description of group dynamics UAV in the presence of fixed obstacles.

Despite the fact, that currently drawn a lot of reviews and publications on multi-agent systems, the most common questions about this type of systems given in [2]. This monograph introduces the concept of autonomous agents capable of performing independent activities. Generalized architecture of agent system has three levels of management that are answer for the planning, conduct and interaction of the system.

The results of the use of multi-agent systems when performing practical tasks is given in [3-6]. In [3], for example, using the principles of ant colony for wireless sensor networks and new routing functions is considered. The proposed algorithm of optimization synthesized by on a probabilistic procedure, whereby authors cannot reduce the amount of computational operations that occur during the delivery of information packets. The positive results obtained by the authors using known approaches based on search algorithms, evaporation and aggregation.

In [4] proposed algorithms coordination and optimization of multi-agent system RobotCup to perform rescue operations. Coordination of agents carried out on protocol that provided by some agreements and optimization by the way modified A* algorithm and search Nilsson’s algorithm. The work demonstrates the advantages of decentralized management for these tasks.

The authors [5] consider UAV swarm consisting of Quadrotors whose actions modeled by algorithms of behavior of animals and insects swarm. Conducted experiments revealed that quality of multi-agent system depends on the number of agents, but increases the number of links in the group, making it difficult to manage the system.

The problem of robot control and dynamic goal on surface coordinates is represented in [6]. Robot movement occurs in additive potential field of attractive and repulsive forces. These functions depend on mutual positions, velocities, and accelerators between robot and goal. If deviation of position, velocity and acceleration of the robot from the corresponding goal coordinates is equal to zero, robot is stopped.

Tracking the robots of a moving goal are presented in [6], [7]. The movement of vehicles [6] and UAVs swarm [7] occurs in the additive potential field forces of attraction and repulsion. The resulting force depends on the relative position, speed and acceleration, developed between robot and objective. Stopping robots is performed on speed and acceleration coordinates.

In [7] considered movement of swarm of UAVs for target tracking. The UAVs swarm moving to the target in artificial potential attractive and repulsive field. Attractive field will lead any free agent to the swarm. Repulsive field helps to avoid collisions and to save constant distance between the systems. Authors propose main ideas with respect to analytical relations for description of potential field.

The authors [8] introduced the concept of aggregation for movement and control operations of units with kinematic links. Agents described by integrators and transition to another positions performer in sliding mode. The main goal this movement lies in the avoidance of “unfavorable” positions on the way. Motion carried in potential field, which is a closed area some size. The disadvantage of this presentation is to use a large amplitude control signals which cause the sliding mode of agents, leading to at least to delay the process control.

The authors [9, 10] offer a description of the actions the group of agents for computer network. Agents’ actions are based on the protocol of negotiations between neighbors, according to them the agent network is created on principles of self-organization. To support cooperation agents and avoid delays in the process of organizing the authors suggest a mechanism of mutual concessions and the management on algorithm Q-learning.

In solving practical problems the most interesting is route planning. Recent results on the topic presented in [11-13]. The combination of advanced heuristic search algorithm A* and stochastic dynamic programming approach in planning the trajectory of an unmanned ground vehicle is proposed in [11]. To avoid the pits, ditches and congestion on the route, the unmanned vehicle uses information from optoelectronic sensors, which it is equipped, to optimize the route in real time.

Planning of the route with fixed wing of UAVs by using differential geometry solved in [12]. For carrying out the maneuver type of slew for a minimum time with constant velocity authors propose to build a route on well known Dubins path, arcs curves submitted semi-circles and segments of straight lines, but the lateral acceleration becomes intermittent. Continuousness of acceleration achieved using Pythagorean hodograph. In [13] authors solve a similar problem by Bezier curves.

For a stable and reliable work group is responsible communication subsystem. In [14, 15] addresses the problem of providing subsystem reliability data. Common approaches to the design of the subsystem presented in [14], especially that arising in data and algorithms for their consideration could be found in [15]. Planning methods trajectory shown in graph theory [16]. The motion work is carried out within the given trajectories. In this paper, movement is viewed as completely determined task at a constant speed and without interference.

Mission of path planning can be solved by methods of graph theory as shown in [16]. Robots are moving between spots of interest. Authors assume robot movement to determinate the order with the constant velocity and without obstacles.

An approach of tracking UAVs for the moving target is presented in [17]. The movement of a UAVs swarm occurs in attractive and repulsive fields that created regarding robot-leader by state feedback controller. However, Lyapunov criterion that is applied in the work, assumes stability only in the asymptotic behavior at large time interval, and it may not be applicable in the presence of obstacles.

The problem of surveillance by swarm of UAV of moving target given in [17]. Movement of swarm occurs in a potential field created robot’s controllers relatively leader by feedback. Proposed the Lyapunov criterion for evaluating the stability of motion has effect only on a large interval of a time, and it cannot used in presence of interference. Practical realization where robot follow to target with radio interference was given in [18]. Unfortunately, the proposed method is not suitable for controlling the UAV.

Compared to [1], in this work is developed synthesis UAV traffic control for a limited size group, which is not fixed and it can increase with rounding maneuvers and obstacles.

Compared to previous work, are proposed in this paper the algorithms of explicitly solution of the task moving in bounded conditions. The main algorithm creates two tasks. First task is to save dimension of the group when naturals or imitation obstacles of increase its dimension. Second task is to guarantee performance of the main task of group. To solve these tasks, much used potential field between robot-members within group and feedback control for following for robot-leader of group. Correctness of the proposed algorithm is proved. The details of the algorithms are presented in Section IV.

3.       Problem formulation

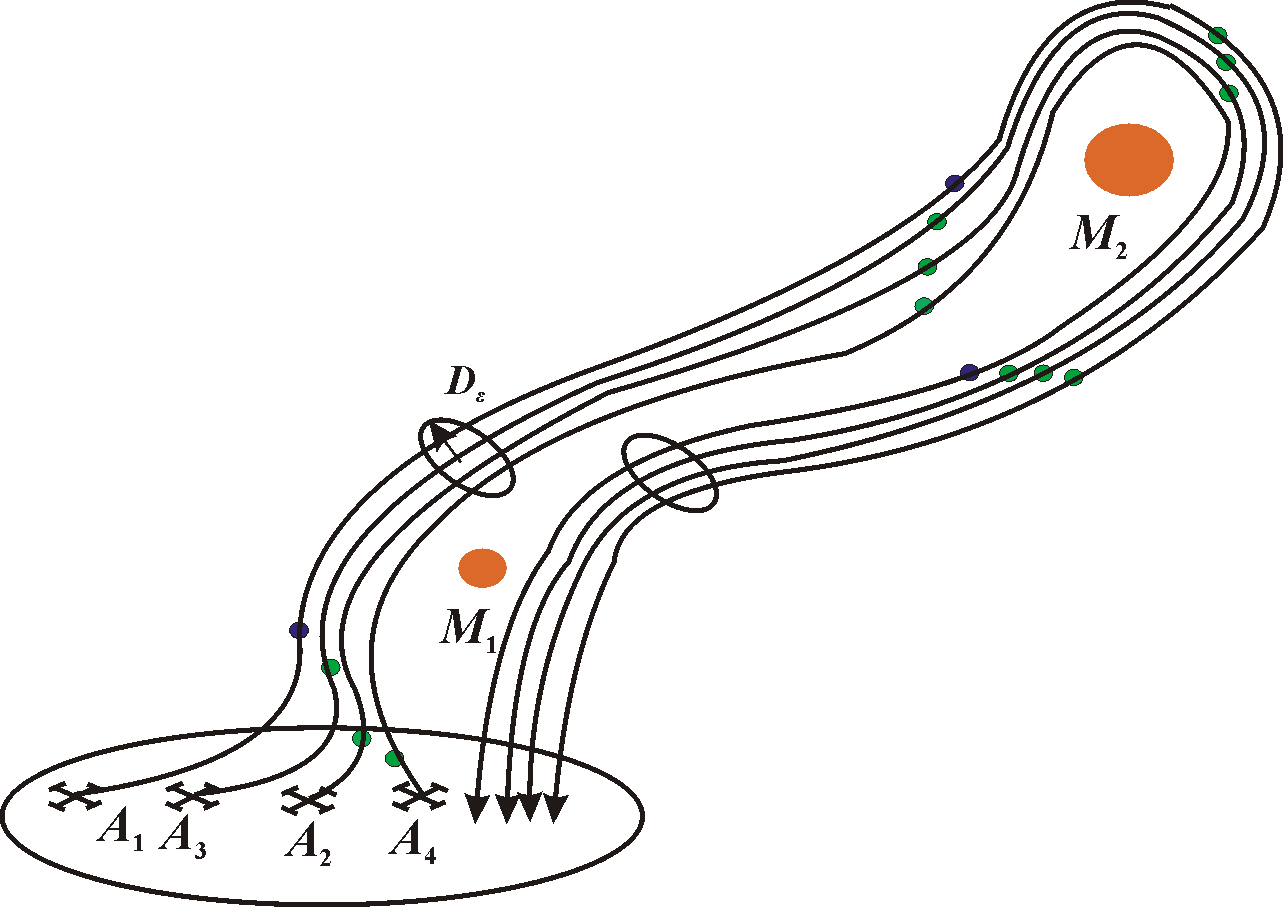
Let a swarm of N UAVs (further agents) that are indicated as A₁, …, A_n, which carry out some task in Euclidean space (x, y, z), for example monitoring or reconnaissance areas of the earth’s surface. For this purpose, agents can use known tactics such as “bearing”, “wedge” or other, or perform autonomous flight. On Figure 1 we can see the flight by “wedge” the group of UAVS, N=4.

Figure 1. Group of UAVs, N =4

Figure 1 shows the trajectory of UAVs group that forms multi-agent system from the 4-agents and performs the task of monitoring a predetermined route; where there are obstacles M₁, M₂ with known coordinates (x_M, y_M, z_M). To avoid collisions and saving group configuration when performing motion is assumed approximately equal velocity agents

Such formation of the agents’ behavior we can describe as aggregation with some centroid. In order to perform the task of group, each agent of aggregation is provided with means of communication and motion control. If members act in a limited size, additional members may be joined to this formation. Such formation is a swarm.

Let imagine structure swarm of UAVs as some formation of limited size. Using the terminology of [8], this is formation called aggregate with a center. We assume that each agent provided of communications and control means to carry themselves mission.

Each agent is moving in a three-dimensional Euclidean space. On its rout it can meet obstacles. The agent has vertical takeoff and landing (VTOL) and it therefore is can to bypass obstacles. Thus, agent i-th dynamic is described in space position as p_i with coordinates p_i = (x_i, y_i, z_i) and it has control signal u_i. We will describe the dynamic model of agent’s motion as an integrator of the second order in form [1, 5, 7]

Agents move in three-dimensional Euclidean space, in which can presented obstacles. Existing controls allow them to make the maneuver and get around obstacles. Let p_i is a position of i-th agent and u_i is a control signal in space, p_i = (x_i, y_i, z_i). Then the dynamic model of movement of i-th agent can be described by differential equations of the second order as [1, 5, 7]

In (1) р_i, u_i are functions of a time t. As in [8] we enter parameter D_e > 0, which characterizes the size of aggregate that for “t ® ¥ maintained control signals u_i

where position of central agent (leader) in aggregator

In (4) e is a constructive parameter, which is determined by the system developer. Equation (4) is a criterion to ensure the integrity of the group.

If on the route of UAVs is obstacles, group configuration is change, it selects a new type of configuration, which ensures their overcoming, in general, it slightly increases the parameter D(p_c) so as to ensure inequality D(p_c) £ D_e(p_c). This assume reconfiguring the formation in “a small” and does not change the overall objective of the group.

This paper concerns and solves the problem of the synthesis of the control of group from n UAV, which moves along the route, where there are natural obstacles fixed type, to ensure the fairness of condition D(p_c) £ D_e(p_c).

4.       Method of potential field

As in [6-8, 17], we submit multi-agent system a field of agents, which is formed by forces of attractive and repulsion. Attractive energy supports the chosen configuration, and the repulsion energy keeps agents from collisions among themselves and with obstacles.

As known [19], the energy of a potential attractive field is described by

where m > 0 is scaling factor, and Dp_i = || p_i – p_c || is the Euclidian distance between the i-th agent and the agent centric. The view of relation to centric agent A_c in uniform attractive field is show on Figure 2. This field is weaker in the center and stronger on edges.

Figure 2. Attractive field acting on agent A_c

Forces of attractive field is constructed as [20]

The repulsive energy is calculated as [19]

where n > 0 is scaling factor, d₀ > 0 is constant, which determines the maximum distance of action on the closest agent. Veiw of repulsive field built in accordance to (7) shown on Figure 3. This field is stronger in the center unlike attractive field.

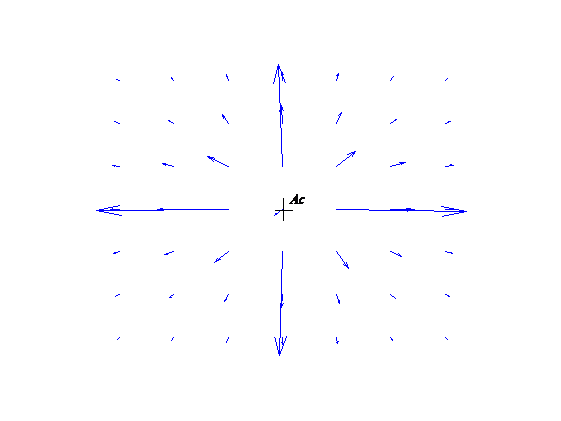Figure 3. Repulsive field acting on agent A_c

Repulsive forces similarly (6) we can represent as

In (8) p₀ is the coordinates to closest agent p_i or obstacle p_M, and is constant equal of maximum from all of their Euclidean distances.

Then, the general control law, which allows agents to achieve the objectives is the sum of components

where u_i is law of motion of i-th agent in the aggregation, and  components, which are determined by formulas (6), (8).

If the i-th agent is the leader of the group, then uⁱ = u^l.  Trajectory of leader determined the dynamics of its motion and described by equations, like (1)

where u^l is known law, the trajectories of other agents are being built respect to him. This approach allows to enter two terminate state such as start state (0, 0, 0) and final state (p_k, 0, 0) for each agent system.

Now consider the three types motion of the aggregation to follow on the route: along line, along curve, and with obstacles.

4.1.       Motion along line

In this case, the leader moves without acceleration. Then (10) is transformed into one equation

The mission of i-th agent is to save its position in a group, and to prevent exposure on other agents. The control law formed as a control

For agent leader is set j = l. Here k > 0 is the positive factor that define velocity of agent-member. In addition, there are a couple of small x_p1 ¹ 0, x_p2 ¹ 0 such that deviations |p_1i – p_1j| £ x_p1 and | p_2i – p_2j | £ x_p2, which occur in (12) and is needed to maintain stable movement.

If the leader is in the center of the group, its coordinates determined by equation (3), namely

where N* < N is the quantity of neighbors or agents in a group. Such type of motion is shown on Figure 4.

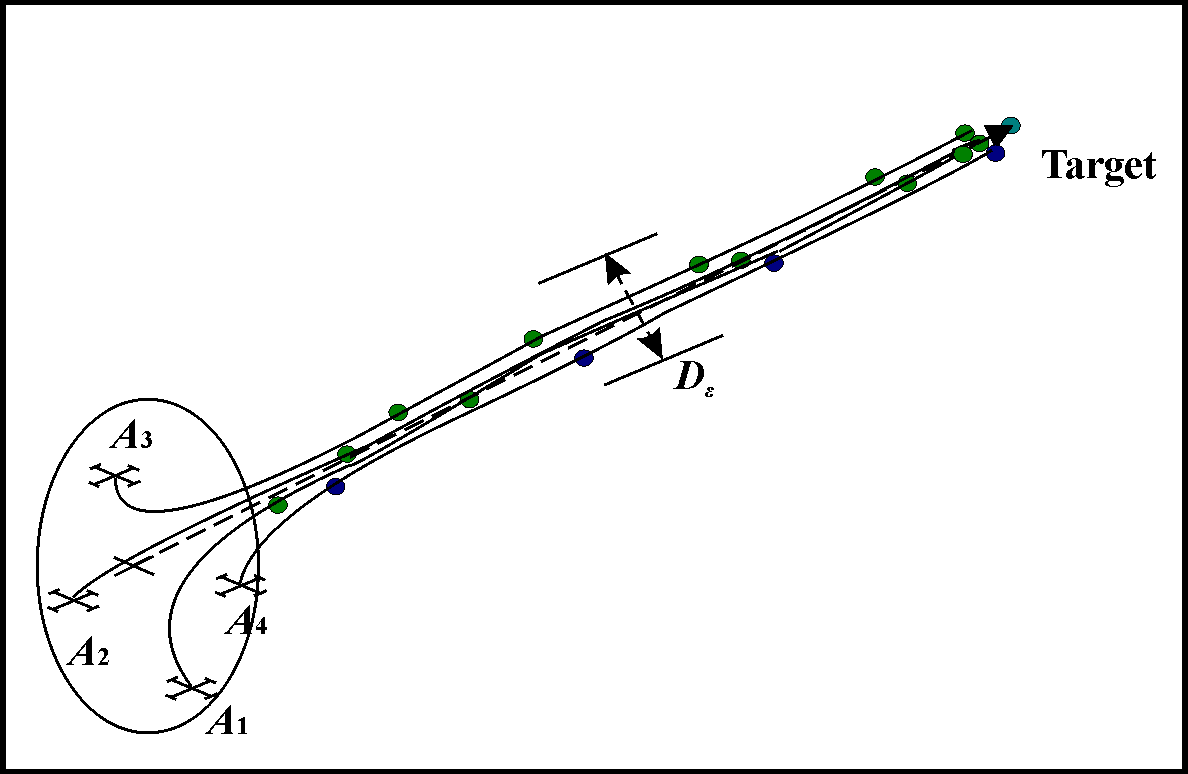Figure 4. Motion UAVs swarm along line

LEMMA 1. The movement of each agent of group that consist of N agents is described by system of differential equations of second order in form

where p = p_i – p_j is the appropriate coordinates of i-th and j-th agents, i ¹ j, i £ n, and j £ n. If j = l, is a leader of the group member.

Proof. This statement follows from (9), (11).

Corollary 1. Closed loop dynamic system (14) converges to the equilibrium position

Corollary 2. Agent-members velocity asymptotically converges to the agent-leader velocity.

Corollary 3. In system (14) coordinates p_i is p_i ¹ p_j for any i ¹ j, t ³ 0.

Corollary 4. If  is maximal size between UAVs in group, the size of formation is D (p) < D_e (p).

4.2.       Motion along curve

This type of movement is performed with an acceleration, condition (11) is not satisfied, and dynamic system (14) is transformed into

Coordinates p₁, p₂ in (16) coincide with the same coordinates in equation system (14), but control signal is value . This motion type is shown on Figure 5.

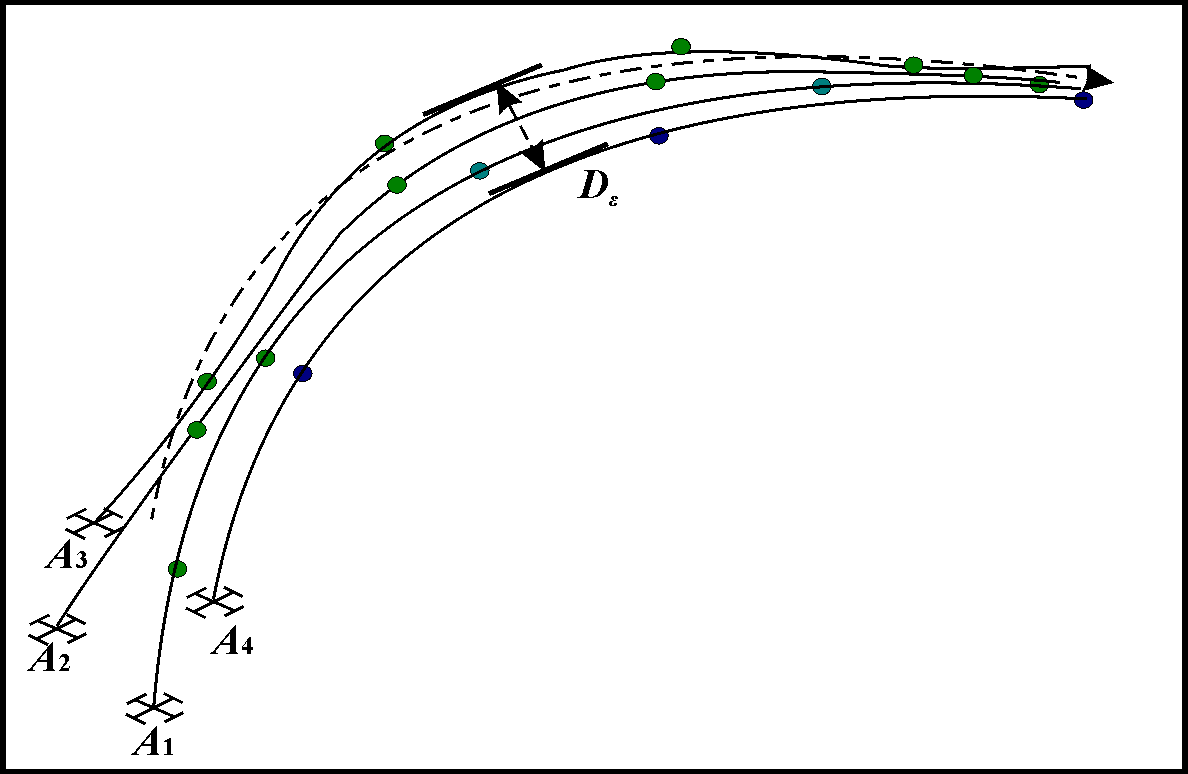Figure 5. Motion UAVs along curve

LEMMA 2. Let given factors k_y and k_p such as k_y > 0, k_p > 0 is true inequality , system (15) has exponential stability.

Proof. We represent the system of differential equations (16) in the form of a differential equation

where e_p = p_i – p_j, e_y = y_i – y_j, . If the k_p ¹ 0, and the (k_p, k_y, ) are positive factors, this equation can be represented as

Then condition of exponential stability of (15) is a negative real part of the roots (18) that is satisfied for .

Corollary 1. If k_y = 0, we have oscillation movement around leader with constant amplitude and it frequency is equal to .

Corollary 2. If > 0, we have asymptotically stability movement.

Corollary3. If , we have oscillation with error that is decreasing.

Corollary4. If , we have aperiodic movement of agent-member.

Corollary 5. If maximal size between UAVs in group is , size is D (p) £ D_e (p).

4.3.       Motion with obstacles

Existing approaches to the consideration of the motion agents with obstacles assume a repulsive force from the obstacle that is located on the route to goal. Action of this forces increases when agent is approaching to obstacle (deceleration of agent), and diminishes with distance. In order to bypass the obstacles, agent should make additional efforts that will lead to the deflection of the original route. It can be made by introducing repulsive force of the additive components of the agent respect to velocity and acceleration of motion

where n_aobs is a unit vector pointing from i-th agent to obstacle. The value p_1iobs shows agent movement, if p_1iobs> 0 is agent moving to obstacle and p_1iobs£ 0 moving from obstacle. Motion of N=4 agent in the presence of obstacles is shown on Figure 6.

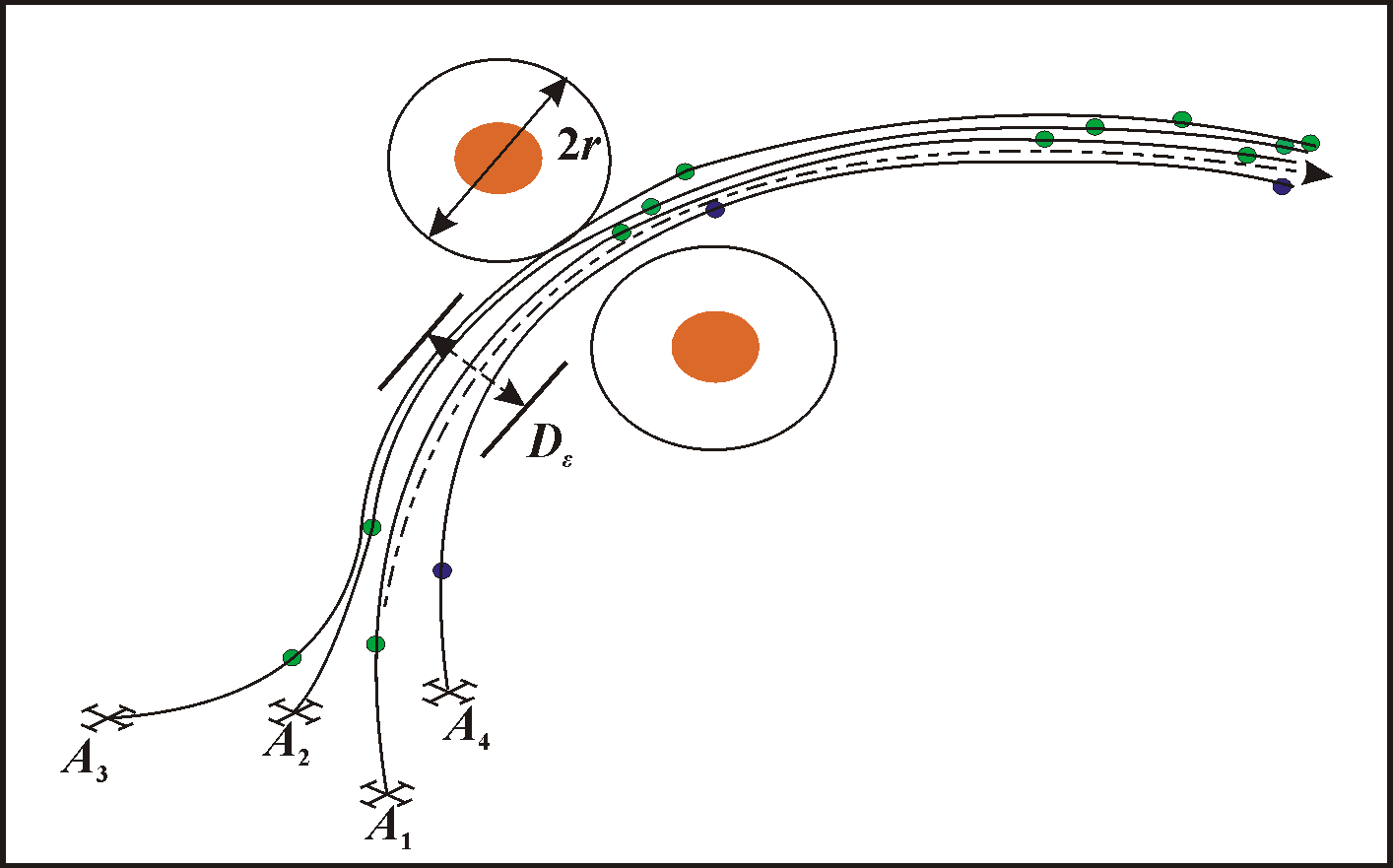Figure 6. Motion N=4 UAVs in obstacles

The order to overcome the obstacles type of bottlenecks, as shown in Figure 6, is determined by the control signal, that is defined by the equation (19), and UAVs are sorts in order decreasing its velocity, p_1N < p_1(N-1) < … < p₁₂ < p₁₁. Sorting can be done otherwise if you choose group leader as a reference.

5.       Quadrotor model

As a dynamic model of UAV selected model Quadrotor that management is simple, stable movement, the ability to hang in the air. A complete description of the model is described in [21]. Model of Quadrotor is presented by following equations system

Here (f, q, y) is the roll, pitch and yaw angles, I_{x, y, z} is the inertia UAV, J_r is the inertia rotor, l is the lever in coordinate system with the Quadrotor, k=1/m, m is the mass UAV, w is the rotor speed, and U₁, U₂, U₃, U₄, are calculated as

where b is the thrust factor, and d is the drag factor.

For simulation the model (25) is transformed to a space-state form , where Xι² is the state vector with the coordinates

In contrast to [21], which used to create a sliding mode for control, the control actions (U₁, U₂, U₃, U₄, u_x, u_y) of each agent are smooth functions of time t.

6.       Simulation

The motion of group of Quadrotors that moves in the potential field towards to goal on the route on which there are obstacles, is considered.

We assume that this group consists of three agent-members and one agent-leader. The route of agents gives start positions and goal position: p_A1=(100, 30, 0)^T, p_A2=(75, 20, 0)^T, p_A3=(130, 50, 0)^T, p_A4l=(110, 70, 0)^T, p_t=(600, 270, 0)^T. The coordinates of the located fixed obstacles on the route are known as p_o1 = (270, 130)^T, p_o2 = (220, 210)^T, and D_e (p_A) £ 50. The altitude of obstacles is higher than altitude of Quadrotors that lead to their maneuver in horizontal plane. The altitude for calculations is taken z = 10. The movement of agent-members and agent-leader to target is shown on the Figure 7.

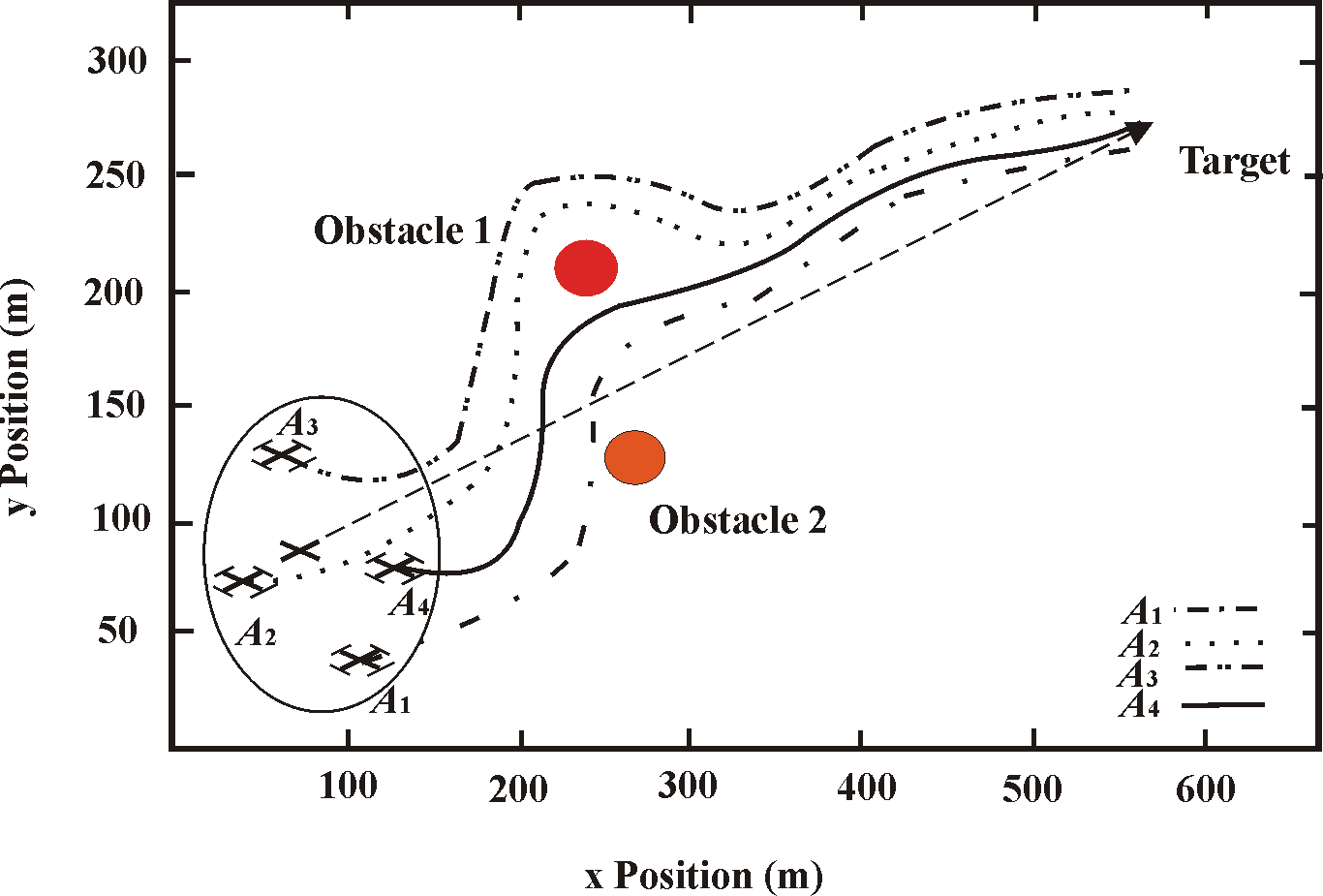Figure 7. Bypass movement of agent-leader and agent-members to the target

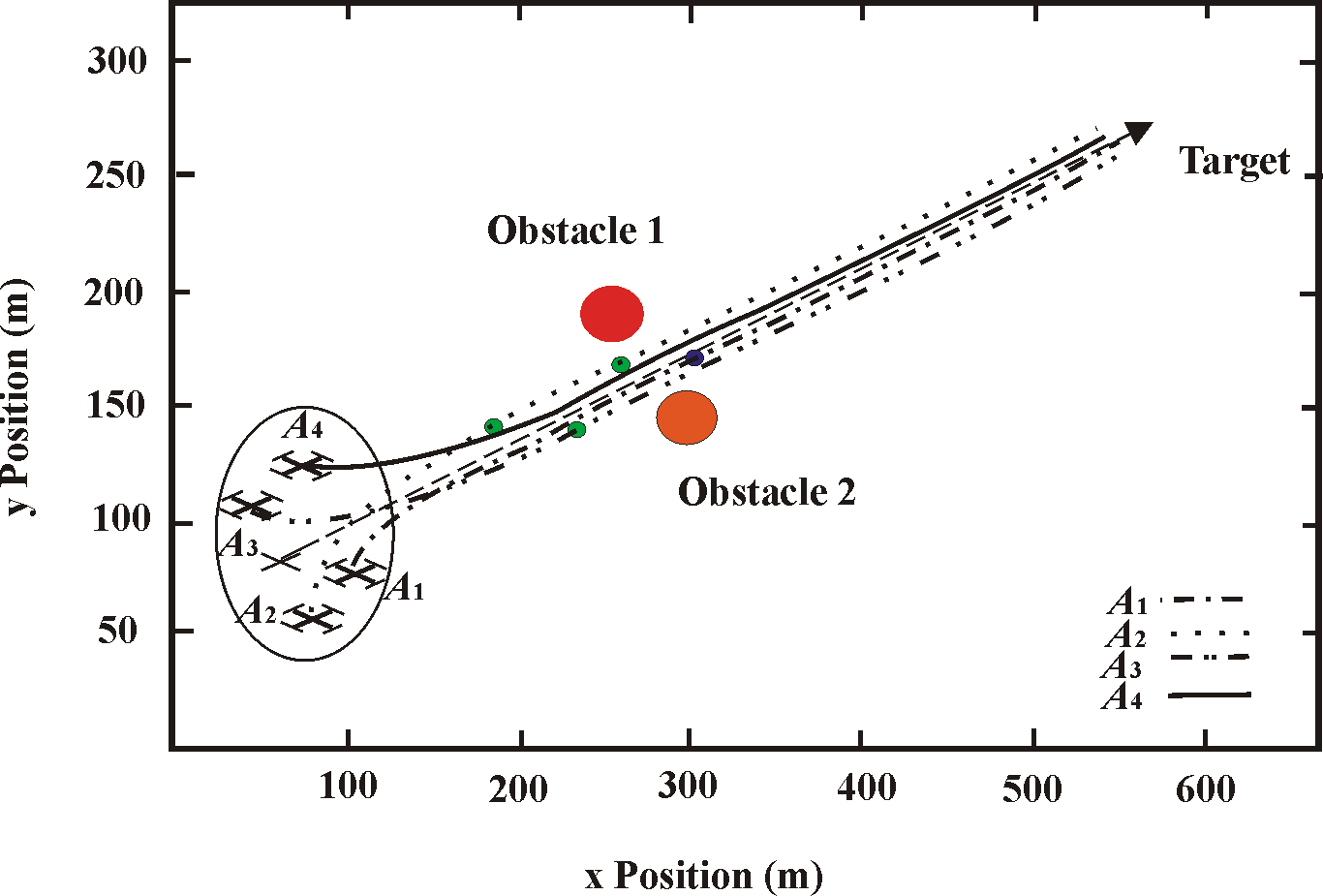Figure 8. Group of UAVs overcomes side-by-side obstacles by line type motion

Figure 7 shows that group of agents bypasses obstacles and continues its movement to target. Sometimes, when overcoming obstacles group of agents can change its formation size and the formation of agents is remains without changes, if there are no obstacles on the route,.

Figure 8 represents reconfiguration of the group of UAVs in line type motion, if there are located obstacles on the route side-by-side. In this case, the tactic of UAVs is similar to column and UAVs follow in rigidly defined order: A₄ ® A₃ ® A₂ ® A₁, where A₁ is the first and A₄ is the last.

7.       Conclusions

The paper presents a synthesis of control law of motion of multi-agent system to follow on the route on which possible the obstacles of movement. The feature of the proposed approach is synthesized control law with a smooth function of a time. Two ways of overcoming obstacles, one of them based at the bypassing and the other on reconfiguration are also shown. Control law is formed by two special potential functions, one of which creates an attraction force agents to the center of the structure, the other repels its from neighbors and obstacles. Configuration flight group in terms of obstacles to change, suggesting appropriate changes size and shape.

On the basis of the proposed control law created algorithm by which the simulation was conducted multi-agent system. Examples of the system behavior modeling show stable movement of the agents. Study of system parameters allow to ensure its stable movement and revealed relevant system parameters. Its behavior includes such stages as gathering into group, tracking on the given trajectory and avoidance of the obstacles. Research shows that successful simulation depends on such parameters as m and n of potential function.

In view of the fact that in the conditions of obstacles the movement along the curve is typical, because of which the signal in the control channels increase and it is switch it at a high speed, which is the so-called «sliding mode». The investigation of a multi-agent system in slide mode and effectiveness of proposed potential functions for movement one is the topic of our future research.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

Authors thank both the authorities of National Aviation University, National University of Defence of Ukraine and Central Research Institute of Armaments and Military Equipment of the Armed Forces of Ukraine for their support during the preparation of this paper.

1. D.P. Kucherov, A.N. Kozub, O.N. Kostyna “Group Behavior of UAVs in Obstacles Presence”, proc. IEEE 4th Int. Conf. “Methods and Systems of Navigation and Motion Control (MSNMC)”, Kyiv, Ukraine, 2016.
2. M. Wooldridge, An Introduction to multi-agent systems, John Wiley & Sons Ltd, 2009.
3. Benu, C. Goel, Sheenam, “Ant Colony Optimization for Wireless Sensor Network: A Review”, IOSR-JCE, 17(3), 89-92, 2015.
4. W.Y.J. Chou, L. Marsh and D. Gossink “Multi-Agent Coordination and Optimisation in the RoboCup Rescue Project”, proc. 18th World IMACS / MODSIM Congress, Cairns, Australia, 2009.
5. A. A. Bandala, E. P. Dadios, R. R. P. Vicerra, L. A. G. Lim “Swarming Algorithm for Unmanned Aerial Vehicle (UAV) Quadrotors – Swarm Behavior for Aggregation, Foraging, Formation, and Tracking”, J. of Advanced Comput. Intell. and Intell. Inform., 18(5), 745 – 751, 2014.
6. L. Yin, Y. Yin, and C.-J. Lin, “A new potential field method for mobile robot path planning in the dynamic environments”, Asian J. of Control, 11(2), 214-225, 2009.
7. A. D. Dang, J. Horn, “Intelligent Swarm-Finding in Formation Control of Multi-Robots to Track a Moving Target”, Int. J. of Computer, Electr., Autom., Control and Inf. Eng., 8(4), 561 – 567, 2014.
8. V. Gazi, B. Fidan, Y. S. Hanay, M.I. Köksal, “Aggregation, Foraging, and Formation Control of Swarms with Non-Holonomic Agents Using Potential Functions and Sliding Mode Techniques”, Turk. J. of Electr. Eng., 15 (2), 149-168, 2007.
9. L. Zhang, H. Gui, “Optimal Strategies for Agents in an Alternating Offers Negotiation Protocol Considering Time Constraint”, J. of Autom. and Control Eng., 4 (4), 313 – 318, 2016.
10. D.K. Jesintha, J.P. Anandh, M. Ramnath “Dynamic analysis of agent network in self organization using service level agreement technique”, Int. J. of Eng. Sci. Invent., 4 (3), 44 – 49, 2015.
11. L. Marsh, G. Calbert, J. Tu, D. Gossink, H. Kwok, “Multi-Agent UAV Path Planning”, Int. Congress on Modelling and Simulation, MODSIM05. Modelling and Simulation Society of Australia and New Zealand, 2005.
12. M. Shanmugavel, A. Tsourdos, B. A. White, R. Zbikowski “Differential Geometric Path Planning of Multiple UAVs”, Trans. of ASME J. of Dyn. Syst., Meas., and Control, 129(3), 620-632, 2007.
13. D.P. Kucherov, “Agent-based approach to the problem movements by the route”, Visnik of the Volodymyr Dahl East Urk. National University, 4 (211), 168 – 171, 2014.
14. İ. Çuhadar, M. Dursun “Unmanned Air Vehicle System’s Data Links”, J. of Autom. and Control Eng., 4 (3), 189-193, 2016.
15. D.P. Kucherov, A.N. Kozub “Control System Objects with Multiple Stream of Information”, proc. IEEE 3rd Int. Conf. Actual Problems of UAV Developments (APUAVD)”, Kyiv, Ukraine, 2015.
16. Y. Wang, C. Hu, “Moving as a whole: multirobot traveling problem constrained by connectivity”, Turk. J. of Electr. Eng. & Comput. Sci., 23, 769 – 788, 2015.
17. A. D. Dang, J. Horn,“Formation Control of Leader-Following UAVs to Track a Moving Target in a Dynamic Environment”, J. of Autom. and Control Eng., 3 (1), 1-8, 2015.
18. MD. A. A. Ansary, M. M. Hasan, “An Intelligent Line Following Robot with Obstacle Detection”, Int. J. of Sci. and Eng. Investig., 5 (53), 44-48, 2016.
19. M. C. Jain, Textbook of Engineering Physics, (Part I): PHI Learning Private Ltd, 2009.
20. G.A. Korn, T. M. Korn, Mathematical handbook for sceintist and engineers: McGraw-Hill Company, 1968.
21. S. Bouabdallah, R. Siegwart, “Backstepping and Sliding-mode Techniques Applied to an Indoor Micro Quadrotor”, proc. IEEE Int. Conf. on Robot. and Autom., Barcelona, Spain, 2005.

(Click to view)

(Click to view)

No. of Downloads Per Month

No. of Downloads Per Country