1. Introduction

The correlation-based stochastic models (CBSMs) are mainly used for theoretical analysis to assess the performance of massive MIMO systems. However, these models could be applied to cases where the user equipment (UE) with multiple antennas works at millimeter wave [1]. Although the fifth generation (5G) wireless communication technology will offer alluring features such as higher transmission rate, there are still several challenges ahead in the deployment of this technology [2-3]. Very recently, antenna arrays have attracted attention in the wireless communication industry to enhance signal quality, coverage and capacity. This is because antenna configuration directly influences the channel characteristics and performance, therefore, it is a critical factor in deciding the channel characteristics in MIMO technology.

In view of this, all attempts to improve the performance of the existing MIMO technology must be investigated especially in regards to realistic channel models.

All endeavours to improve and enhance the performance of the existing MIMO technology need to be explored, specifically with regards to analyzing the MIMO characteristics of wireless channels. The authors in [4] demonstrated that having the MIMO system in three dimensional view is the efficient method for managing spatial resource. Several array configurations have been the subject of investigations on MIMO technology, and most of the prior investigations considered simple system configurations using only AS [5–9].

Many refer to the work in [8] and [9] where researchers presented spatial correlation function for four-element receiving circular arrays, when the angle-of-arrival (AoA) followed Laplacian and truncated Gaussian distributions respectively, because the uniform circular array (UCA) configuration has been the subject of many investigations on MIMO technology. Although the authors derived the correlation function for UCA in terms of AS by considering that the ES of the incoming plane wave in the propagation geometry is 90^o, their contribution provides fundamental basis for evaluating the spatial correlation function of URA in advanced MIMO technologies. Therefore, our objective in this paper is to experiment the CBSMs at 2.4 GHz. We modelled the transmitter as a uniform rectangular array, and examined the effects of spatial fading correlation and mutual coupling on channel capacity and symbol error rate (SER). To prove our concept, we quantify the mutual coupling of the receiving array by the receiving mutual impedance method (RMIM) [10], whereas, we examined the URA in the CST Microwave Studio to determine the coupling matrix. Recently, authors in [11] proposed a spatial correlation function for MIMO channel model on the latest 3GPP standards and WINNER+ [12]. We are of the view that our concept will add to cover new aspects in MIMO modelling studies.

For purposes of clarity, the contributions in this paper are as follows: 1) We fabricate a decoupling network to study the dependence of system performance on antenna spacing, AS and ES of MIMO system, using CBSMs on the assumption that the magnitude and phase of the mutual coupling and consequently the coupling matrix of the coupled array varies from that of the decoupled array at the receiving end. 2) We derive an analytical expression for spatial correlation function of a URA, based on maximum power in the direction of maximum arrival using the Student’s t-distribution. 3) Our outcomes show that azimuthal spread (AS) is the essential determinant of system performance. Also, lower values of AS and ES increase the rate of deterioration in the SER, and not antenna spacing.

This letter is organized as follows: Section II presents the design of the decoupling network. In Section III, we derive the closed-form expression for the spatial correlation function in terms of maximum power for URA using Student’s t-distribution. Section IV presents analytical and simulation results. Finally, we give concluding remarks in Section V.

2. Operating Matrix of the Decoupling Network

The compensation network is designed using a power-divider and two rat-race couplers. The power divider has unequal power-dividing ratio with no active circuit elements to minimize extra circuit noise. The operating matrix for two-element receiving array is given by [13].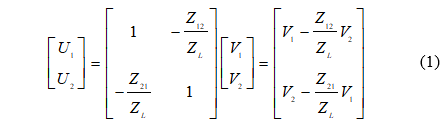

where the inputs to network are coupled voltages V₁ and V₂ from the two monopole antennas, and the outputs of network are compensation voltages U₁ and U₂. The mutual impedance between the two monopole antennas is represented by Z₁₂ and Z_L is the matched load impedance. In order to achieve the tri-band operation, we utilized resonators and stubs.

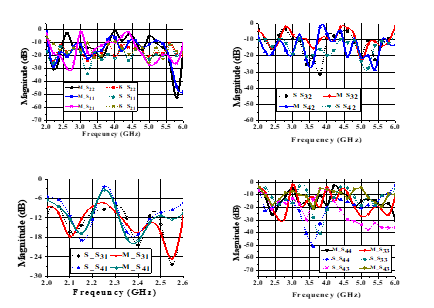
By sharing the stub with the resonator (parallel LC circuit) of two adjacent -shaped structure circuits within the rat-race couplers, a decoupling network with working frequencies 2.4/3.5/5.5 GHz was designed. The length and impedance of stubs at different frequencies are calculated using the procedure in [14].  The decoupling network has been designed using ADS and fabricated using FR4 substrate with dielectric constant 4.8 as shown in Fig. 1. Simulated and measured responses are shown in Fig. 2. Measured results at 2.4/3.5/5.5 GHz demonstrate that isolation and insertion losses between input and output ports of more than 10 dB can be accomplished. To achieve best performance, the initial values of the impedance and the parallel resonator had to be increased to accomplish the tri-band operation. This accounted for the large differences between simulated and measured values in Fig. 2(a) and Fig. 2(b) at 3.5 GHz.

3. System Model

3.1.  Proposed Spatial Correlation of URA

The spatial correlation between antennas at positions  and following the procedure in [14] is expressed as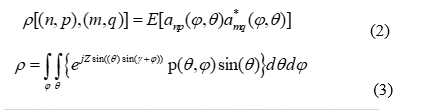

where is the joint spatial power spectrum. For our theoretical analysis, we have used the fact that the maximum power in the direction of maximum arrival is proportional to . Therefore, we represent the joint spatial power spectrum in (3) by the maximum power  of the incident plane wave and proportional to AS and ES. If the phase gradient has a Student’s t-distribution as in [15], compared to the choice of joint spatial power spectrum of [14], then the phase in (3) can be expressed as , where . Following the methodology in [15], the probability density function of according to Student’s t-distribution is given by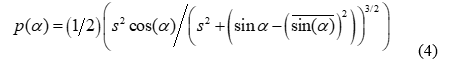

where  are the antenna, load and mutual impedances respectively. With the above assumption that the magnitude and phase of the mutual coupling are different, we used RMIM measurement procedure shown in Fig. 3 to evaluate the mutual coupling between small receiving monopole arrays at the receiving end under two conditions [10] describe in Section IV.  The mutual impedance is expressed as [10]

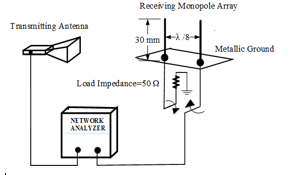
4. Numerical Results

In this section, we present the analytical performance and the simulation results of MIMO system using CBSMs. We modelled and analyzed the correlated-based stochastic MIMO channel, based on the two conditions that the magnitude and the phase of the mutual coupling and the coupling matrix of the coupled receiving array vary much from that of the decoupled array. The simulated channel is according to (6)-(10) and it is assumed that fading is correlated at both transmitter and receiver sides. The receiving array is represented by two-monopole element on a metallic ground and operating at 2.4 GHz. The monopoles have length of 30 mm, radius of 0.5 mm and element separation of . As indicated already, the formulation of coupling matrix of the receiving array is determined in anechoic chamber under two conditions using RMIM.

Condition I: the S-parameters of the coupled array are determined to estimate for the coupled voltages ( and ), and also to formulate the coupling matrix using (9)-(10).

Condition II: the monopole array is connected to the decoupling network through equivalent length coaxial links. The scattering parameters of the output ports of the decoupling network are determined to formulate the coupling matrix and estimate for the compensated voltages ( and ).

With the end goal of justifying the assumption that the magnitude and phase of mutual coupling of coupled array differs much from the decoupled array at the receiving end, there are three different types of voltages recorded in Table I. The last row in Table I is a ratio of the voltage obtained with monopole B to the voltage obtained with monopole A. It can be seen that the ratio of the compensated voltage is very close to the uncoupled voltages. This also demonstrates that the compensated voltages have successfully been removed off the coupling effect. The value of  is determined for each antenna spacing of the URA and incorporated into the channel model.

4.1.  Effects of AS and ES- Performance Tradeoff

We explore the dependency of narrowband MIMO channel capacity using uniform power allocation on AS and ES at different antenna spacing using CBSMs. Our results according to the modelling of coupling capacity matrix at the receiving side in Fig. 4 and Fig. 5 support the existing fact of the effects of higher values

of azimuthal spread (AS) on system performance. Our outcomes demonstrate that elevation spread (ES) does not affect system capacity as much as the azimuthal spread (AS) does. Moreover, it is therefore not surprising that spacing between antenna elements affects system performance. However, larger number of transmit antennas improve system performance in a fixed physical space.

4.2.  Symbol error rate (SER) vs SNR

In Fig. 6, there is a close match between symbol error rate (SER) for at  and respectively. We observed that the SER after an increase of 10dB for ,  at  remains nearly the same as that for , at . A close inspection of Fig. 6 reveals that the impacts of higher values of AS and antenna spacing on the channel capacity are more significant than SER. We note that lower values of AS and ES increase rate of deterioration in the SER and not antenna spacing after decoupling process.

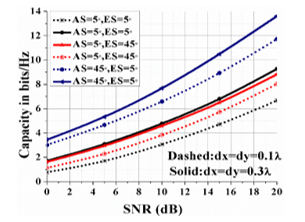
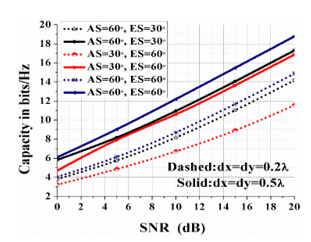
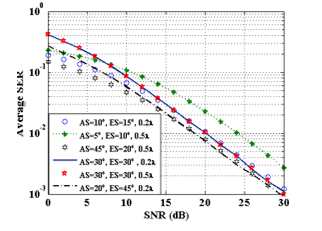
Table 1: Different Measured Voltages

		Uncoupled Voltages (reference)	Coupled voltages	Compensated voltages
Monopole A	mag (mV)	16.64	12.4	11.55
	angle ( )	-160.64	-166.67	34.967
Monopole B	mag (mV)	16.54	15.42	12.30
	angle  ( )	-139.56	-141.46	55.16
B/A	mag (mV)	0.9939	1.2199	1.065
	angle ( )	21.08	25.208	20.193

5. Conclusion

We derived an expression for the spatial fading correlation of URA when the phase gradient follows Student’s t-distribution. We investigated dependency of MIMO performance on azimuthal spread (AS) and elevation spread (ES) after decoupling process using CBSMs. Our results support the existing fact that the azimuthal spread (AS) is the essential determinant of system performance. Additionally, results confirm that lower estimations of AS and ES significantly expand the rate of deterioration in the SER, and not antenna element separation after decoupling process.

Appendix

The integral in (5) is evaluated in this appendix. Using the properties of Bessel function in the case of  as [17]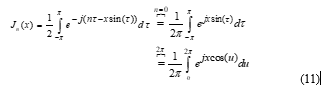

1. Kan Zheng, Suling Ou and Xuefeng Yin “Massive MIMO Channel Models: A Survey “International Journal of Antennas and Propagation”, 2014, Article ID: 848071, Jun. 2014.
2. Asvin Gohil, Hardik Modi and Shobhit K Patel “5G Technology of Mobile Communication: A Survey, IEEE Conference on Intelligent Systems and Signal Processing (ISSP), pp. 288 – 292, March
3. Kan Zheng, Suling Ou and Xuefeng Yin “Massive MIMO Channel Models: A Survey”, International Journal of Antennas and Propagation, vol. 2014, Article ID 848071, June 2014.
4. Jianhua Zhang, Chun Pan, Feng Pei, Guangyi Liu, and Xiang Cheng “Three-Dimensional Fading Channel Models: A Survey of Elevation Angle Research,” IEEE Communications Magazine, June 2014, pp. 218-226
5. Zhou, S. Sasaki, S. Muramatsu, H. Kikuchi, and Y. Onozato, “Spatial correlation for a circular antenna array and its applications in wireless communication,” in IEEE Global Telecommunications Conference, GLOBECOM ’03., vol. 2, Dec 2003, pp. 1108–1113.
6. A. Forenza, D. J. Love, and R. W. Heath, “Simplified spatial correlation models for clustered MIMO channels with different array configurations,” IEEE Transactions on Vehicular Technology, vol. 56, no. 4, July. 2007, pp.1924–1934.
7. -A. Tsai and B. Woerner, “The fading correlation function of a circular antenna array in mobile radio environment,” in IEEE Global Telecommunications Conference, vol. 5, May 2001, pp. 3232–3236.
8. Jiann-An Tsai, R. Michael Buehrer, and Brian D. Woerner “BER Performance of a Uniform Circular Array versus a Uniform Linear Array in a Mobile Radio Environment”, IEEE Transactions on Wireless Communications, vol. 3, No. 3, May 2004, Page: 732.
9. Jiann-An Tsai, R. Michael Buehrer “Spatial Fading Correlation Function of Circular Antenna Arrays With Laplacian Energy Distribution”, IEEE Communications Letters, vol. 8, No. 5, May 2002, Page: 295
10. T. Hui, “A new definition of mutual impedance for application in dipole receiving antenna arrays,” IEEE Antennas Wireless Propag. Lett. vol. 3, pp. 364–367, 2004.
11. Qurrat-Ul-Ain Nadeem, Abla Kammoun, M’erouane Debbah†, and Mohamed-Slim Alouini “Spatial Correlation Characterization of a Uniform Circular Array in 3D MIMO Systems,” International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), July 2016, pp: 1 – 6
12. 3GPP TR 36.873 V12 .0.0, “Study on 3D channel model for LTE,” Sep.2014
13. Yu and H.T. Hui “Design of a Mutual Coupling Compensation Network for a Small Receiving Monopole Array”, IEEE Trans. On Micro. Theory and Techniques, vol. 59, no. 9, pp. 2241-2245, Sept. 2011.
14. K. Yong and J. S. Thompson, “A three-dimensional spatial fading correlation model for uniform rectangular arrays”, IEEE Antennas and Wireless Propag. Lett, vol. 2, no. 1, pp. 182–185, 2003.
15. B. Andersen and K. I. Pedersen, “Angle-of-arrival statistics for low resolution antenna”, IEEE Trans. Antennas Propagat. vol. 50, No. 3, pp.391-395, Mar. 2002.
16. Masouros, J. Chen, K. Tong, M. Sellathurai, and T. Ratnarajah, “Towards massive-MIMO transmitters: on the effects of deploying increasing antennas in fixed physical space,” in Proc. of the Future Network and Mobile Summit, pp. 1–10, 2013.
17. Abramowitz Milton, Stegun Irene “Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables”, New York: Dover, ISBN 0-486-61272-4.
18. Herbert Bristol Dwight, “Tables of Integrals and other Mathematical Data”, 3rd ed, Macmillan Company, New York, 1957.

(Click to view)

(Click to view)