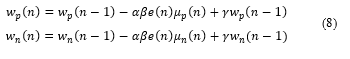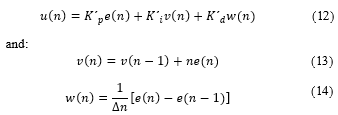1. Introduction

Two-wheeled robots have some advantages over other types of mobile robots. The wheel configuration makes them highly maneuverable and still easier to control than legged robots. Having no more than two wheels means more room for larger wheels, potentially allowing them to traverse rougher terrain. In the last decade, auto-balance two-wheeled robots have been intensively discussed [1], [2], [3].

The dynamics of two-wheeled robots have some particular features which complicate their control. Specifically, they are non-minimum phase, under-actuated and also unstable in open loop. Therefore, robust mechanisms of auto-balance are very important to these dynamics systems, requiring proper control based techniques based on suitable sensing.

Many controller designs have been investigated for the auto-balance two-wheeled robot [4]. Proportional-Integral-Derivative (PID) controllers are widely used in many areas in industry, because no model of the plant is required, with tuning of just three gains [5]. However the purpose of an intelligent control method is to minimize the stress of control applied for complex plants.

The hybrid systems based on fuzzy logic have demonstrated their capacity of resolve several types of problems in many applications, as in robotic. Using one algorithm based on the gradient descent method, with a cost function using only the error

signal, is possible to obtain one controller with good performance, [6], [7]. An important example is the ONFC controller (Online Neuro Fuzzy Controller) [8], which represents one structure with three synaptic weights.

Also, artificial neural networks (ANN) are commonly used as a strategy of adaptive control for auto-balance two-wheeled robots. The algorithm executes the learning process of neural network, where the synaptic weights are adjusted, during the execution of the network as the goal to reach the desired result [9]. The equilibrium will be improved during the neural network learning process.

Moreover, for outdoor applications the robot should also be able to stabilize on inclined or uneven terrain. This invites researchers to design controllers for the control of the stability of two-wheeled robots on inclined terrain at the desired speeds and implemented in real time.

The proposal of this work is to implement intelligent algorithms to control an auto-balance two-wheeled robotic system that can be able to move in terrains with some irregularity.

2.       System Formulation

2.1.  Two-Wheeled Robot Dynamic Model

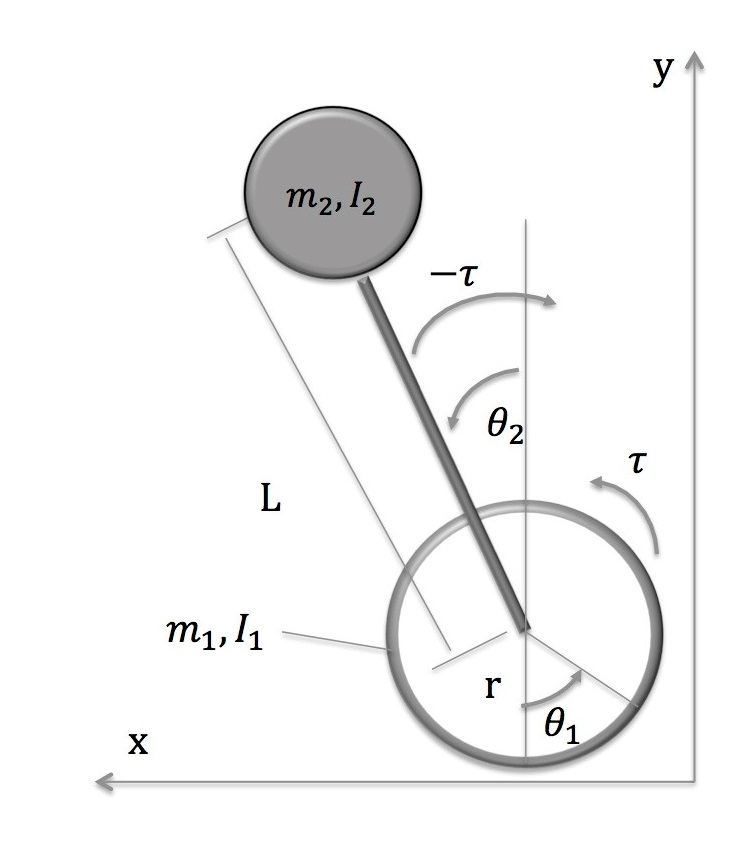
Figure 1 shows the structure of an two-wheeled robot where m₁ [kg] is the mass of each wheel; m₂ [kg] is the mass of the body; I₁ [kgm²] is the inertial moment of the wheel in relation to the gravity center; I₂ [kgm²] is the inertial moment of the body in relation to the gravity center; r [m] is the wheel radius; L [m] is the distance of the mass center of body to axis rotation of wheel; τ₁ [Nm] is the wheel torque and τ₂ [Nm] is the body torque; θ₁ is the rotation angle of each wheel in degrees; θ₂ is the inclination angle of the body in degrees.

Based on Newton’s equations of motion, the dynamic modeling of the robot is described by

3.       Controller Design

The primary objective in the control of two-wheeled robots is always to remain balanced and avoid toppling. Secondary objectives may include tracking a certain speed or trajectory.

In the prototype, there were implemented the balance and position control. For the balance control all variables are subtracted of the desired reference value. Therefore, null vector is the condition of auto-balance:

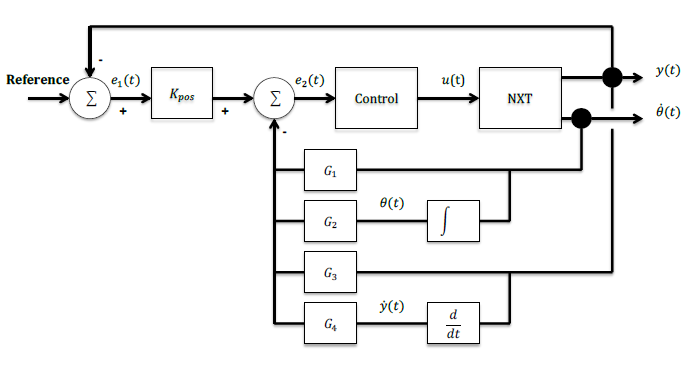
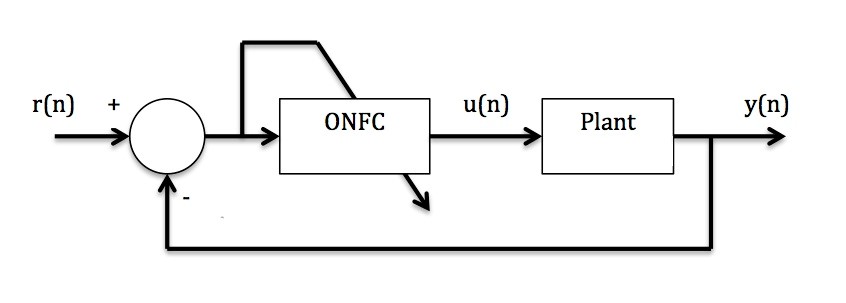
For the position control, the variable of the encoder, y, is feedback and subtracted of the reference value. The position control uses the proportional controller gain, K_pos. The complete strategy of control is showed on the diagram of Figure 2

3.1.  Online Neuro Fuzzy Control

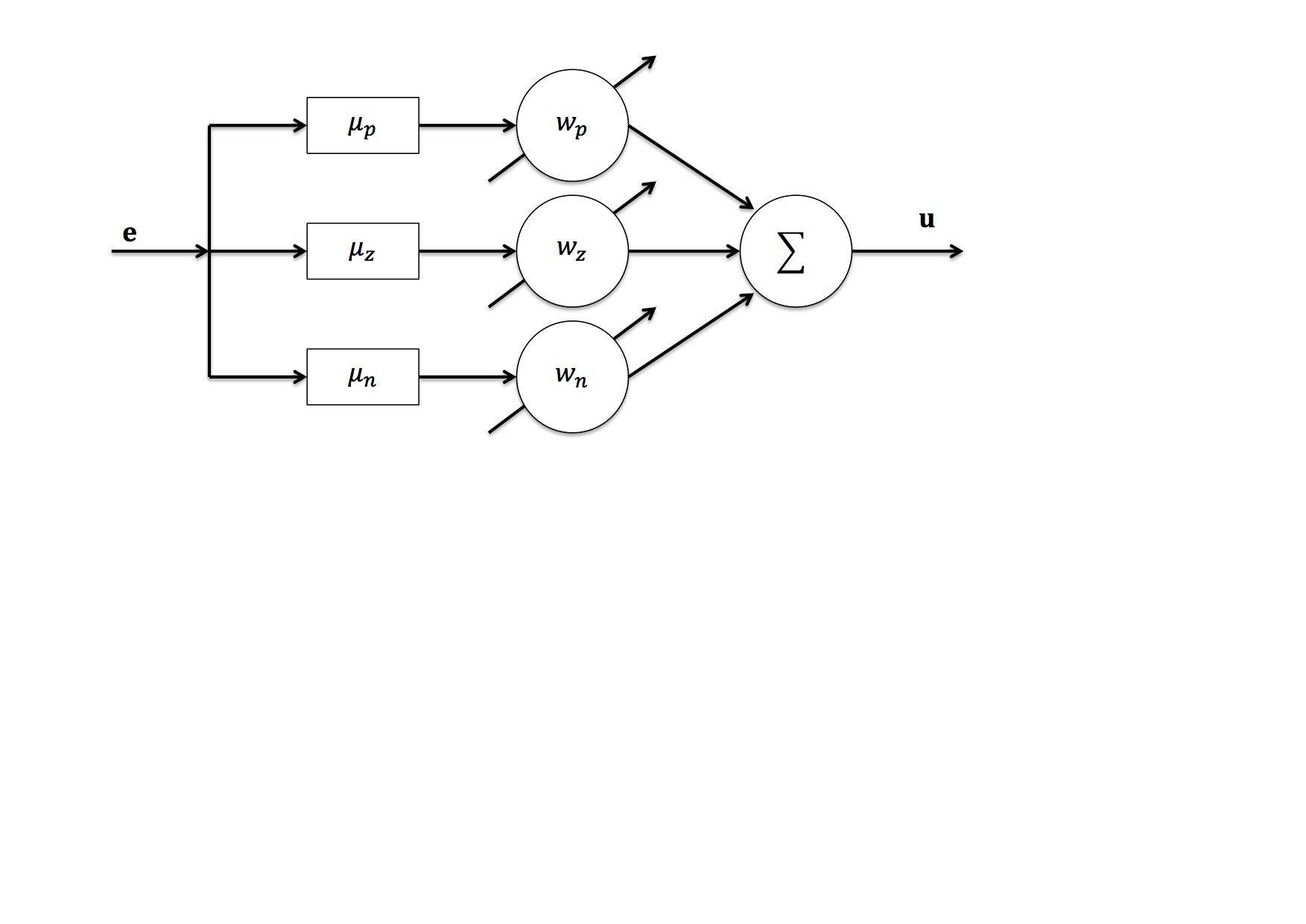
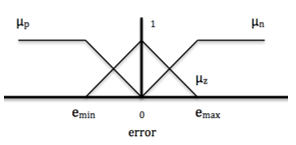
Reference [3] presents the Online Neuro Fuzzy Control (ONFC) to the implementation of the online algorithm. Figure 3 shows one block diagram of the generic system using the ONFC control and its internal structure. The ONFC control uses only three membership functions (triangular and complementary) as it can be seen in Figure 4. For all values in the universe of discourse, the sum of the three membership functions µ_p, µ_z and µ_n should be equal to (5).

The control output, u, is defined based on Sugeno model of zero order. Since the membership functions are complements, the output can be written as:

If the error is limited and zero average, the weight w_z will be limited through of cost function. The same is not valid to the weights w_n and w_p, that could be unlimited for any disturbance signal in the error or for intermittent variations of the reference.

The update of weights is realized by gradient descent defined by the following cost function, J, described by (7)

where n is the discrete time, e is the error between the desired and obtained signal of the system and γ is one factor between 0 and 1 and will determine the decay rate of the weights adjusted according to the plant used.

Through this cost function, it´s possible to obtain the equations (8) to perform the update of the weights in order to minimize

where β is one parameter dependent of the plant and unknown.

3.2.  Artificial Neural-Networks Control

The Proportional-Integral-Derivative Neural-Networks (PID-NN) controller [4] is based on the discrete equation model of the transfer function of the PID control.

First, the PID-NN is trained off-line and the data are generated by one simulated PID system and used for training the neural network. The learning is supervised and the desired goal is to minimize the sum of the squared errors, E_sq, of the trained data.

Combining the equations of the discrete time PID controller, we can obtain one recurrent neural network (Figure 6). The input of network is the error signal e(n) and the output of the control signal is u(n). Activation functions of the neurons are linear. The Figure 6 also shows the gains K_p, K_i and K_d of the neural network control structure. They are the weights, which can be adjusted. The rest of the weights present constant values. Considering O₁(n), O₂(n) and O₃(n) the outputs of neurons of hidden layer, the output of the network could be computed by the equations: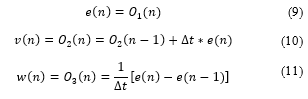

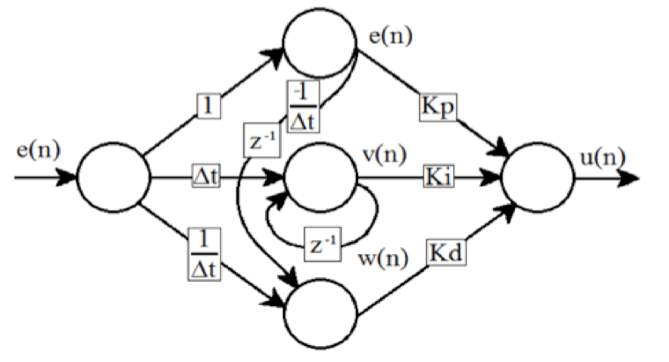
The equation of control in discrete time can be seen in (12)

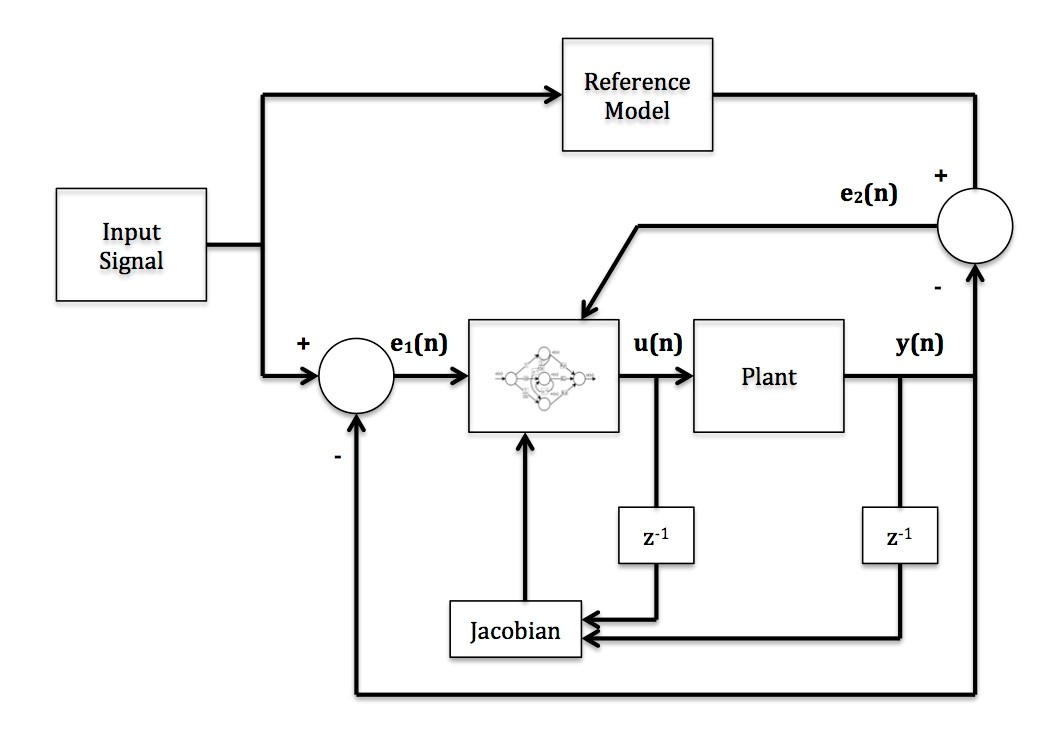
After the off-line training, the PID-NN is combined in series with the system for online tuning, as observed in Figure 7. In this form of learning, the update of the weights is done before the presentation of each example of training. The difference between the response of the output of the plant and the reference signal generates the error e₁ that will be the input signal of the controller. The error e₂ is generated by difference between the response of the output of the plant and the response of the reference of the model. This signal is directly related with the update of the online weights.

According to the method of gradient descent, the weights update follows the equations: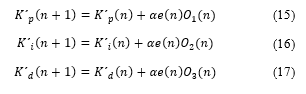

4.       Experimental Study

4.1.  Hardware Implementation

Figure 8 shows the robot system used in the experiments. The hardware of whole system includes a microcontroller (AT91SAM7S256), gyro sensor (NGY1044), ultrasonic sensor, servomotors and structural support parts. Although the system has ultrasonic sensor it was not used in these experiments at this moment.

4.2.  PID Control

Table 1 shows the gains of the Proportional-Integral-Derivative (PID) control of the two-wheeled robot based on the Ziegler-Nichols method. These results will be necessary to compare the performance of the other controllers.

The experimental tests have shown   that K_d gain needs to be reduced to 0.000504 to ensure system stability. The proportional gain K_pos to position control was obtained by trial and error. The best value found was K_{pos =} 0.495.

4.3.  Computational Model

The simulation platform of the two-wheeled robot was developed in the MatLab-Simulink software. The computational model was validated to reproduce the same response of the auto-balance two-wheeled robot during its operation in the real world. The correlations between the simulated and experimental results were satisfactory considering the nonlinearity of the system.

Table 1: Initial PID gain based on Ziegler-Nichols method

4.4.  ONFC Control Implementation

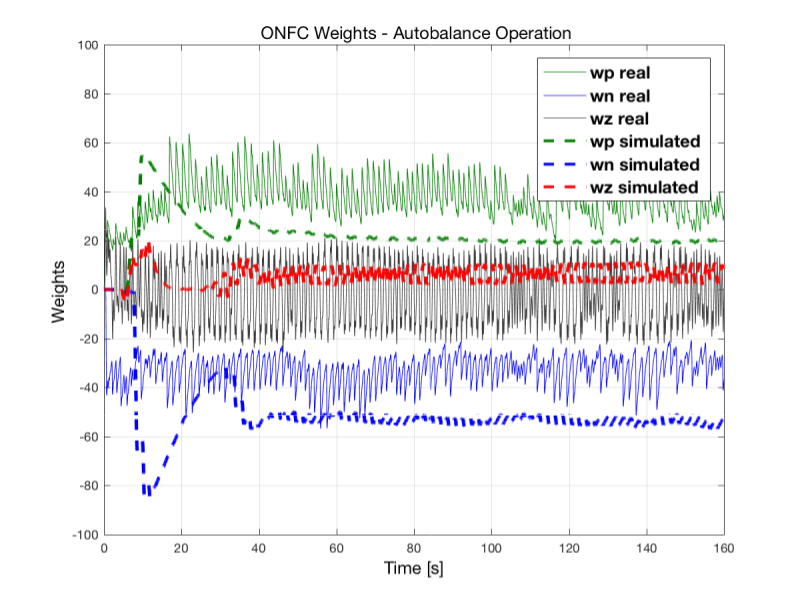
To evaluate the effectiveness of the proposed architecture, the proposed ONFC controller is implemented and equipped in the two-wheeled robot. The proposed control laws are represented in equations (5-8). To tune the ONFC control, several real experiments in the two-wheeled robot NXT was realized to evaluate the effect of the following parameters: learning rate α, regularization rate γ, and the universe of discourse of the membership functions. The best parameter values found were: α=0.05 and γ=0.005. The best universe of discourse of the membership functions was -100 to +100. In Figure 9 it is possible to observe the update of the weights through time for these parameters. The addition of regularization ensures a satisfactory performance.

4.5.  PID-NN Control Implementation

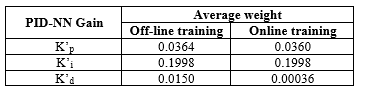
In order to evaluate the proposed algorithm, it was simulated on the Simulink. In this simulation platform several experiments were realized to obtain the best parameter values. The proposed control laws are represented in equations (9-17). Considering the learning rate value α₁=1.0*10^-7, the average weight of the gains obtained to the online and off-line training could be defined in Table 2. The implementation of the online training was developed in Simulink software.

Table 2: Weights of PID-NN off-line training

4.6.  Controllers Performance

The performance of each controlled system was observed for its

1. Stationary balancing on a horizontal flat surface,
2. Balancing during motion at a desired speed on a horizontal flat surface, and
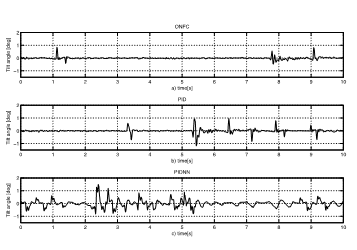
3. Balancing during motion at a desired speed on inclined surface, 10 degrees.The initial valures of inclination angle were assumed zero and the desired speed were set to be 10% of the maximum velocity. The results indicate that the increase in speed and terrain inclination unfavourably affects the performance of the speed control. Figure 10 shows the range of the oscillation of the inclination angle of figure 10 (a) is smaller than plot 10 (b) and 10 (c). Then the error stays close to null value (θ₂=0^o). To quantify the analysis of controllers some comparisons among the integral of plots in Figure 10 is showed in Table 3.Through this calculus get the error between the function of curve and the zero value (equilibrium point). If the value is smaller so the error is smaller. In the case of ONFC, the mean square error in 1200 seconds of the test was of the 0.0172 while for the same interval the PID controller means square error was of the 0.276. Therefore the ONFC control is more stable and it has a better performance for the two-wheeled robot.

 

Table 3: Comparative performance of tilt control in different scenarios

Controller	Error	Flat Terrain		Inclined Terrain
		Stationary	Run	Run
ONFC	MSE	0.0241	0.0302	0.0172
	RMS	0.1562	0.1718	0.0887
PID	MSE	0.0279	0.0276	0.0306
	RMS	0.1663	0.1644	0.1502
PIDNN	MSE	0.0351	0.0266	0.0613
	RMS	0.1883	0.1610	0.2663

Figure 10: Balance control results of tilt control of the two-wheeled robot prototype by employing ONFC, PID, and PID-NN control strategies in inclined terrain.

5.       Conclusion

The ONFC and PID-NN controllers are developed for a two-wheeled robot prototype and they are successfully applied to control the equilibrium of the two-wheeled robot. Compared with conventional PID control schemes, the intelligent controls present better performance, which was verified by experiments. It was verified the effects of terrain inclination in real experiment. The design of such controllers shows versatility, simplicity, improved performance and robustness.

Conflict of Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

1. Deegan, B. Thibodeau, and R. Grupen, “Designing a self-stabilizing robot for dynamic mobile manipulation”, In Proceedings of the Robotics: Science and Systems Workshop on Manipulation for Human Environments, Philadelphia, Pennsylvania (2006).
2. H. Lee, and S. Jung, “Line Tracking Control of a Two-Wheeled Mobile Robot Using Visual Feedback”, International Journal of Advanced Robotic Systems (2013).
3. Su and Y. Chen, “Balance Control for Two-Wheeled Robot via Neural-Fuzzy Technique”, SICE Annual Conference (2010).
4. P. M. Chan, K. A. Stol, C. R. Halkyard “Review of modeling and control of two-wheeled robots”, Annual reviews in control 37: 89-103 (2013).
5. Jin, “Development of a Stable Control System for a Segway,” Royal Institute of Technology (2013).
6. R. Gouvêa, “Controle Neurofuzzy de Motor de Indução Com Estimação de Parâmetros e Fluxo de Estator”, Tese de Doutorado, Programa de Pós-Graduação em Engenharia Elétrica, Universidade Federal de Minas Gerais, Belo Horizonte, MG (2005).
7. V. Pires, “Controladores baseados em técnicas de inteligência computacional: Análise, projeto e aplicação,” Dissertação de Mestrado, Programa de Pós-Graduação em Engenharia Elétrica, Universidade Federal de Minas Gerais, Belo Horizonte, MG (2007).
8. M. Spadini, P. E. Silva, L. F. F. Campos, C. J. F. Araújo, and A, Nied, “Desenvolvimento de Controle Neurofuzzy para Plantas Não Lineares: Aplicação em Tanques Acoplados”, Simpósio Brasileiro Automação Inteligente, SBAI (2013).
9. C. K. Ferrari, “Controlador PID sintonizado por redes neurais artificiais”, Monografia, Curso de Engenharia Elétrica, Universidade Federal do Paraná, Curitiba (2011).
10. R. Bageant, “Balancing a Two-Wheeled Segway Robot”, Thesis (S.B.)-Massachusetts Institute of Technology, Dept. of Mechanical Engineering, (2011).
11. Costa, “A practical implementation of self-evolving cloud-based control of a pilot plant”, in Proceedings of 2013 IEEE International Conference on Cybernetics (CYBCONF 2013), Lausanne, Switzerland, 7-12 (2013).
12. Precup, M. Radac, M. L. Tomescu, E. M. Petriu, S. Preiti, “Stable and convergent iterative feedback tuning of fuzzy controllers for discrete-time SISO systems”, Expert Systems with Applications, 40(1): 188-199 (2013).
13. Castro, R. Carballo, G. Iglesias, J.R. Rabunal, “Performance of artificial neural networks in nearshore wave power prediction”, Applied Soft Computing, 23: 194-201 (2014).

(Click to view)

(Click to view)

No. of Downloads Per Month

No. of Downloads Per Country